2020年度日本大学の過去問を解いたので解答・解説をしていく。
2020年度N方式の全ての問題を解き、文系が大問1〜4、理系が大問5〜10であることには注意してもらいたい。
それでは、早速見ていこう。
問題(大問4)
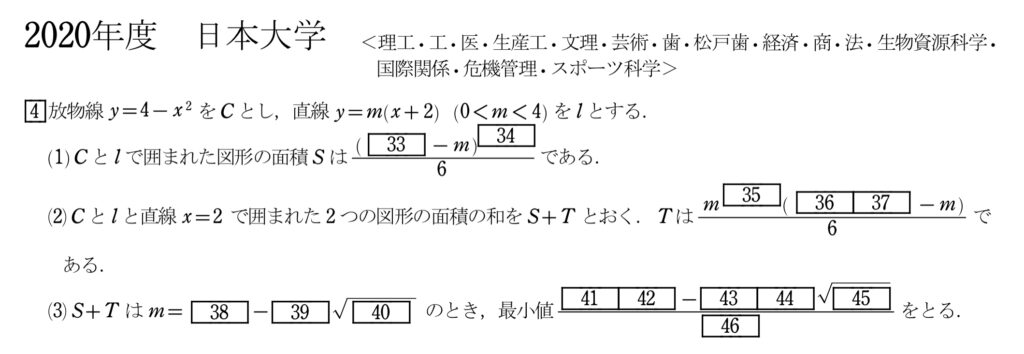
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
日本大学は偏差値35.0〜67.5の私立大学(2021年7月7日時点 パスナビ調べ)。
偏差値自体は35.0の工学部から67.5の医学部まで幅広いため、あまり偏差値はあまり参考にならない。
教科書レベルの基本的な問題だ。
単元も様々で、広く基本的なことができることが問われる。
6乗公式のような積分テクニックを知っていると少し楽ができる。
GMARCH以上や中堅国立を志望する人は基礎力を定着させるためにもしっかり完答できるようにしておこう。
(1)積分
解答
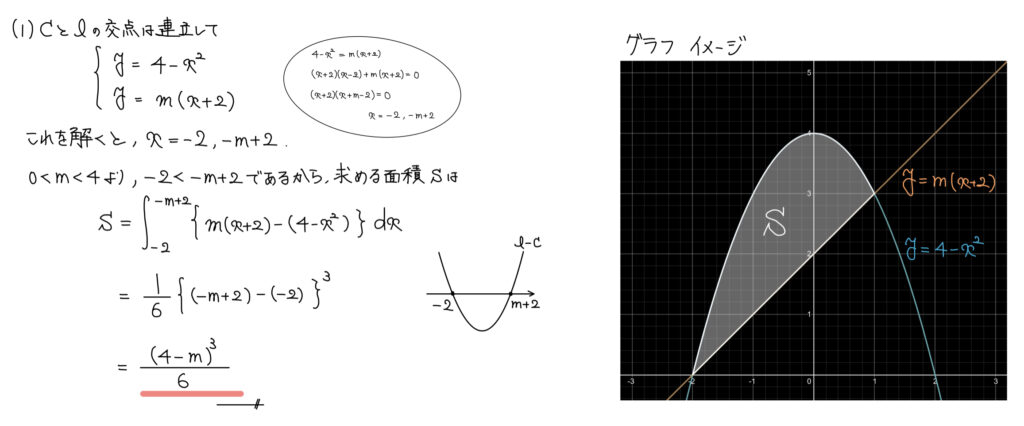
解説
積分に必要なのは関数と区間である。
関数は既に分かっているため、区間を調べれば良い。
区間は交点を調べればよく、交点は連立方程式を解くことで求めることができる。
連立方程式解く→交点分かる→区間分かる→積分できる
ということであとは積分をして終了。
積分は位置関係が「(上の関数)ー(下の関数)」を積分することに注意しよう。
※位置関係が「(下の関数)ー(上の関数)」を計算すると値は同じで符号がマイナスになる
(2)積分
解答
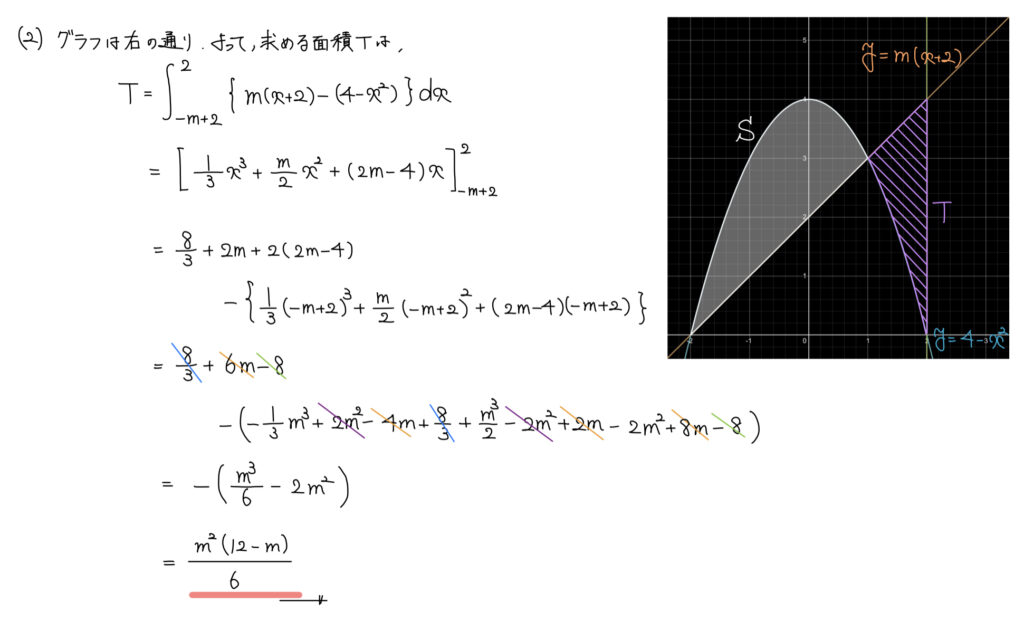
解説
(1)同様、区間を調べて、位置関係が「(上の関数)ー(下の関数)」で積分。
計算ミスに注意しよう。
(3)3次関数の最大・最小
解答

解説
(1)、(2)からS+Tを求める。
あとは最大・最小問題へと頭を切り替える。
3次関数の最大・最小は微分して増減表で処理。
計算ミスだけないように注意しよう。
以下は今回の問題の関数のURL。mの値を動かしながら全体像を把握しよう。
さいごに
微分・積分は特に計算速度と正確性が重要になる。
方針は決まっているので悩むことなくペンが動かせるようになりたいところ。
自分が計算ミスしやすいところを把握して、そういった場面に差し掛かったら注意するという風に自分なりの弱点を把握するとミスが減っていくだろう。
自分は「問題文の見間違え、展開の符号、代入計算」では必ず2回チェックするようにしている。
ミスせず解けるとかなり気持ち良いので、ぜひ体験してもらいたい。
きっと数学が楽しくなりますよ。
これからも頑張っていこう。



コメント