2020年度日本大学の過去問を解いたので解答・解説をしていく。
2020年度N方式の全ての問題を解き、文系が大問1〜4、理系が大問5〜10であることには注意してもらいたい。
それでは、早速見ていこう。
問題(大問5)
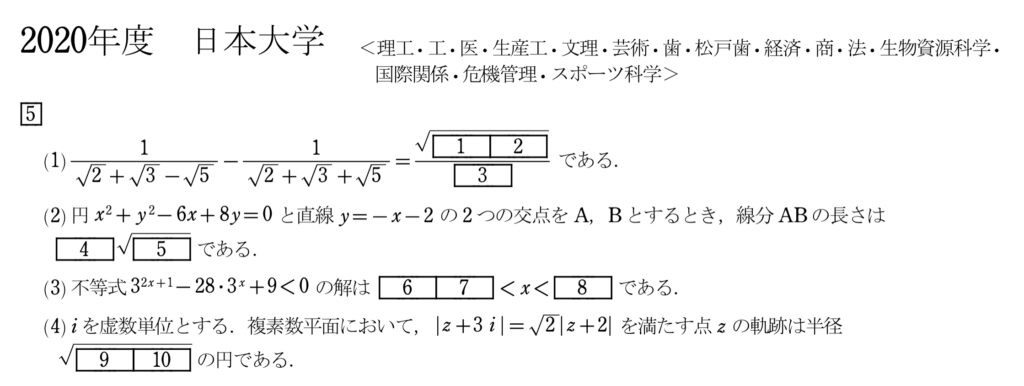
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
日本大学は偏差値35.0〜67.5の私立大学(2021年7月7日時点 パスナビ調べ)。
偏差値自体は35.0の工学部から67.5の医学部まで幅広いため、あまり偏差値はあまり参考にならない。
教科書レベルの基本的な問題だ。
単元も様々で、広く基本的なことができることが問われる。
GMARCH以上や中堅国立を志望する人は基礎力を定着させるためにもしっかり完答できるようにしておこう。
(1)分母の有理化
解答
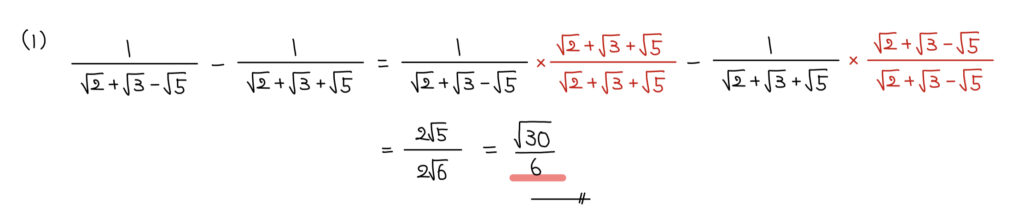
解説
3項の分母の有理化は2項をまとめて1つのカタマリとして見て、2項の有理化として扱う。
2項の分母の有理化は和と差の積の利用。
(2)解と係数の関係、2点間の距離
解答
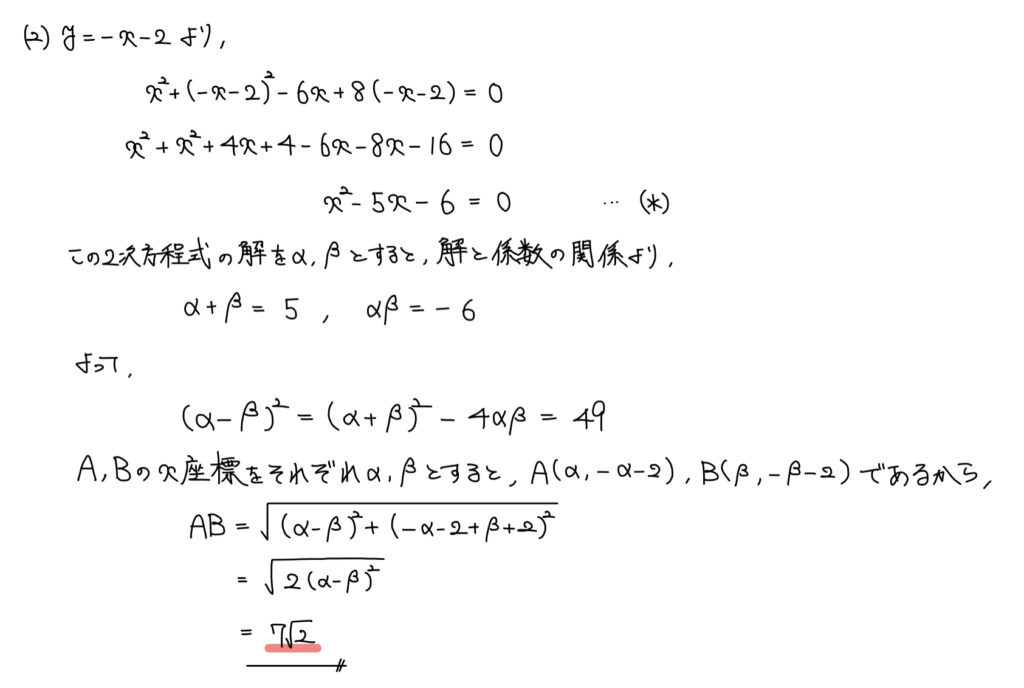

解説
交点を求めるためには連立方程式を解けばいい。
2つの解がそれぞれAとBのx座標に対応するわけだが、どっちの値がどっちの点に対応するかはあまり考えなくても良い。
どっちがAでどっちがBでも距離は変わらないからだ。
どっちでもいいというときは「一般性を失われない」と述べるとよい。
また、最後に求めるものが何かを見据えておくと対称式のアプローチが思い付く。
思い付かなくても解けるが、どちらでも解けるようにしておきたいところだ。
(3)指数不等式
解答
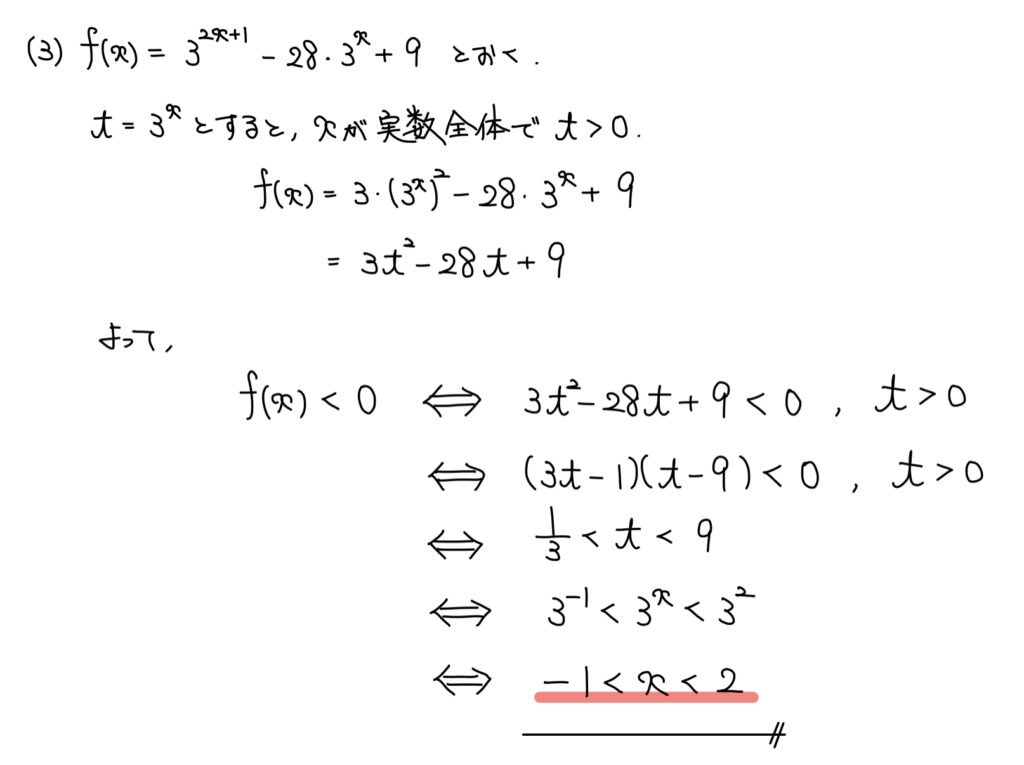
解説
指数方程式は素数の累乗を文字で置いて、整関数へと言い換えるのが定石だ。
文字でおくときは必ず新しい文字の変域に注意することに注意しよう。
今回は2次整関数の不等式へと話を持ち込るため、因数分解で解けばいい。
最後にtからxへ文字を戻してあげれば答えを得る。
(4)複素数と図形
解答

解説
複素数で大きさ同士の等式は2乗して展開していこう。
あとは平方完成のイメージを持ちながら式変形をして行けばよい。
こういった式変形は必ずどの問題集にもある典型問題のため、しっかり抑えておこう。
また、今回は紹介していないが、この問題はアポロニウスの円という有名な図形になる。
興味がある人はぜひ調べてもらいたい。
さいごに
どの問題も教科書の節末問題には載っているだろうくらいのレベルの問題だ。
問題集を持っている人は類似問題があるのではないだろうか。
合格を意識するここで1点も落としたくないところだ。
個人的にはテンプレ計算であまり面白みがなかったが、計算練習には丁度良かったとも思う。
解ける問題を確実に解けることは大事だし、解けた時はしっかり自分を褒めよう。
よくやったぞ、自分。
これからも楽しんでいこう。



コメント