2020年度学習院大学の過去問を解いたので解答・解説をしていく。
今回は経済・法学部の問題を解いた。(理・文学部ではないので注意)
それでは、早速見ていこう。
問題(大問4)

まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
学習院大学は偏差値55.0〜60.0の私立大学(2021年7月21日時点 パスナビ調べ)。
- 「接している」で判別式の反応ができるか
- 「共有点をもつ」で共通解や連立方程式という発想に至るか
- 文字係数の場合分けはできているか
- 積分計算が正しく行えているか
ということを問われているこの問題。
問題としては標準的で、合格者の得点率は高そうだ。
一つ一つの処理は基本知識で、基本知識を有効に使えるか、なぜその解法に至ったのかの部分をしっかり確認していこう。
(1)関数が接する条件、判別式
解答

解説
2つの関数が交点を持つときは
- 連立方程式
- 共通解をもつ
ことを考えよう。
交点を持つ中でも「接する」条件は特殊だ。
連立後、
- 2次関数なら判別式D=0
- 3次以上では因数分解(かならず平方な因数をもつ)
- その他関数では共通接線
を考えよう。
今回は2次関数のため、判別式D=0で解く。
接する関数が2つあるため、2つともで判別式D=0を用いる。
すると、式が2つ、文字が3つで文字を1つまでに減らすことができる。
今回はaを残すよう言われているためb,cを消去すればよい。
(2)2つの関数の共通解
解答

解説
2つの関数の交点のx座標がαとは、すなわち、2つ関数を連立した方程式の共通解がαということだ。
共通解問題は代入で処理しよう。
(3)積分
解答
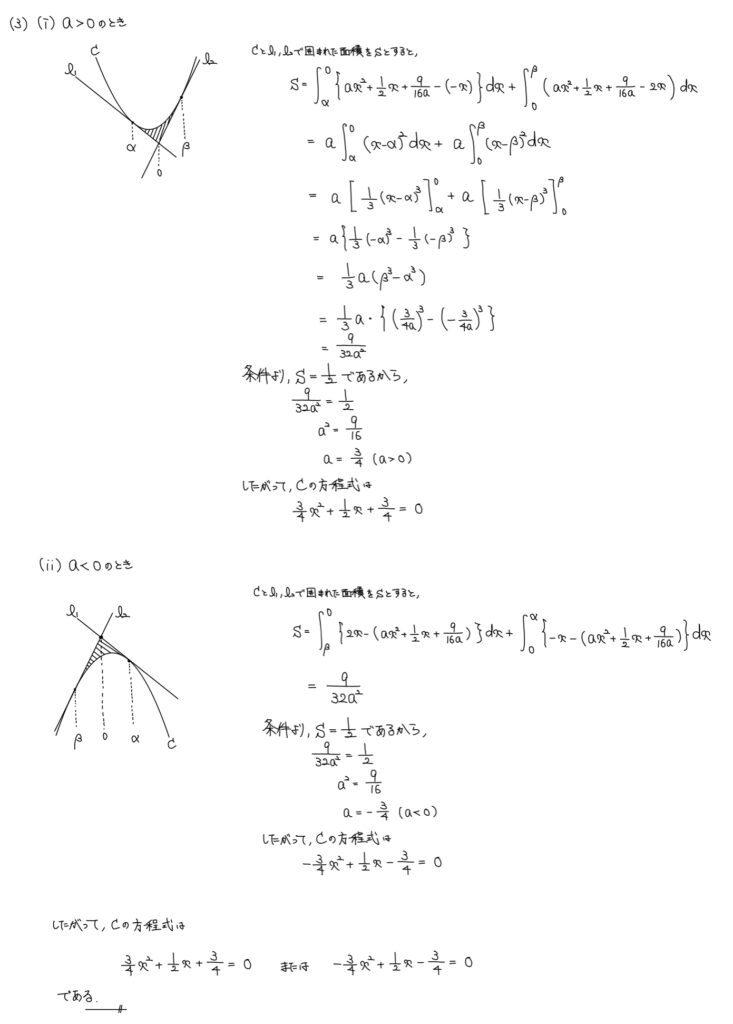
解説
文字係数に慣れていない人はa>0として計算してしまう人が多いだろう。
整関数において、最高次数の係数が文字である時はほぼ確実に場合分けが発生すると思ってよい。
場合分けしてそれぞれ求める面積を積分しよう。
aの正負によって関数の位置関係が異なる。
2つの関数に囲まれた部分を求めるために積分をする際、必ず位置関係が「(上の関数)−(下の関数)」として積分するように注意しよう。
また、今回は用いなかったが、今回の形の積分はは「12分の公式」という公式で知られる有名な形だ。
知っていれば解法に用いることも出来るため知らなかった人は是非調べてみて欲しい。
積分さえ出来れば条件よりaの値を求めて終了だ。
さいごに
流れるように基本事項を確認できる今回の問題。
問題なく解けた人は基本問題をしっかり解けている人だと思う。
今回は特別難しい点もなく、日東駒専志望者も解けるべき問題のように思う。
自分としては楽しみながら解けて良かった。
基本方針が言いながら解けるように練習していこう。



コメント