2020年度北里大学の過去問を解いたので解答・解説をしていく。
今回は獣医学部獣医学科の問題を解いた。(理学部や獣医学部動物資源科学科、生命環境科学科ではないので注意)
それでは、早速見ていこう。
問題(大問5)

まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
北里大学は偏差値40.0〜62.5の私立大学(2021年7月23日時点 パスナビ調べ)。
大問5はベクトルの問題だ。
ベクトルは、図形の単元において位置を気にしない単元である分、比との相性は非常に良く、面積比を考えやすい。(当然相似比、体積比との相性も良い)
そういった点で言えばこの問題は解けておくべき問題のように思う。
面積比はあまり得意でない人が多い印象だが、そんな難しいものでもない。
この問題を通して、ベクトルにおける問題の扱い方をしっかり把握していこう。
大問5(平面の位置ベクトル、面積比)
解答
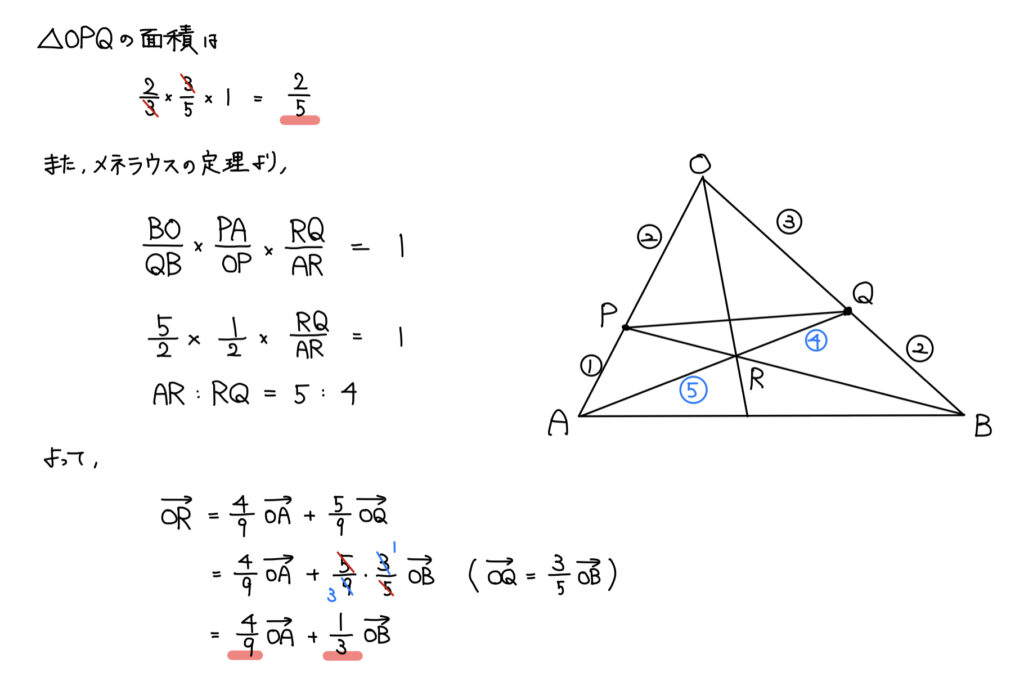
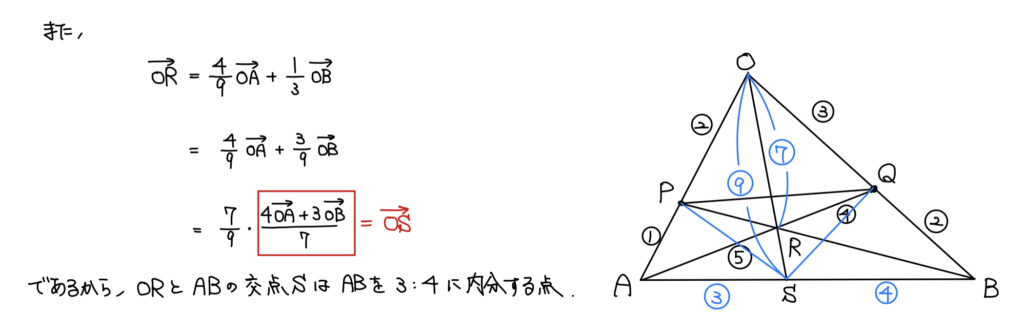
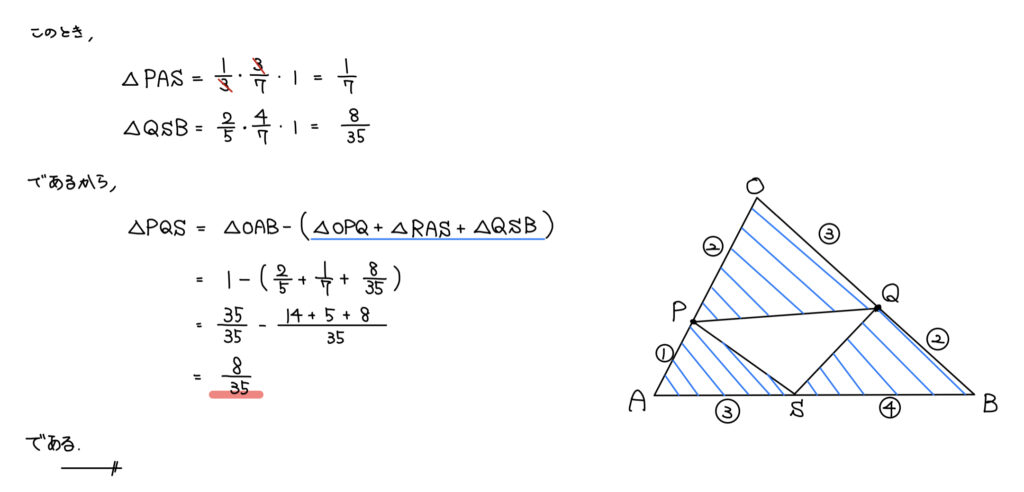
解説
まずは初歩的な三角形の面積比の問題から始まる。
イメージとしては長さが短くなったらその分面積も小さくなると思えば良い。
例えば、Pの位置とQの位置分だけ面積が小さくなるということだ。
その後のRの位置ベクトルについては、「RはAQ上かつBP上」で係数比較でも良いが、メネラウスやチェバ、図形の性質などで比が分かればその方が計算は速くて間違いがないと個人的には思う。
今回はメネラウスの定理を用いてAR:RQの辺の比を求めてRの位置ベクトルを求めた。
その後、Sの位置ベクトルはチェバの定理でも良かったが、せっかくRの位置ベクトルを求めたのでその流れで解いた。
最後の面積については、最初に面積を求めた流れを活用して考えると良い。
自分は解答にあるように、求めたいものだけピックアップした図をかくことが多い。
情報量の寡多で求めたいものを見失わないようにするためだ。
必要なものだけ切り取るようにしている。
さいごに
中学数学をまともに理解していなかった自分にとって、かつて相似比や面積比は大敵であった。
そもそも比という発想が出てこなかったが、受験生になった時にセンター試験対策をしていたら嫌というほど相似比の問題が出てきてできるようになった。
相似比や面積比が苦手という人は、センター試験数学Ⅰ・Aの図形問題だけ解いてみるなども有効なように思う。
ベクトルでは特に比が有効なため、比を扱う発想や問題には慣れていこう。
非常に楽しい問題だった。
これからも頑張っていこう。



コメント