2020年度弘前大学の過去問を解いたので解答・解説をしていく。
今回は理系全般共通の問題を解いた。(理工学部数物科学科の選択問題ではないので注意)
それでは、早速見ていこう。
問題(大問1)
目安時間:25分
2020年度 弘前大学 前期日程 理学部 数学
[ https://nyushi.hirosaki-u.ac.jp/wp-content/uploads/2020/05/R2ze-su2.pdf ]
※上記URL:国立大学法人弘前大学HP 『過去の入試問題』ページより 令和2年度 前期 数学②ⅢB
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。
参考URL『国立大学法人弘前大学HP-過去問題-』https://nyushi.hirosaki-u.ac.jp/faculty/previous-exams/
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
弘前大学は偏差値45.0〜52.5の国立大学(2021年8月1日時点 パスナビ調べ)。
大問1は定積分の計算と回転体の体積の問題だ。
難易度としては(1)、(2)ともに日東駒専〜GMARCHレベルだろうか。
GMARCH合格者の大多数が解けていることが予想される難易度だ。
斬新な発想は必要なく、基礎知識と計算力が求められている問題と言える。
全体的に日東駒専で扱わないような少し難易度高めの基本知識が求められるわけだが、それは弘前大学なら当然と言える。
弘前大学志望者であればここは確実に正解しておきたい。
(1)定積分
解答
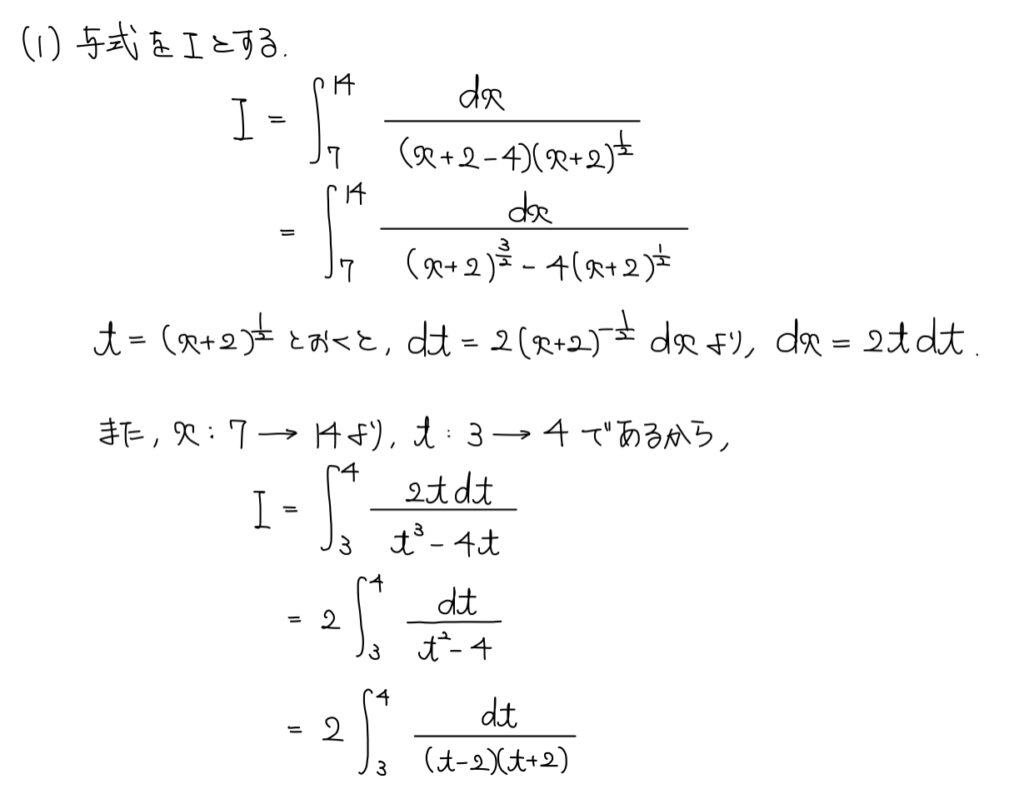

解説
今回問題を見て明らかなのが
- 平方根を含む
- 分数式
の形であることだ。
まずは平方根の処理からしよう。
平方根の基本処理は丸ごと置換することだ。
平方根の部分含めて丸ごと t とおこう。
これで平方根に関しては処理を終え、次に分数式の形を処理しよう。
分数式型の積分計算で考えたいのがlogをとる形か部分分数分解だ。
今回は部分分数分解で解いていけばよい。
部分分数分解によって得た分数式の形は迷わずlogを取ることで解答を得る。
(2)回転体の体積
解答
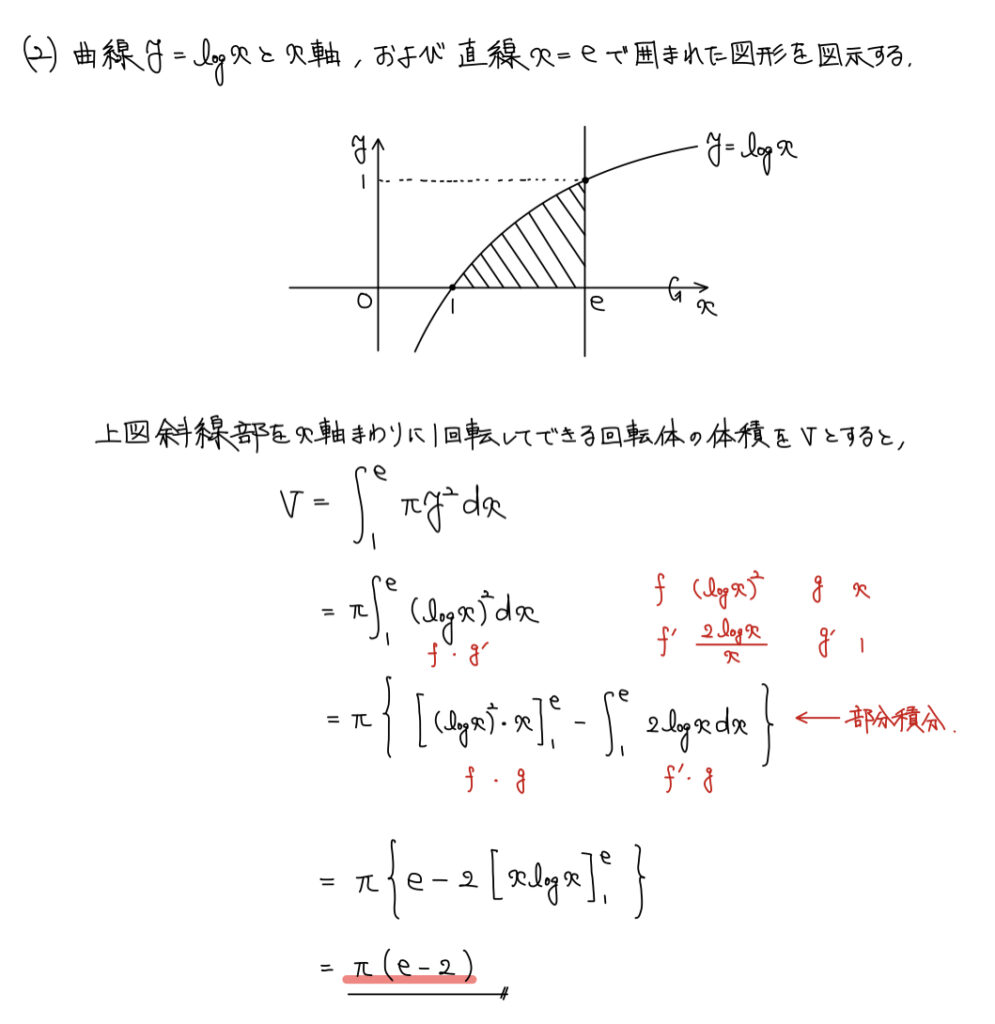
解説
回転体の体積を考えるにあたり、どこで囲まれた図形をx軸周りに回転させるのか図示して確認しよう。
図示して確認した後は基本通りに回転体の体積を求めよう。
基本的な問題ゆえここでの得点は必須なため、計算ミスだけには十分注意しよう。
さいごに
公式の模範解答はこちら
https://nyushi.hirosaki-u.ac.jp/wp-content/uploads/2020/05/R2ze-su2_kaitou.pdf
参考URL:国立大学法人弘前大学HP 『過去の入試問題』ページより令和2年度 前期 数学②ⅢB 解答例
やはり全体的に求められる基礎力は高い。
公式を利用するだけで即座に解答という問題はない。
とはいえ、問題集を1冊終えた人なら見た事ない問題というのはないはずだ。
また、計算力を問われる大問1のため、時間掛かりそうだな〜と思ったらいち早く次の大問にいってしまおう。
後日大問2、大問3と執筆していくが、大問3つで90分はまずかからない。
ここで大問1を後回しにしたとしても余裕で戻って来られるだろう。
個人的には半分の45分でも結構余裕があるように思える。
どう解くかに方針に悩むというより、計算力に手が掛かる問題が多いため、計算は迅速かつ正確に解く練習を積んでおく必要がある。
初めて解いたが久々に計算をゴリゴリしたな、という感想だ。
楽しい問題だった。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント