2020年度岩手大学の過去問を解いたので解答・解説をしていく。
今回は前期・理工学部の問題を解いた。(理工学部以外の学部や後期の問題ではないので注意)
それでは、早速見ていこう。
問題(大問1)
目安時間:20分
2020年度 岩手大学 前期日程 理工学部 数学
[ https://www.iwate-u.ac.jp/upload/images/032.rikou_sugaku.pdf ]
※上記URL:国立大学法人岩手大学HP 過去問ページより 2020年度 前期日程 理工学部数学
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。
参考URL『国立大学法人岩手大学HP-過去問題-』
https://www.iwate-u.ac.jp/admission/disclosure/past.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
岩手大学は偏差値45.0〜60.0の国立大学(2021年8月1日時点 パスナビ調べ)。
大問1は様々な単元の小問集合の問題だ。
具体的には
- (1)関数の極限(数Ⅲ)
- (2)2直線のなす角
- (3)指数対数の不等式
- (4)確率の加法定理
が並んでいる。
難易度としてはGMARCHレベルだろうか。
とはいえ、(4)が飛び抜けて簡単であるため、ここは落とせない。
(1)〜(3)も解けない人はいそうだが基本問題ではある。
小問集合のため、誘導はない。
ゆえに解法には悩まず、時間をかけずにどんどん解いていきたい。
それでは実際に解答を見ていこう。
(1)関数の極限
解答

解説
まずxを∞に飛ばすと「∞ – ∞」の不定形となる。
根号を含む不定形は有理化を考える。
有理化をした後は分母の発散が一番強いもの(分母の最高次数)で分母分子を割れば良い。
(2)2直線のなす角
解答

解説
2直線のなす角は
- 直線の傾き(tanθ)の利用
- 法線ベクトルの利用
をすぐに思い付くようにしたい。
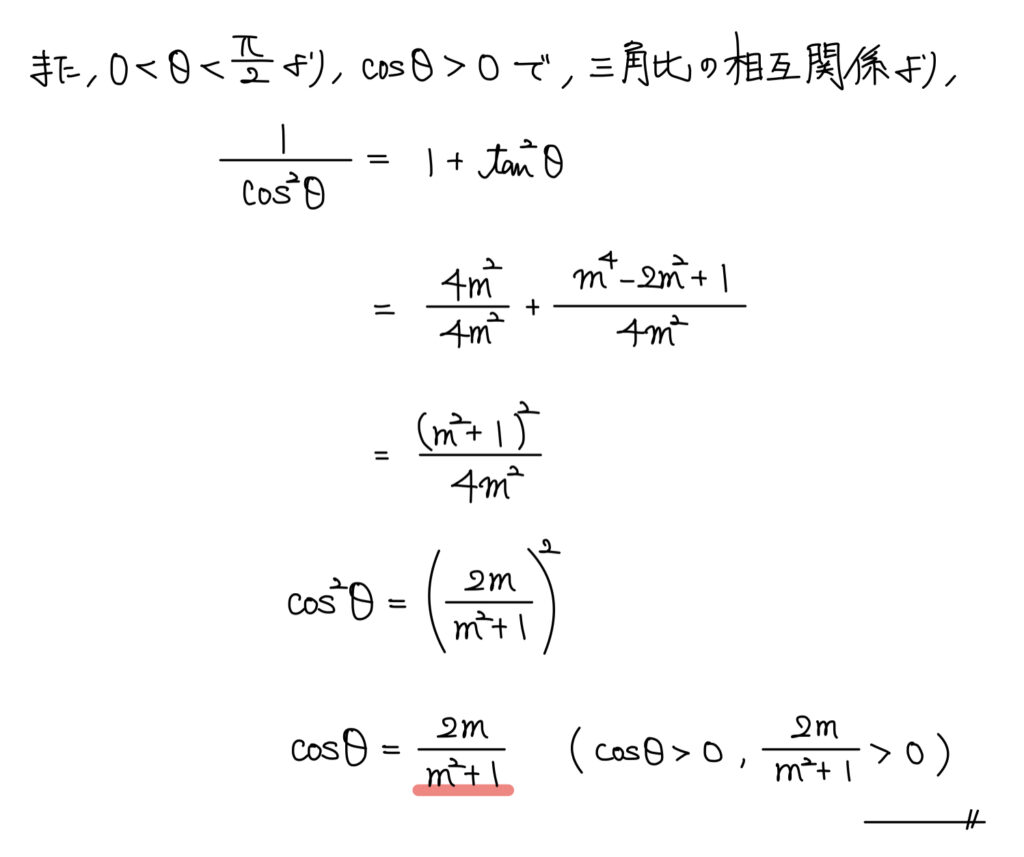
今回は「なす角を求めたい」というより「なす角を使った三角比を求めたい」というのがゴールのため、法線ベクトルではなく傾きの利用で求めよう。
tanが求められた後は三角比の相互関係から求めよう。
(3)指数対数の不等式
解答

解説
ゴールは「不等式を満たす最小の自然数を求める」ということから「n>●」という形を目指すことが分かる。
今、nが指数部分にあるため対数をとって指数部から下ろしてあげよう。
今回は問題文で真数が3の常用対数が用意されているため、常用対数を取ることにしよう。
後は間違いないように計算していけば良い。
(4)確率の加法定理
解答

解説
「赤玉の数が白玉の数より多い」というところから余事象を考えることもできる。
今回の解答は余事象ではなく直接求めることで解いた。
排反事象より確率を足して結論を得る。
さいごに
公式の模範解答はこちら
https://www.iwate-u.ac.jp/upload/images/050.zenki_kaitourei_2.pdf
参考URL:国立大学法人岩手大学HP 過去問ページより 2020年度 前期日程 解答
程良い難易度で個人的には大問1であってくれるのが嬉しい。
ここで勢いをつけてこの後の大問もズバズバ解いていきたいところだ。
他の大問に比べて易しいため、ここでちゃんと得点を取っておきたい。
楽しい問題だった。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント