2020年度岩手大学の過去問を解いたので解答・解説をしていく。
今回は前期・理工学部の問題を解いた。(理工学部以外の学部や後期の問題ではないので注意)
それでは、早速見ていこう。
問題(大問2)
目安時間:20分
2020年度 岩手大学 前期日程 理工学部 数学
[ https://www.iwate-u.ac.jp/upload/images/032.rikou_sugaku.pdf ]
※上記URL:国立大学法人岩手大学HP 過去問ページより 2020年度 前期日程 理工学部数学
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。
参考URL『国立大学法人岩手大学HP-過去問題-』
https://www.iwate-u.ac.jp/admission/disclosure/past.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
岩手大学は偏差値45.0〜60.0の国立大学(2021年8月1日時点 パスナビ調べ)。
大問2は楕円と接線・法線、それらで囲まれた部分の面積の問題だ。
難易度としては日東駒専以上GMARCHでは易問といったレベルだろうか。
問題自体はかなり基礎的なことを問いているような問題ではあるが、楕円というテーマが正答率を下げているといった感じだ。
(1)が解けている人はその後も順調に解けていそうな問題であるため、(1)を解けるかどうかというのが大きな分かれ目になりそうだ。
楕円は避けがちなテーマではあるが、中堅〜難関と言われる大学ではよく扱われるテーマではある。
ここでしっかり復習しておこう。
それでは解答を見ていこう。
(1)楕円の接線
解答

解説
接線の方程式は多くの人が知っているだろう。
だが、楕円と言われると悩んでしまう。
その理由として、いつも扱っているのは y が1次であるのに対し、楕円は y が2次であることが挙げられる。
楕円というだけで苦手と感じる人は多いと思うが、実はやっていることは全く同じで「xで微分して接点を代入したものが接点における傾き」ということだ。
その際に y は x の関数であることから、合成関数の微分をすれば良い。
その後は分かりやすいように y’= の形を作れば良い。
(2)法線の方程式
解答

解説
(1)で接線の傾きが分かるため、法線の傾きは直ちに求められる。(傾きの積が -1 )
あとは法線の方程式の通りに記述すれば良い。
(3)分数式の最大・最小(相加・相乗平均)
解答


解説
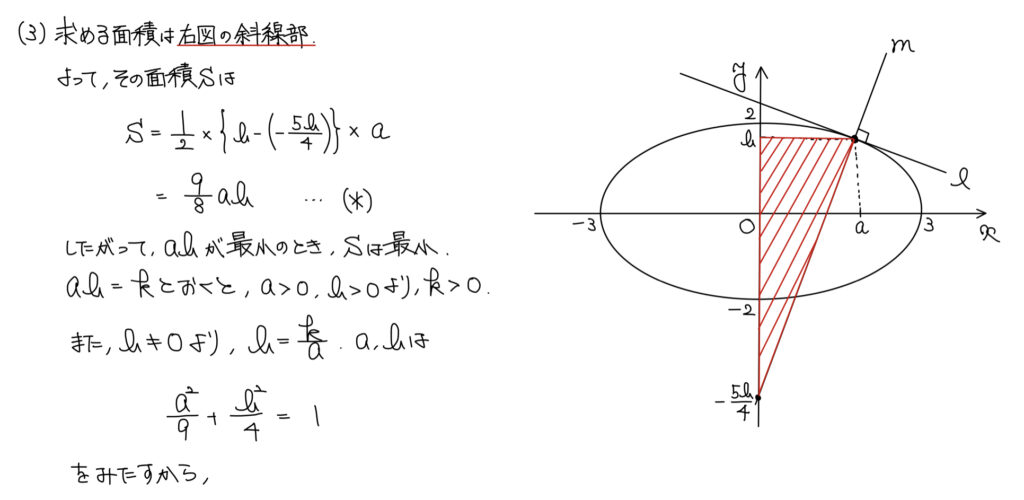
求める面積をまずは図をかいて確認。
すると三角形であることが分かるため、面積自体は9ab/8といった形で求めることができる。
ここでabの最大・最小を考えていくという流れになるが、ここで考えるのがaとbの2変数関数の最大・最小問題だということだ。
多変数関数の最大・最小問題の解法パターンは以下の通りだ。

一つ一つの詳細はここでは書かないが、今回有効なのが逆像法だ。
逆像法とは、簡単に言えば「=kとおいてkの存在範囲を求める」というものだ。
今回はab=kとおき、kがどのような範囲にいるかを考えていく。
kをa,bの式と合わせて最大・最小を求めていく。
解答の通り式変形をしていくと最終的に4次関数の最大・最小問題へと落ち着くため、求めることができるということだ。
その際に、a,bの取りうる範囲には十分に注意しておこう。
そうでなければkが取れないはずの値を取ってしまう可能性が出てくるからだ。
何を求めたくてどんな作業をしているのか見失わないように気を付けよう。
(3)【別解】相加・相乗平均
解答

解説
他変数関数の最大・最小問題の処理として、有名不等式の利用というものがある。
その内の一つが相加・相乗平均だ。
知っているけど使えない公式ランキング上位であろうこの不等式。
今回相加・相乗平均で解答を作成するとこんなにもあっさり記述できてしまう。
では、どう考えたら相加・相乗平均の利用に至るかだが、ポイントは楕円の式が2乗の和で記述され、求めるものがabという積であるということだ。
和と積の形を確認したら相加・相乗平均が有効であることがある。
そのため、和の最小や積の最大を見たら(ん?もしかして相加・相乗平均使える?)という気付きがあると良い。
相加・相乗平均は2つの数が正の時にしか用いることができないのでその点には注意しよう。
さいごに
公式の模範解答はこちら
https://www.iwate-u.ac.jp/upload/images/050.zenki_kaitourei_2.pdf
参考URL:国立大学法人岩手大学HP 過去問ページより 2020年度 前期日程 解答
正直自分は楕円が苦手だ。
だからこそこの問題を解いて良かったと思う。
面積の最大・最小も、正直最初は相加・相乗平均に気付かなかった。
後から見直せばそれはそうとなるが、こういったところで気付けないのは悔しい。
この問題は難易度こそそんなに高くはないものの、色々学べることは多い良い問題だった。
個人的には定期的に解いてみたい問題だった。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント