2020年度岩手大学の過去問を解いたので解答・解説をしていく。
今回は前期・理工学部の問題を解いた。(理工学部以外の学部や後期の問題ではないので注意)
それでは、早速見ていこう。
問題(大問4)
目安時間:20分
2020年度 岩手大学 前期日程 理工学部 数学
[ https://www.iwate-u.ac.jp/upload/images/032.rikou_sugaku.pdf ]
※上記URL:国立大学法人岩手大学HP 過去問ページより 2020年度 前期日程 理工学部数学
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。
参考URL『国立大学法人岩手大学HP-過去問題-』
https://www.iwate-u.ac.jp/admission/disclosure/past.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
岩手大学は偏差値45.0〜60.0の国立大学(2021年8月1日時点 パスナビ調べ)。
大問4は図形と方程式の問題だ。
難易度としては日東駒専以上GMARCH未満といったところだろうか。
すべての大問が基本的なレベルで、(3)は原点を通る直線OPの傾き(正三角形)が見えたかどうかで決まる。
二等辺や有名角が与えられたら初等幾何の登場かもしれないとアンテナを張っておくことが重要だ。
それでは解答を見ていこう。
(1)2点間の距離
解答

解説
「2点間の距離が等しい」というのが問題の状況。
2点間の距離は三平方の定理によって導かれる。
座標や成分の公式を覚えてもいいが、それらをいちいち覚えていなくても「2点間の距離は三平方の定理」で理解してしまった方が色々な問題や状況に応用が効く。
座標でもベクトルでも複素平面でも、全て2点間の距離は三平方の定理だ。
また、距離が等しい時に平方根が出てくるのが嫌なため、あらかじめ2乗しておくと良いだろう。
この手の式変形は問題集にもよく載っているためよく知られているが、ひとつだけ注意しておきたいことがある。
それが「距離だから両方正の数」という条件だ。
正負のどちらの実数も、2乗すると必ず正になる。
ゆえに2乗した値が等しいからって元の数が等しいとは限らないということだ。
例えば-2と2は異なる数であるが、2乗すればともに4になる。
ゆえに、「2乗した数が等しいから元の数が等しい!」とはならないことがあるため注意が必要だ。
「両方正の数」という条件がつけばマイナスが除外され、「2乗した数が等しいから元の数が等しい!」と言える。
解答の「OP>0 , OQ>0より」という一言は必ず入れる癖をつけていこう。
(2)軌跡の方程式
解答

解説
軌跡の方程式の基本処理は
- 求める点を(X,Y)とおいて媒介変数表示
- 媒介変数の存在条件を求める
という手順で求められる。
まず求める点を(X,Y)ということは有名解法なため出来ている人が多いのではないだろうか。
分からなかった人もここで学べば差は埋まったのだから気にする必要はない。
その後の「媒介変数の存在条件を求める」というところで(ん?)ってなる人はいるのではないだろうか。
軌跡を学習した人で多いのが「媒介変数(文字)の消去をすればいい」と覚えているパターンだが、これは合っているが本質的ではない。
媒介変数の消去ができる問題では有効だが、実は媒介変数の消去をしても存在条件に注意する問題や、そもそも媒介変数の消去がうまくできない問題は沢山ある。
こういった時に意識したいのが媒介変数の存在条件を求めるということだ。
今回文字消去としか考えなかった人の解答には最後に(x>0)の記述がないのではないだろうか。
逆に、媒介変数の存在条件を意識している人の解答には当たり前に(x>0)の記述がある。
これは媒介変数tがどの範囲で存在しているかに目を向けられているか否かの差だ。
tに範囲があって、tとxに関係(式)があるのであれば当然xにも範囲がある。
それは実数全体という範囲かもしれないし、開区間や閉区間など範囲は様々だ。
今回はtが0より大きいという存在条件からxの存在条件を求めた形になる。
今回の問題では存在範囲について詳細に説明することはできなかったが、これからも必ず媒介変数の存在する範囲がどこかということには目を向けていって欲しい。
媒介変数tの存在条件を確認したら、XとYの関係式からtを消去して結論を得る。
(3)平面ベクトルの内積
解答

解説
まず、条件から△OPQが正三角形であることに気付きたい。
多角形に関する問題では辺と角の情報が何よりも重要になる。
辺と角さえ求めてしまえば多角形の解答は見えてくる。
今回のように多角形問題が座標で与えられることもあるが結局重要なのは辺と角だ。
座標というのは点に住所を与え、点と点の距離、すなわち、辺の長さを考えられるようにしたものだ。
辺の長ささえ分かれば別に座標は必要ではない。
ゆえに、多角形の問題を見たらまず辺と角の情報を探しにいくのだ。
そういった意味で、今回の正三角形のような辺の長さも内角も全て分かるような図形は非常に扱いやすい。
正三角形に気付くと60°の角の条件に目がいく。
辺の長さは t が入ってきてしまい不確定要素が多いからだ。
ここまで分かれば「平面上の3点(平面図形)」、「座標(成分)」、「辺のなす角」という条件からベクトルで解けそうという発想になるのではないだろうか。
ベクトルの発想に至ったらもう安心で、「ベクトルで角度問題」と言えば必ず「内積処理」だ。
「成分での内積」と「大きさとなす角の内積」の等式で結論を得る。
【別解】(3)傾きの利用
解答
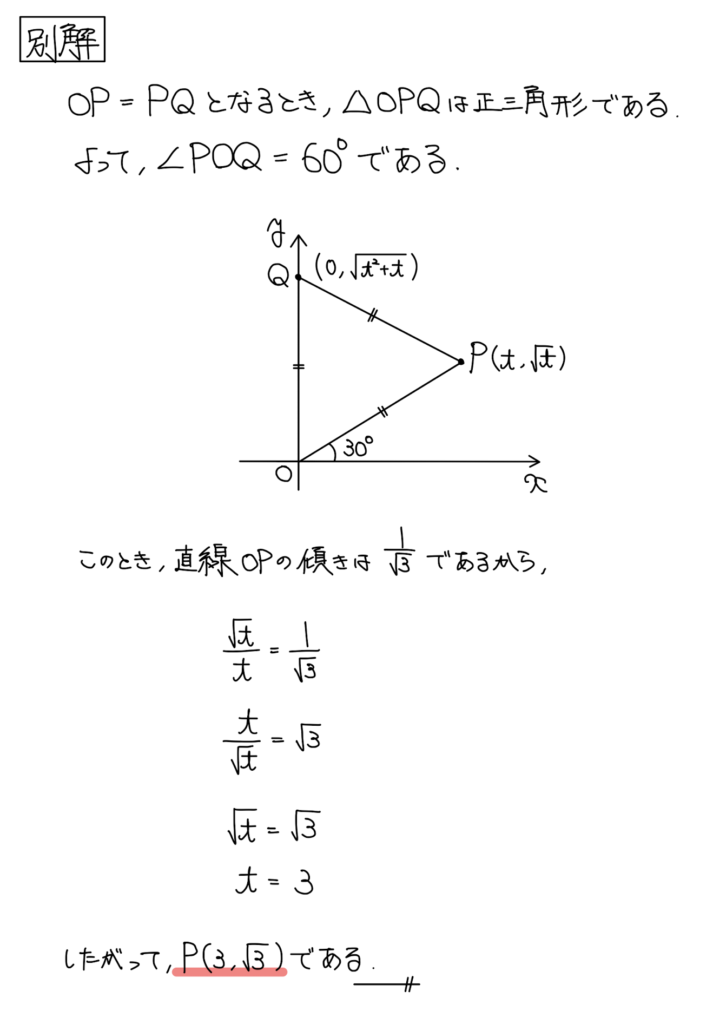
解説
問題を簡単に把握するために図示した人は解答のような図をかいているだろう。
ここで、正三角形であることに気付くと直線OPの傾きが分かる。
この傾きの発想は「原点」であることと「有名角(60°)」であることから考えられる。
(tan60°から連想もできる)
あとは傾きに着目して立式すれば解答を得る。
さいごに
公式の模範解答はこちら
https://www.iwate-u.ac.jp/upload/images/050.zenki_kaitourei_2.pdf
参考URL:国立大学法人岩手大学HP 過去問ページより 2020年度 前期日程 解答
ベクトルの問題をベクトルとして解ける人は多いが、ベクトルとして与えられていない問題をベクトルを扱って考えるという発想がない人は多くいるだろう。
基本的にベクトルは処理が数式による処理が可能なため、図形問題が苦手な人こそ考えたい武器の一つだ。
今までに学んだ様々な図形問題を今一度(なぜこの問題はベクトルで解かなかったのだろう)、(この問題ベクトルで解けないかな?)と考えてみるとベクトル問題として扱うかべが壊せそうだ。
図形問題が苦手(補助線とかが特に苦手)なため、常にベクトルで考え数式処理をしている。
補助線のような賢い発想が必要ない分計算が大変なこともあるが、逆に言えば計算さえできればベクトルは発想なしで解ける。
いわば天才発明家と戦うための凡人の地道な努力のようなものなのだ。
だからこそ自分はベクトルが好きだ。
図形が苦手な人ほど一度ベクトルに浸かってみて欲しい。
ベクトル楽しいよ。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント