2020年度秋田大学の過去問を解いたので解答・解説をしていく。
今回は前期日程の問題を解いた。
大問自体は全学部9題ある用紙を配布されるが、そのうちどの大問を選択して解答するかは学部学科によって異なるため注意して欲しい。
学部ごとにどの大問を選択すれば良いかは以下画像の赤枠内参照。

それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『秋田大学 過去問』で検索してみて欲しい。
目安時間:15分
2020年度 秋田大学 前期日程 数学
[ https://www.akita-u.ac.jp/honbu/exam/pdf/r2_zenki/r2zenki_05.pdf ]
※上記URL:国立大学法人秋田大学HPホーム > 入試情報 > 過去問題 > 令和2年度 > 前期日程 > 数学
※過去8年分が公式HP(下記URL)から閲覧できます。(2021年8月18日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人秋田大学HP>入試情報>過去問題』
https://www.akita-u.ac.jp/honbu/exam/ex_pastissues.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
秋田大学は偏差値42.5〜62.5の国立大学(2021年8月18日時点 パスナビ調べ)。
大問1は様々な単元の小問集合だ。
難易度はかなりばらつきがあるが、(1)は日東駒専未満、(2),(3)は日東駒専レベルだろうか。
全体としてはどの学部も大問4つで試験時間90分。
大問1問を22分程度と思うと、大問1は15分くらいで駆け抜けたいところ。
(といっても別に後半の大問でも時間的に余裕のある問題もある)
問題自体は小問らしく、問題集にそのまま載っていてもおかしくない問題である。
時間を考えた時に、(2)は合同式を用いないと長い解答(別解)になってしまうため、余力があれば合同式も押さえておくといいだろう。
合同式を用いないと決めている人は、解法に迷わずちゃきちゃき手を動かせるような問題なれはしておきたい。
それでは解答を見ていこう。
(1)独立な試行の確率
解答

解説
場合の数、確率において問題文で指定されたものは先に考えると良い。
今回は「6回目で初めて6が出る」と6回目に指定が入っているため、6回目とその他で分けて確率を求めよう。
計算は方法については、独立な試行の確率の通り、各回の確率の積で求められる。
(2)指数型の余り
解答
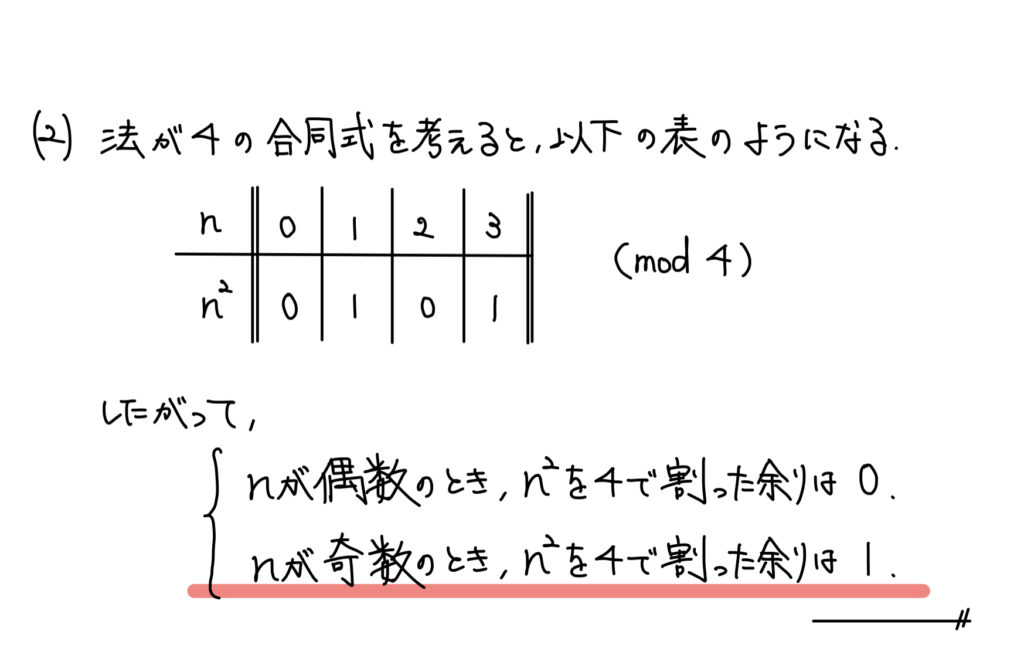
解説
指数型の余りは以下の手順で求めることができる。

今回は4で割るため、4を互いに素な法に分解するのだが、そもそも4は22のため特に分解などはしなくて良い。
(例えば「12で割った余り」という問題なら、法を3、4とそれぞれ互いに素な法に分けて余りを調べることになる)
ゆえに、今回は純粋に4を法とした余りを考えれば良い。
割る数が文字nでよく分からないため、場合分けしてもいいが表にまとめた。
あとは解答の通り。
【別解】(2)指数型の余り
解答


解説
合同式を習ったことのない・知らないという人はこちらの解法になる。
別解と書いているが、本質的行っていることは変わらない。
nを4で割った余りを調べたいが、nが文字のせいで余りが0〜3のどれか分からない。
では、それぞれの場合に分けて考えていきましょう、という流れ。
あとは解答の通り。
書いている途中である程度推測ができるため、書きながら(結論はこう書こうかな)なんて考えても良いかもしれない(計算ミスには十分に注意が必要)
(3)an+1=pan+f(n)型の漸化式
解答


解説
「an+1=pan+f(n)型の漸化式」は「an+2-an+1をして階差型へ」という解法の方針で解答を得る。
どの問題集にも載っているであろうテンプレ漸化式の形ではあるが、この型をしっかり解けている人が何人いるかは疑問だ。
そんな誰しもが解ける問題ではないように思う。
大問1はこの(3)が解けたかどうかで上位陣とそれ以外で振り分けされるだろう。
階差型を発見した時点で、あとは階差数列の漸化式の解法だ。
「初項+階差の1から(n-1)項までの和」でいいだろう。
ここで必ずn≧2の条件は必須。
あとはn=1を調べて解答を得る。
時間に余裕があればn=2,n=3と代入して確認しておこう。
さいごに
(1)から(3)に進むにつれて難易度が上がっていく。
とはいえ、全部市販の問題集からそのまま引っ張ってきたと言ってもいいような問題のため、ここは確実に正解しておきたい。
(3)が解けなかった人はそう落ち込まず、今ここで確認できたし、全員が解けてるわけじゃないからよし!と思っておこう。
(1),(2)の計算ミスには注意しよう。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント