2020年度神戸大学の過去問を解いたので解答・解説をしていく。
今回は前期日程(理科系)の問題を解いた。
文科系の問題ではないことには注意してもらいたい。
それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『神戸大学 過去問』で検索してみて欲しい。
目安時間:18分
2020年度 神戸大学 前期日程 数学
[ https://www.office.kobe-u.ac.jp/stdnt-examinavi/wp-content/uploads/2020/08/03.suugaku_rikei.pdf ]
※上記URL:国立大学法人神戸大学HPホーム > 入試情報 > 学部入学案内 >入試問題及び出題の意図など > 2020年度一般入試(入試問題/出題の意図・評価ポイント/解答例)> 前期日程 数学 理科系 問題
※過去4年分が公式HP(下記URL)から閲覧できます。(2021年8月29日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人神戸大学HP>入試情報>学部入学案内>入試問題及び出題の意図など』
https://www.kobe-u.ac.jp/admission/undergrad/examin/index.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
神戸大学は偏差値55.0〜67.5の国立大学(2021年8月30日時点 パスナビ調べ)。
大問1は剰余の定理と領域についての問題だ。
難易度は日東駒専以上GMARCH以下の問題だ。
解けたかどうかはさておき、すべての小問において方針決めが分かりやすい問題であることは間違いない。
方針が分かる以上はその通りに解いていくのだが、それをしっかり解答に落とし込めるようにしていこう。
それでは解答を見ていこう。
(1)剰余の定理
解答

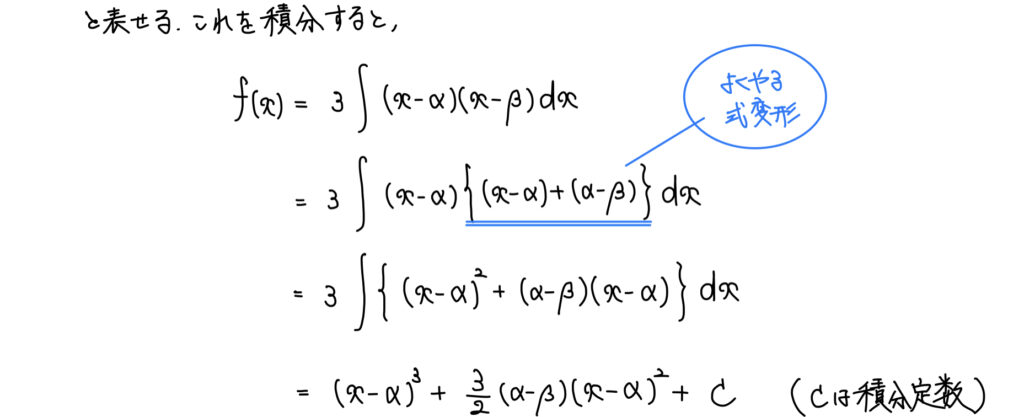
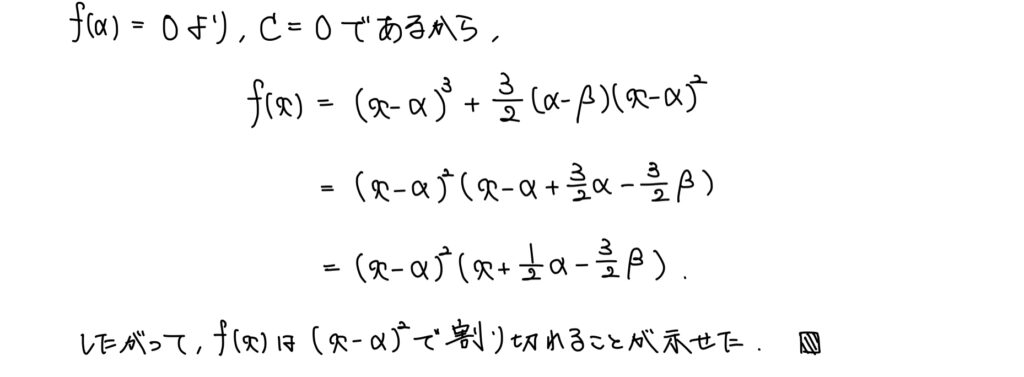
解説
自分がこの問題を見た時に思ったのが「f(x)=x3+ax2+bx+cとおこうかな」だったが、すぐにやめた。
条件が2つで変数を3つ設定しても求められないからだ。
そこですぐに関数自体を求めることは厳しいことに気付いた。
方針を変えて、3次式より2次式の方が考えやすいため導関数f’(x)から考えた。
また、(2)でf’(x)=0が見えていたため、この形が後々便利かなとも考えた。
あとは剰余の定理と不定積分をすれば求めることができる。
自分はこの解答だったが、別解の方が一般的な解答と思われるためそちらも確認してもらいたい。
【別解】(1)剰余の定理
解答

解説
この記事では別解扱いだが、一般的な解答はこちらのように思う。
関数f(x)を求めようとするのではなく、あくまで(x-α)2で割り切れることのみ示せばいい。
あとは剰余の定理を順に使っていけばいい。
(2)剰余の定理
解答

解説
(1)からf(x)の形だけは分かるため、βを求めにいった。
計算自体は1次方程式のため解説も不要だろう。
また、別解で解いた方もf(α+2)=0より、f(x)=(x-α)2{x-(α+2)}を得る。
あとは微分してf’(x)=0を満たすαでないxを求めればよい。
(3)関数の領域、定積分
解答

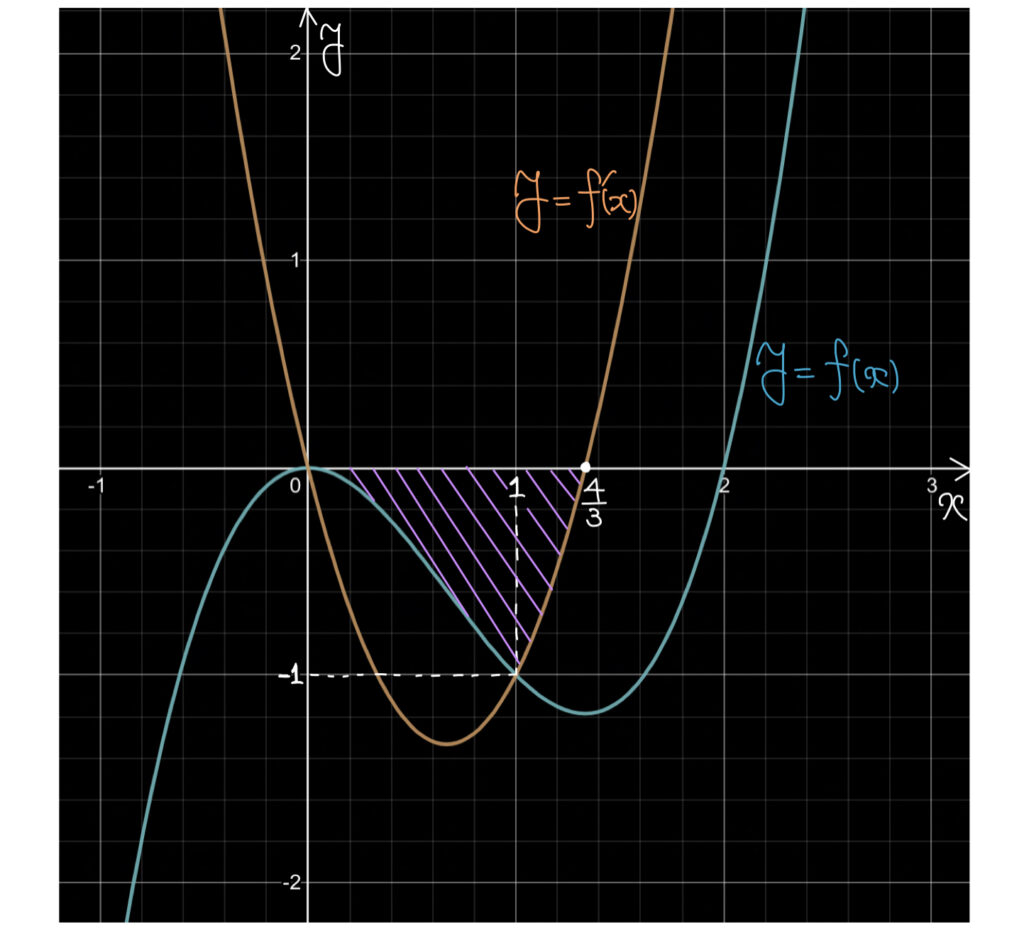

解説
関数が分かるため、あとはグラフをかいて上下関係を把握しよう。
上下関係を把握したら求める領域を図示して積分。
計算ミスをしないように気をつけよう。
さいごに
剰余の定理と領域、定積分についての基本問題だった。
入試問題特有の現象として「出題のされ方の違いで方針決めが分かりづらい」というのがあると思うが、いかに自分の知っている出題形式として解釈できるかというのがあるように思う。
「これってこういうこと言ってるよね」と条件や解答までの方針を抽出して自分の中で整理できるようにしていこう。
解いた方お疲れ様でした。
これからも一緒に頑張っていきましょう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント