2020年度 小樽商科大学の過去問を解いたので解答・解説記事をしていく。
早速見ていこう。
問題(大問1)
※現在問題は非公開とさせていただいております。
過去問題は大学公式の問い合わせホームから直ちに請求できます。
費用もかかりませんので是非行ってみてください。
年度により請求できないものもあります。
公式サイト『国立大学 小樽商科大学 受験生サイト-過去問題請求ホーム』
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
全体概評
小樽商科大学は偏差値50の国立大学(偏差値はパスナビ調べ)。
難易度としては難問ではなく、典型的な問題と処理で解ける。
大問1は小問3つで構成されている。
単元は様々で(1)空間座標、(3)積分方程式は受験生が苦手そうな範囲ではありそうだ。
そこまで難しくはなく、問題文に惑わされず基本通りの処理と計算をしっかりしていけば完答できる。
(1)直線の方程式
解答

解説
x,y,z軸からなる空間において2点が与えられ、2点を通る直線を考えるというところから問題は始まる。
その後、座標が文字定数の通る2点を与えられ、その2点の中点を求めるといった問題。
「通る2点→代入可能」という発想から直線の方程式を考えることになるが、その際に方針は数Ⅱの直線の方程式(①)と数Bの空間ベクトル(②)どちらでアプローチしようかと瞬時に引き出せるようにしておきたい。

自分は①でのアプローチで示した。方針さえ決まれば後は「yz平面上ってことはx成分0」や「中点は2点座標の平均」といったような簡単な処理で解ける。
最初の方針決めだけ把握しておけば解ける問題だ。
(2)指数・対数方程式
解答
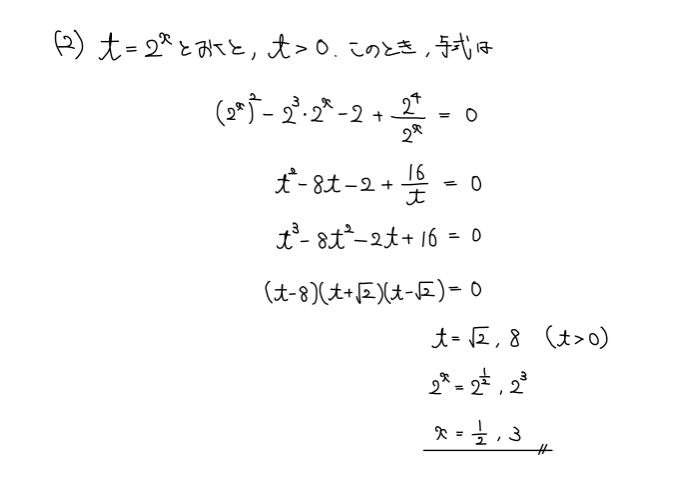
解説
典型的な指数方程式の問題。
ここは必ず点を取っておきたい。
t=2xと何か文字で置くときには必ず変域(値域)に注意する。
文字でおけばその後は整関数(3次)の方程式。
(3)整式の除法・定積分
解答

解説
一見大変そうに見えるが、基本通りに処理。
割る式と余り、2次式という条件から求めたい関数を式で表す。その際に条件は
[P(1)=a(x-1)2+b(x-1)+1 (a≠0)] or [P(1)=1 , P(x)=ax2+bx+c (a≠0)]
のどちらかで処理。a≠0という記述を忘れないように注意したい。
後は整関数で表せているからそのまま代入して積分。
P(t)とP(x)の両方に代入してxについての恒等式として見て計算しても良いが、右辺のP(x)はP(x)のまま計算する方が良いだろう。
さいごに
難易度としては、東京の私立で言えばGMARCHを受ける人はこれくらい解けていて、日東駒専を受ける人には難しく感じそう、という印象だ。
問題集通り典型問題のままというわけではないが、問題集でトレーニングを積んでいればすぐに処理は思い付くというレベルだ。
解けなかった人はしっかりとこれからもトレーニングを積んでいこう。
解けた人はしっかりとした方針決めができているため、もう少し偏差値の高い大学の過去問を解いてみても良いかもしれない。
数学としてはテンプレ問題なのかもしれないが、自分としてはしっかり解けて楽しい問題だった。



コメント