2020年度 中央大学の過去問を解いたので解答・解説記事をしていく。
今回解答・解説をしていくのは経済学部の一般入試を扱っているのには注意してもらいたい。(理工学部の入試ではない)
早速見ていこう。
問題(大問1)

まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
全体概評
中央大学は偏差値60.0〜62.5の私立大学(2021年6月1日時点 パスナビ調べ)。
難易度としては難問ではなく、典型的な問題と言える。
大問2はテーマ1つの小問2つで構成されている。
同一テーマの問題は誘導を意識して考えるようにしたい。
(1)xとyの関係式
解答
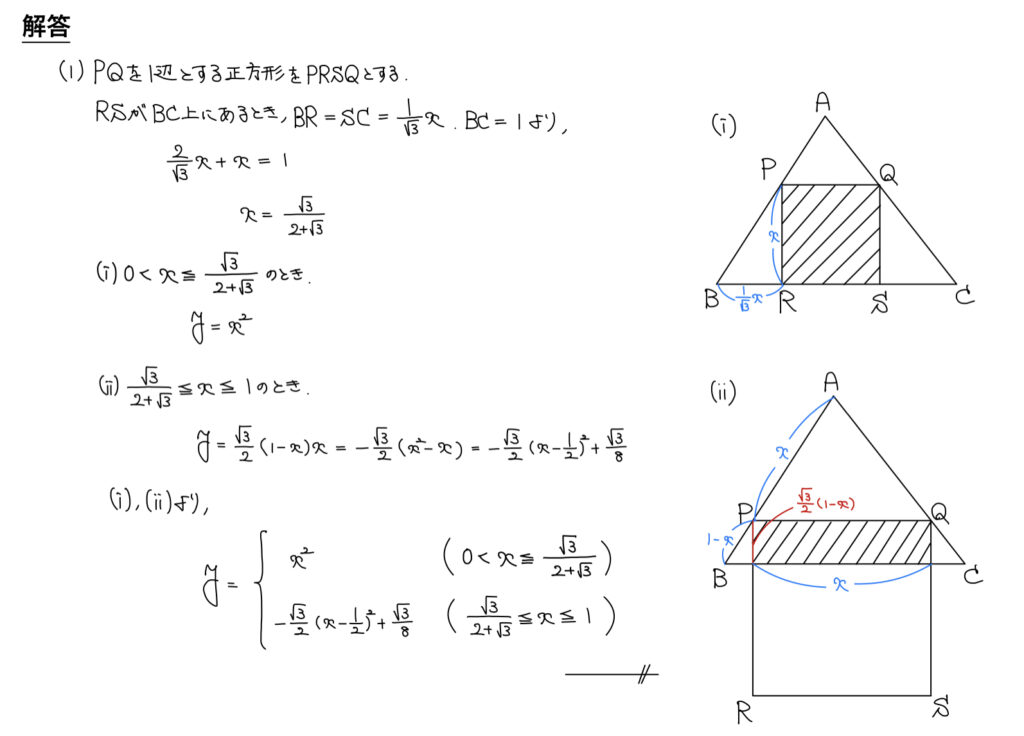
解説
正方形が三角形の内部に全て収まる(面積が単調増加)場合と正方形が三角形の外側まで出ていく場合で場合分けを考える。
(ⅰ)としては1辺がxの正方形の面積になるから面積自体は直ちに求めることができる。
問題はxの動く範囲がどこかだ。
(ⅰ)と(ⅱ)の境目はRSがBC上のとき。
となれば、その条件のxを考えれば良い。
パッと思い付くのが難しい問題は必ず図示して状況を整理しながら考える。
xの定義域さえ分かればそこからはそんなに難しくないだろう。
(2)面積の最大値
解答
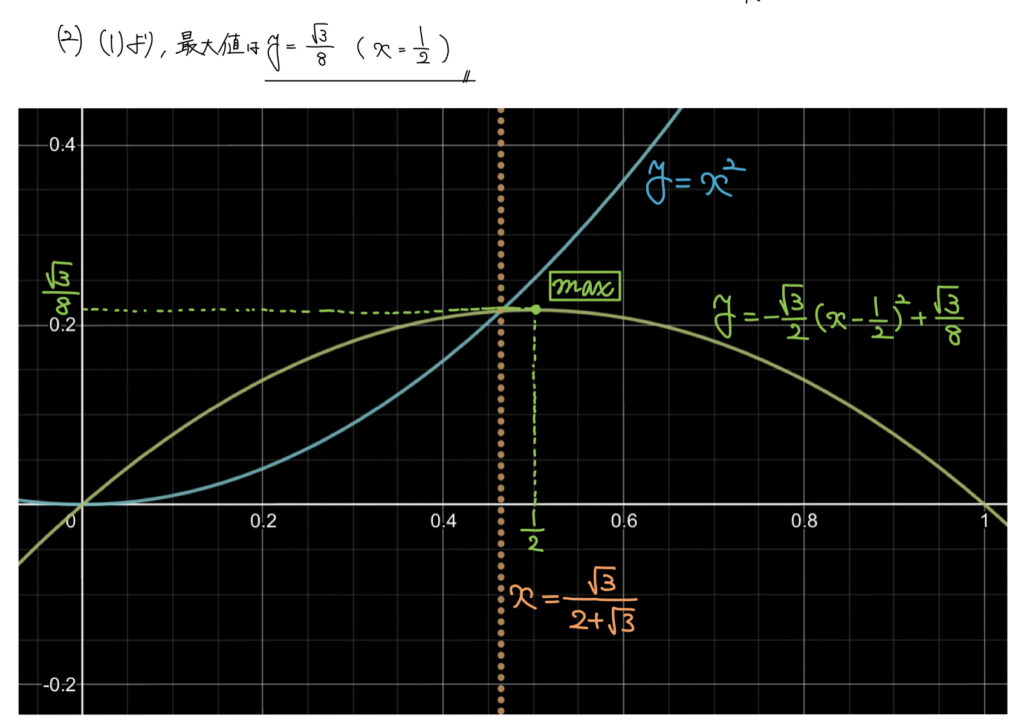
解説
面積の最大・最小問題は関数の最大・最小問題に帰着させる。
(1)で定義域の境目が求まったため、そこから引き続き考えていく。
境目以降も(ⅱ)の範囲は増加するため(ⅱ)の最大が面積の最大値。
2次関数の最大・最小問題は平方完成して得られる。
さいごに
難易度としては、教科書の章末・演習問題レベルという印象だ。
場合分けさえできていれば正答率はグッと上がりそうだ。
場合分けが思い付かなかった人は図示して状況整理しておきたい。
自分としてはこういった場合分けがある問題は好きだ。
高校入試の延長戦のような感覚を持って楽しみながら解けた。



コメント