東大の数学で合格点をとるまでの軌跡。
前回→『東大数学への道11』
初回→『東大数学への道1』
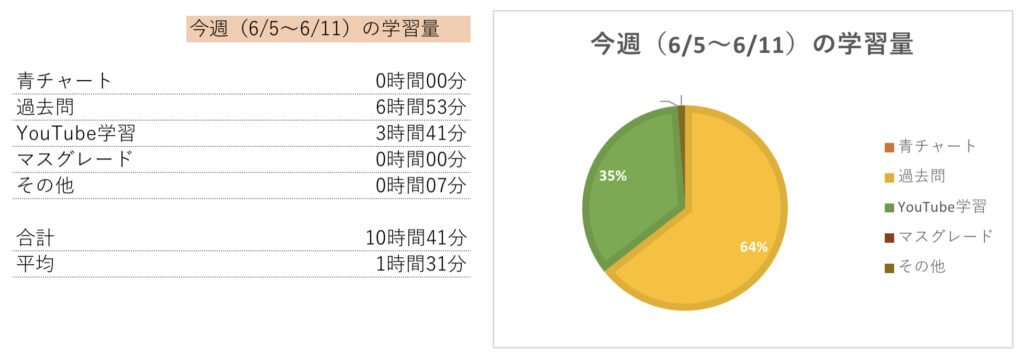
今週(6/5〜6/11)の学習量
合計は10時間41分であった。
1日平均は1時間31分だ。
今までの学習量推移も可視化しておこう。
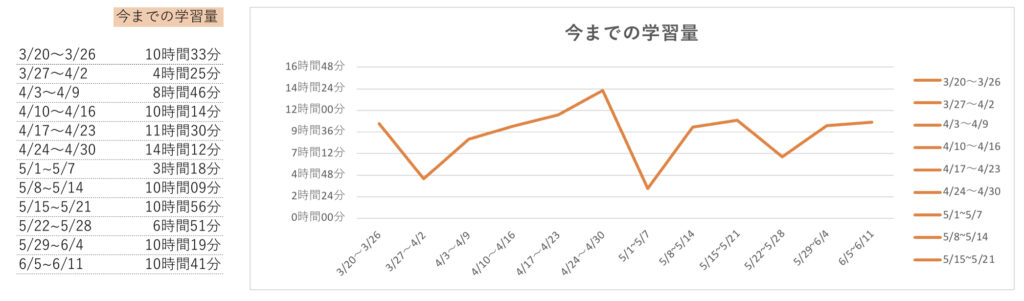
仕事で忙しくなる週に普段通りの勉強量を確保できたのは良かった。
とはいえTwitterで他の勉強している受験生や社会人の方々を見ると自分の勉強量の少なさに悔しさを感じる。
自分がやらなきゃいけないことは
- ありったけの時間を確保すること
- 少ない時間で最大の効果を出すためにどうするべきか思考しながら学習すること
だ。
自分は1日10時間勉強に時間を割くというのは物理的にどうしても難しい。
たまたま1日程度はそういうこともできるだろう。
それが出来る日なのにやれていない日があるのは反省だ。
その一方で、10時間を習慣とすることは出来ないこと、つまり、勉強量で周りに劣ることは自覚してそれを埋めるべく勉強しなければいけない。
幸いにも、自分は受験生の当時とは異なり、勉強法に関しての知識がある。
教育学や脳科学、心理学等の勉強に関する本を数多く読んできた過去の自分を褒めたい。
つまり、知識はある。ただ、改めて振り返ると実践で試せていない気もする。
- 自分が自分の勉強方法を見たらなんて思う?
- 自分にアドバイスするならどんなアドバイスをする?
結局主観的になると持っている知識の真価が発揮されない。
さらに、冷静に物事を見れない。
そういうところはもっと客観的で俯瞰的でなければならない。
そういう時に「自己解説・自問自答」というのは有効だ。
今は過去問にしがみついてそこにばかり注力をし過ぎている気がする。
目的は「数学力の向上」で「〇〇大学の過去問を解けること」ではない。
理解と知識は体系化・抽象化して、それを実践で扱う。
2つで1セットなのだ。
改めて過去の勉強法を振り返ると、実践ばかりに目がいき、体系化や抽象化が疎かになっている。
それじゃ同じ問題が解けるに留まってしまう。
それではだめだ。
どんな場面ならその定理が使えるのか、どうしてそう言えるのかというところをもっと深掘りしなければいけない。
体系化や抽象化ができている人は、一見全然違う問題でも(本質的にやること一緒じゃん)と思える。
自分はまだそこまでいけていない。
自分の成長には何が現実的にベスト勉強法なのか、根拠を含めて改めて考えていく必要がある。
自分は本質的な目的は受験ではないから周りと比較することに意味はないのだが、こうして改めて考え直させてもらえたのはTwitterの勉強アカウントの方々のおかげだ。
ありがたい。
「最も成長したのは自分だ。」
そう胸を張って言えるようにしよう。
どうせやるなら全力で。
過程確認
また今週も過去問を解いていた。
富山大学と東京電機大学だ。
満点こそとれなかったもののだからこそ学びはあった。
数学Ⅲの知識で抜けている部分は多そうだ。
解法暗記に頼ってしまっている部分があり、問題自体は解けているが体系化はされていない。
この問題は何故そのアプローチが有効なのか、類題でどんな形式のものがあったか。
他の形式の問題ではどういう出題が多くて、そういう際はどういう解法が有効なのか。
そういったことが言語化出来ていない。
もう一度青チャートをやりながら体系化をしていこう。
反省点と改善策
勉強時間
「今週の学習量」のところで述べたように、これからは勉強法をより工夫していく。
だが、工夫しようとも勉強量は絶対的に必要だ。
自分は天才ではない。
当然のことだが量も質も両方求めなければいけない。
まず、これからは朝1時間の勉強をしよう。
このルールの実現のために必要なのは前日夜の準備だ。
前日夜に
- 翌日何を勉強するかの整理
- 勉強道具の準備を机にして寝る
- 翌日の身支度・仕事準備を全て済ませる
- 睡眠時間の十分な確保
をしておく。
とりあえず来週1週間だけしっかりやり切ろう。
また、どこでも数学をやろう。
寝転んでいても、歩いていても、料理をしていても。
結局、想起と再言語化によって知識は定着し、理解は深まっていく。
考える時間さえあれば数学はどこでもできる。
しっかり考える材料を得るために、間違えた問題の写真をいくつか撮って、アルバムを作成、それらを思い出す(または写真見て考える)ようにしよう。
案外自分の間違った問題は悔しくて忘れられないものだ。
それを何度も反芻しよう。
どんな時間机に向かっていても、いつでもどこでも数学やっている人には敵わない。
それを体現していくことで時間をカバーしよう。
その分、机に向かえる貴重な時間はより濃い勉強へとしていこう。
勉強内容
まず、過去問についてはGMARCH程度を週に2,3校解いていく。
これは現在の知識で解ける問題もあるレベルで苦手な分野や単元、忘れている知識を炙り出すためだ。
東大の過去問をやろうかと思ったが、ただただ実力不足、分不相応だ。
過去問演習と並行して来週から本格的に進めるのが、徹底した青チャートでの単元理解・解法の言語化とマスグレードでの類題演習だ。
目指すのは問題を解く中で「この形はこれが有効だからこの処理」と言語化できることだ。
そして、実際に問題を目の前にしなくても「〇〇に関する問題はこういうパターンがあって、それぞれこういう処理をすればいい」と自分なりにまとめていけたら最高だ。
これからはより言語化を深く追求していく。
また、模範解答を必ず確認し、論理展開をしっかり追っていく。
「なぜこの1行が必要なのか」というところにも少し目を向けていきたい。
もし分からない論理展開を見つけた際には、教科書の確認をし、それでも不明であれば写真を撮って保存、いつか解決できるように準備しておくようにする。
来週の目標
さて、来週の目標を決めよう。
下記範囲は最低ラインとして設定した。
プラスαの部分は当日必要だと感じた部分を勉強する。
(最低ラインの設定ミスってる説はある)
13日(日)
確保時間:180分
朝:青チャート数学Ⅰ・A(60分)
入試問題解き直し(60分)
青チャート数学Ⅰ・A(60分)
14日(月)
確保時間:260分
朝:青チャート数学Ⅰ・A(60分)
YouTube学習(30分)
青チャート数学Ⅱ・B(60分)
2020年度入試過去問題「金沢大学」(120+50分)
15日(火)
確保時間:250分
朝:青チャート数学Ⅰ・A(60分)
YouTube学習(30分)
青チャート数学Ⅰ・A(60分)
青チャート数学Ⅱ・B(60分)
マスグレード(60分)
16日(水)
確保時間:250分
朝:青チャート数学Ⅰ・A(60分)
YouTube学習(30分)
青チャート数学Ⅰ・A(60分)
青チャート数学Ⅱ・B(60分)
入試問題解き直し(60分)
17日(木)
確保時間:360分
朝:青チャート数学Ⅰ・A(60分)
YouTube学習(30分)
青チャート数学Ⅰ・A(60分)
青チャート数学Ⅱ・B(60分)
2020年度入試過去問題「中央大学(理工)」(100+50分)
11日(金)
確保時間:330時間
朝:青チャート数学Ⅰ・A(60分)
YouTube学習(30分)
青チャート数学Ⅰ・A(60分)
青チャート数学Ⅱ・B(60分)
入試問題解き直し(60分)
マスグレード(60分)
12日(土)
確保時間:150分
朝:青チャート数学Ⅰ・A(60分)
YouTube学習(30分)
青チャート数学Ⅱ・B(60分)
今のままじゃ来週の予定を達成するのに不可能感あるが、実は結構出来そうな気がしている。
やってのお楽しみとしよう。
まとまらない文章になってしまったが、やる気は沢山書き込んだ。
あとはやるだけだ。
来週が楽しみだ。



コメント