2020年度 東京電機大学の過去問を解いたので解答・解説をしていく。
今回解答・解説をするにあたり、数学Ⅲを含む問題の前期入試を扱っているのには注意してもらいたい。(数学Ⅱ・Bまでの入試ではない)
早速見ていこう。
問題(大問2)

まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
東京電機大学は偏差値42.5〜55.0の私立大学(2021年6月13日時点 パスナビ調べ)。
大問2はテーマが1つとそれに付随する小問が4問。
辺の長さが等しいところも多く、対称性を意識したい。
問題の難易度は日東駒専レベルだろうか。
難問というものは特になく、教科書レベルの基本的な問題だ。
最後の計算が少しだけ不安になるかもしれないが、焦らず丁寧に計算すれば良い。
なお、小問一問一問の解法は基本的な解法になるため、しっかり知っておきたい。
(1)空間の位置ベクトル(ベクトルの分解)
解答
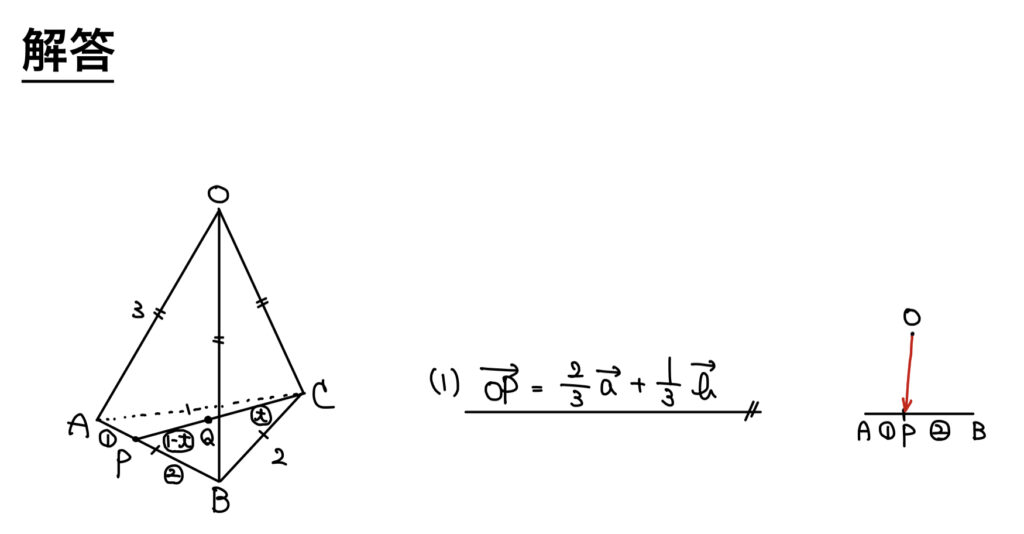
解説
タイトルを「空間の位置ベクトル」にしようか悩んだが、問題文から三角形OABに着目することは明らかなため、「平面の位置ベクトル」とした。
ベクトルの分解問題についての処理は以下の通りだ。
- 始点と基準となる(1次独立な)ベクトルを設定する
- 比を考える(チェバ・メネラウス・図形の性質の利用)
- 始点と終点を含む直線を抜き出して立式
- 始点からの直線上(実数倍) or 始点を含まない直線上(係数の和が1)
- 係数を文字でおく
また、空間においての解法も定石はあり、
- 始点と終点を含む平面を切り取って平面で考える
- 似た問題からヒントを得る
- 図形を展開する
これらが有効で、特に空間を切り取って平面で考えるのは定石中の定石だ。
今回も四面体OABCの中から△OABを切り取って平面の位置ベクトルを考える。
平面に切り取りさえすれば、あとは内分点の典型問題通りに計算をしていく。
(2)空間ベクトルの内積
解答

解説
空間においても方針は(1)と同じで、扱う平面を切り取るというところにある。
(1)同様、△OABを切り取るとあとは内積の典型問題に見えるはずだ。
また、ベクトル問題において内積の登場場面は以下の4パターンに限られる。
- 定義(大きさとなす角)
- 成分(同一成分の積の和)
- 大きさの2乗
- 正射影
「内積を扱う問題」」と分かった瞬間に以上のどのアプローチが有効かを考える。
今回は辺の大きさが与えられている(解答の図参照)ため、1の「定義」か3の「大きさの2乗」が有効。
実際、定義を用いて解答のように示せる。
定義で示す場合には、なす角が必要なため、まずはなす角を求めている。
本問の解説はここまでで、以下雑談程度に思ってもらいたい。
3の「大きさの2乗」でも求めることはできるが、それは内積の定義の証明と全く同じ手順を踏んでしまうため、最初から定義を用いて求めれば良い。
上記の意味がよく分からなかった人で知りたい!という人は、
- 大きさの2乗による解答を作成してみる
- 内積の導入(余弦定理による導入)を一度調べてみる
ということをすれば理解いただけると思う。
何を定義とするかは教科書・参考書・サイトなどによって様々だと思うので注意してほしい。
正直どれを定義としても他を示せるため、どれを定義とするかは重要ではなく、定義から他を示せるかというのが重要だ。
(3)空間の位置ベクトル(ベクトルの分解)
解答
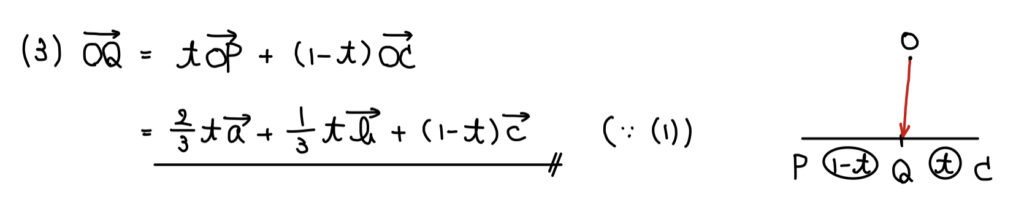
解説
(1)とやることは全く変わらない。
今回は始点Oと終点Qを含む平面の△OPCを切り取れば良い。(もっと言えば、解答のように始点Oと終点を含む直線PCだけで良い)
あとは内分点の典型問題通りに計算をしていく。OPベクトルは(1)を利用しよう。
(4)ベクトルの大きさの最大・最小
解答

解説
ベクトルの大きさの最大・最小は「2乗して考える」というのが定石だ。
なぜ大きさを2乗するかと言うと、2乗することで内積の話に持ち込むことができ、内積は分配法則など色々な性質を扱える、すなわち、やれる式変形の選択肢が増えるからだ。
解答では全体を2乗するわけではなく、平方根の中身だけを考えているがやっていることは同じだ。
自分は全体を2乗して、最後に平方根をとり忘れるという初歩的なミスが怖いためしないようにしている。
大きさの2乗を考えるとtの2次式という形になることが見え、そこでbとcやcとa(それぞれベクトル)の内積が必要だということがわかる。
内積は(2)と全く同じ手順で求められる。
tの2次式の最大・最小は平方完成で求めよう。
値が大きいため計算が少し怖いため、計算は慎重にやっていこう。
さいごに
問題を解いた印象としては、2020年に関しては日東駒専と同等かなという印象だ。
GMARCH志望の人は解けなければいけない難易度だ。
計算こそ少し手間だが、問題集通りの典型問題と言えるため解けなかった人は問題集でトレーニングを積んでいこう。
ベクトルは解法の手順が見やすい分野のため、今回の問題が解けること以外にも「この問題はこの手順で考えよう」というまとめを作っていくと良い。
空間ベクトルは自分も苦手なため、適切な平面を切り取りながら考えられるよう演習していきたい。



コメント