ベクトルの問題について扱う「ベクトル道場」シリーズ。
今回解いたのは「2020年度 福島大学(前期入試:人文社会学群) 大問4」だ。
難易度目安【易 ★★★☆☆ 難】
では見ていこう。
問題

まずは解説より先に問題を解いてもらいたい。
分からなかった人は解説を見てもらって、方針を参考にした上でどこから解けていないかを炙り出してもらえれば嬉しい。
では、問題解くの頑張って!
〜答案作成中〜
お疲れ様でした。
それでは、解答解説を始めていこう。
概評
難易度は東京の私立でいえば「GMARCH合格者で悩む人も一定数いる」というレベルだろうか。
日東駒専志望で解けていれば力がある方といえるのではないだろうか。
(2)はGMARCH合格者であれば正答率は相当高いだろう。
しかし、(1)をxの変域まで出して解けるというのを条件にすると正答率がグッと下がりそうだ。
ゆえに、この問題のポイントはxの変域までしっかり出すというところにあるだろう。
解法は基本通り行えばいいため、初見の形の問題でもいつも通りの方針で解いていこう。
それでは、一問一問楽しみながら見ていこう。
(1)平面ベクトルの内積
解答

解説
ベクトル問題で垂線やcosの値と言われれば内積に結びつくのは必然だろう。
それを常に念頭に置きながら考えていく。
まず、基準となる2つのベクトルを設定する。
平行四辺形OACBというところから始点をO、A方向とB方向に設定しよう。
あとはCやPの位置ベクトルも全部表していこう。
全ての点の位置ベクトルを表すことができたら、その後は内積からxとcosθの関係式を得る。
あとはcosθ=の形にすればいいわけだが、ここで重要なのが0で割ってはいけないというところから2x-1≠0を言わなければいけないことだ。
正直、2x-1≠0程度であれば直ちに求めることができるわけだが、そうではなく、xの範囲まで出せると尚良い。
気付けばで構わないと思うが、(2)でxの範囲を聞いているところから、ここで少し絞っても良いという発想からだ。
結果的に、(2)を解く上では2x-1の範囲について考えなければならない。
さて、ではどのように求めたら良いだろうか。
まず、2x-1≠0が知りたいわけだから2x-1=0を仮定して矛盾を示せばいい。
2x-1=0とするとPはBCの中点となるわけだが、これはあり得ない。
中点とすると三角形BOCが成立しない。それは図で見てもらえれば分かるだろう。
ここで2x-1≠0は示せるわけだが、図示をすると同時に2x-1<0にも気付くことになる。
つまり、今回は状況の整理のために図示をすれば良かったということだ。
図形の問題で状況把握が困難な際には、図示をしたり具体化してみたりしてみよう。
解法や条件が見えてくることがある。
こうして(1)の結論を得る。
(2)三角比、一次不等式
解答
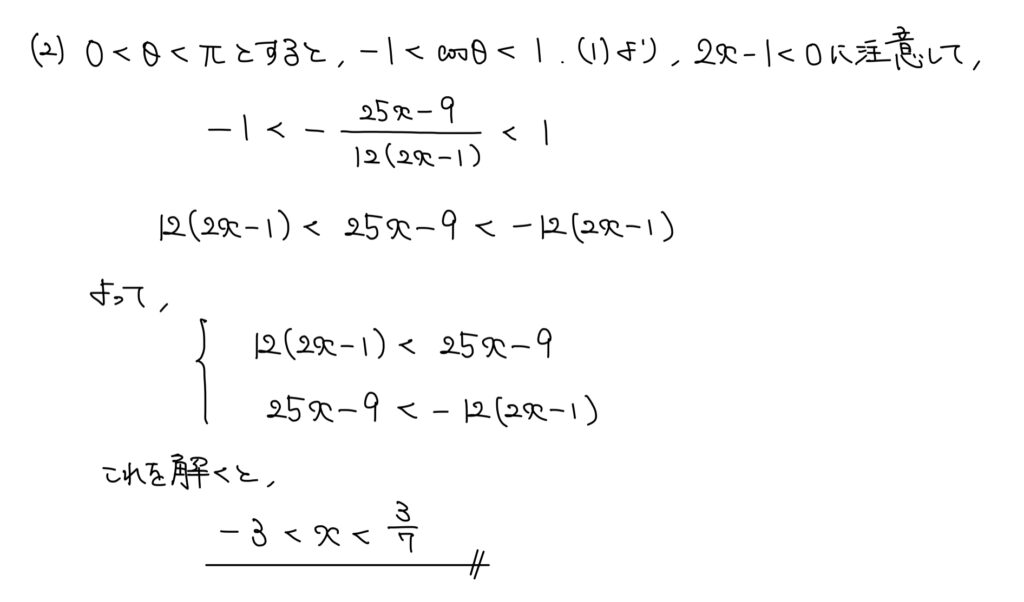
解説
(1)でxの範囲まで出してしまえば(2)は楽勝だ。
三角比の典型的な範囲問題。
θの範囲から三角比の範囲が決まり、関数の範囲が決まる。
これはよくある流れであるため知っておこう。
あとは2x-1<0に注意しながら丁寧に式変形をしていこう。
計算ミスは勿体無い。
さいごに
自分はこの問題を最初に見た時、(垂直ってことは内積問題か、得意分野だ!)と思い意気揚々と解き始めた。
そしてxの範囲でどうしようと思いとどまり、軽く図示したら解法が見えてきたという、作問者の手の平で踊りながらの思考をしていた。
こういうただ内積の計算をゴリゴリしていればいいだけではない問題はあまり出会わないため、とても楽しかった。
手の平で踊るのも悪くない。
しっかり踊れてよかった。
やるな…福島大学…!
何か解答不備などあったらコメントで教えてもらえればありがたいです。
一緒に頑張っていこう。
※無断転載や商業目的の利用は控えていただきますようお願いします。



コメント