2020年度弘前大学の過去問を解いたので解答・解説をしていく。
今回は理系全般共通の問題を解いた。(理工学部数物科学科の選択問題ではないので注意)
それでは、早速見ていこう。
問題(大問2)
目安時間:20分
2020年度 弘前大学 前期日程 理学部 数学
[ https://nyushi.hirosaki-u.ac.jp/wp-content/uploads/2020/05/R2ze-su2.pdf ]
※上記URL:国立大学法人弘前大学HP 『過去の入試問題』ページより 令和2年度 前期 数学②ⅢB
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。
参考URL『国立大学法人弘前大学HP-過去問題-』https://nyushi.hirosaki-u.ac.jp/faculty/previous-exams/
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
弘前大学は偏差値45.0〜52.5の国立大学(2021年8月1日時点 パスナビ調べ)。
大問2は関数についての問題だ。
難易度としては大問1同様標準的。
問題集に載ってそうな問題だ。
「接線のy切片」という設定だけ見慣れないが、方針決めは迷わないだろう。
関数も色々問題の出し方はあるが、接線の方程式と最大・最小はしっかり得点源にしたい問題だ。
対策しやすかったり、パターン化されていてやることが決まっているというのも得点源にしたい理由だが、1番の理由は周りの受験生の正答率が高いことだろう。
周りの受験生に差をつけられないためにもしっかり正答したい。
大問1に続いて計算問題だが、気を抜かず解いていこう。
(1)接線の方程式
解答
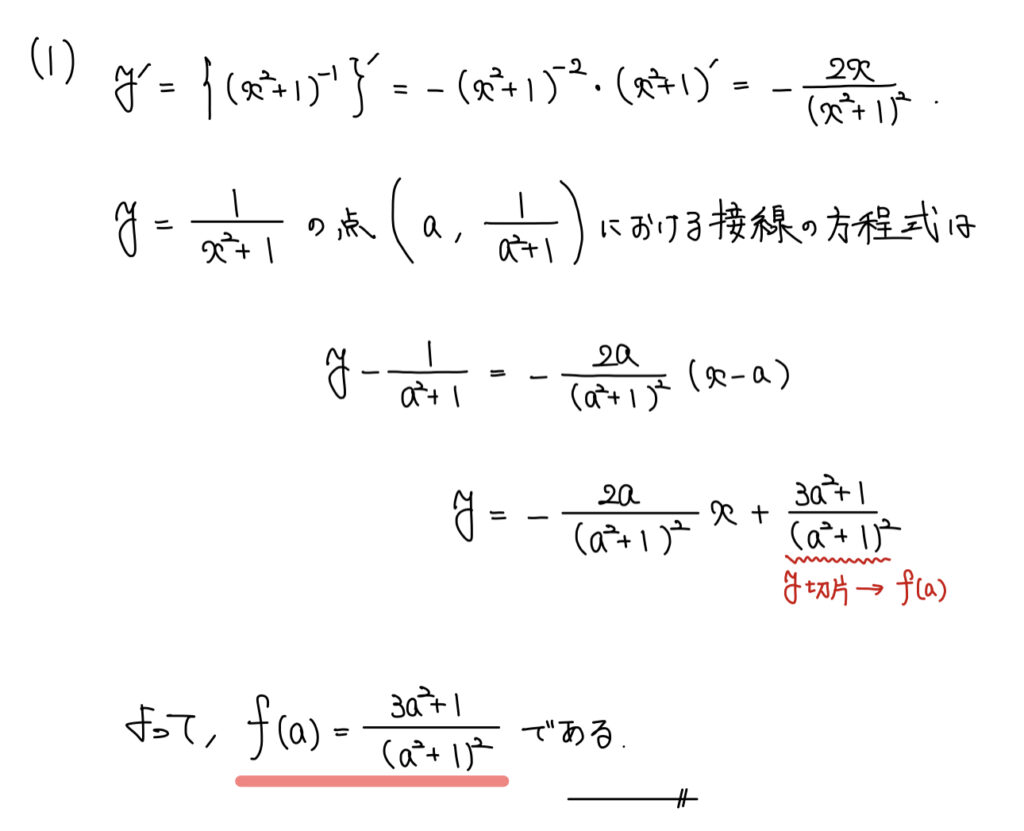
解説
「接線のy切片」をf(a)としているため、まずは接線の方程式を求めよう。
接点が与えられているため、微分して公式代入で終了だ。
あとは接線のy切片をf(a)として答えよう。
(2)分数関数の最大・最小
解答
解説
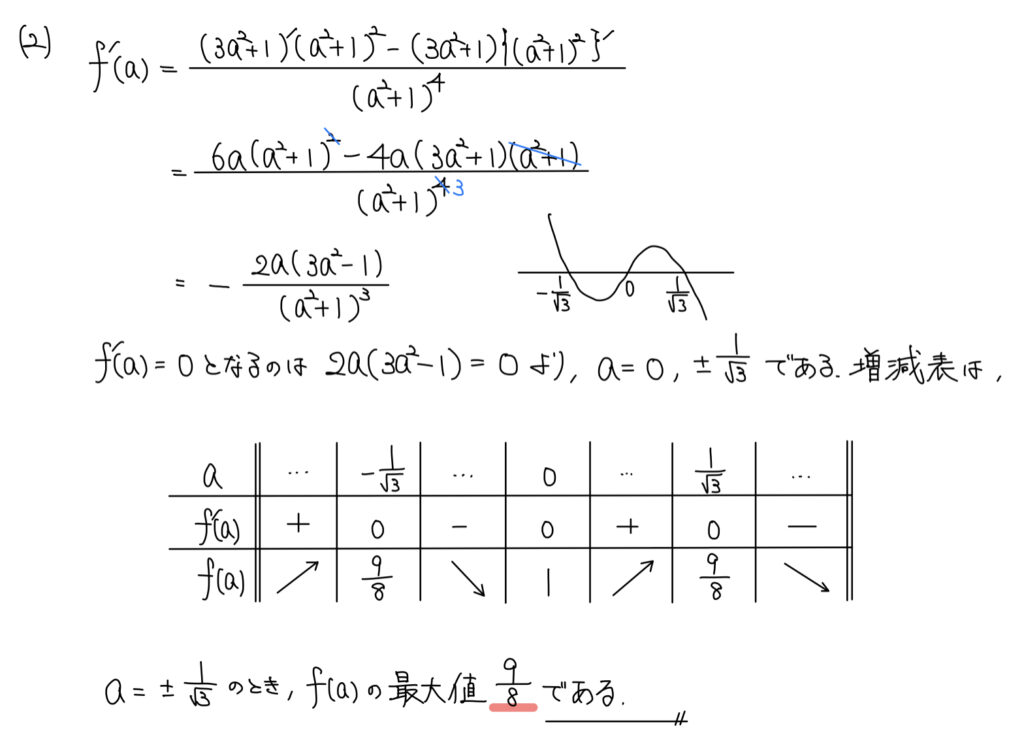
(1)でf(a)が分数式であるから、分数式の最大・最小問題だ。
やることは決まっていて、
- 微分して
- f’(a)=0となるaの値を求めて
- 増減表かいて
- (左右方極限を調べて)
- グラフイメージして
- 最大・最小を求める
という手順だ。
これは分数関数に限らず、様々な関数においても同様だ。(定関数、1次関数、2次関数を除く)
計算ミスをしないように気を付けよう。
さいごに
公式の模範解答はこちら
https://nyushi.hirosaki-u.ac.jp/wp-content/uploads/2020/05/R2ze-su2_kaitou.pdf
参考URL:国立大学法人弘前大学HP 『過去の入試問題』ページより令和2年度 前期 数学②ⅢB 解答例
大問1に続き基本的な問題と言える。
高得点が予想される(特に医学部医学科)ため、取りこぼさず完答を目指そう。
正答でも大きく差がつくほどでもなさそうだが、完答であれば他教科のフォローもできるだろう。
計算ミスにだけ要注意して解いていこう。
個人的には思考することもなく、ひたすらペンを動かす問題で好みの問題ではなかった。
もう少し思考力や発想力を問われる問題をやりたいな。
とはいえ、しっかりミスせず解けたことは誇りに思おう。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント