2021年度静岡大学の過去問を解いたので解答・解説をしていく。
今回は前期日程・理学部数学科の問題を解いた。
学部学科によって問題が異なるため、特定の学部をピンポイントで解きたい志望者は注意して欲しい。
それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『静岡大学 過去問』で検索してみて欲しい。
目安時間:20分
2021年度 静岡大学 前期日程 数学
[ https://www.shizuoka.ac.jp/nyushi/information/pdf_2/r03zenki/m3.pdf ]
※上記URL:国立大学法人静岡大学HP > 学部入試 > 過去問題 > 過去問題令和3年度 > 理学部数学科 > 数学
※過去3年分が公式HP(下記URL)から閲覧できます。(2021年8月15日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人静岡大学HP-学部入試-』
https://www.shizuoka.ac.jp/nyushi/information/index.html#a04
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
静岡大学は偏差値47.5〜55.0の国立大学(2021年8月15日時点 パスナビ調べ)。
大問2は数列・級数の問題だ。
難易度としてはGMARCHレベルだろうか。
(1)は全員正解しているくらいの問題で、(2)も正答率は高そうだ。
(3)はそんなに正答率は高くないであろうため、差がつくとしたら(3)だ。
数列で見たことない問題は誘導に乗ることを意識して解いていこう。
本当は大問4つで120分のため、大問1つで30分使えるのだが、これで30分はかけすぎだ。
この大問であれば20分程度で解けるようにしておきたい。
それでは解答を見ていこう。
(1)数学的帰納法
解答


解説
すべての自然数についての証明では数学的帰納法が有効だ。
これは全員が知っている公式で、おそらく1度は解いたことがあろう問題であるため、確実に正解しておきたい。
(2)
解答
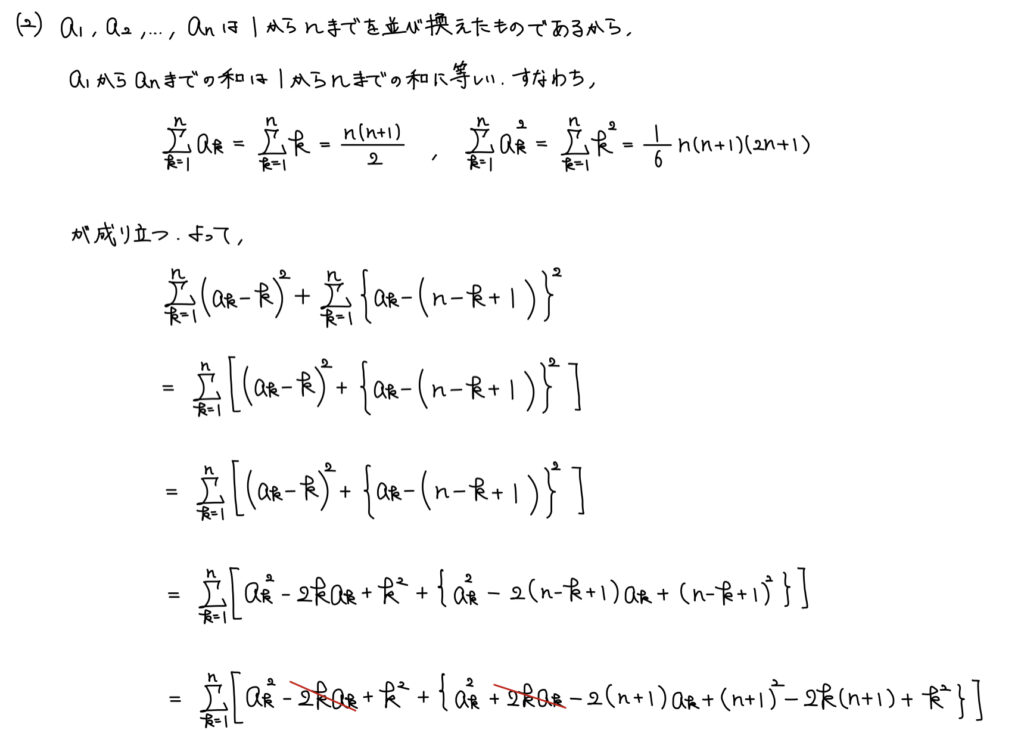
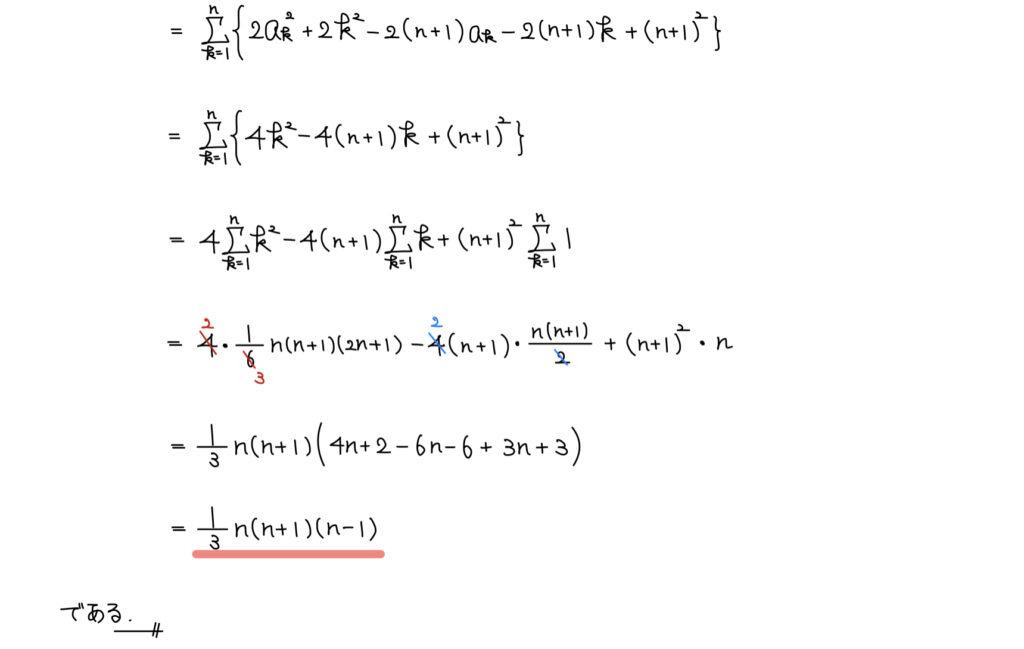
解説
今回の問題は式変形ではなく、解答の冒頭4行だ。
まず、数列を考える当たって重要なのは「その数列にどんな規則性があるのか」だ。
その関係は「等差、等比、階差」など様々だが、結局何かしらの規則性がないと基本的に数列問題は解けない。
逆に言えば、受験数学で出される数列は必ず解けるわけだから、必ず何かしらの規則性の上にある。
今回のような数式で表せないような規則性では、いつも扱う数列と同じところ、または違うところはどこだろうと考えるといい。
基本的に
- 一般項
- 漸化式
- 級数
- 推測可能か
くらいに着目したら良いのではないだろうか。
今回何番目に何の数字がくるか予想ができないため、一般項や漸化式は作れない。
しかし、どの数字があるかさえ分かれば順番は関係ないのが級数だ。
よって、今回は数列の級数にどんな規則性があるかを考えれば冒頭の3行が書ける。
そこからは単純に計算をしていけばいい。
(3)数列の最大・最小
解答
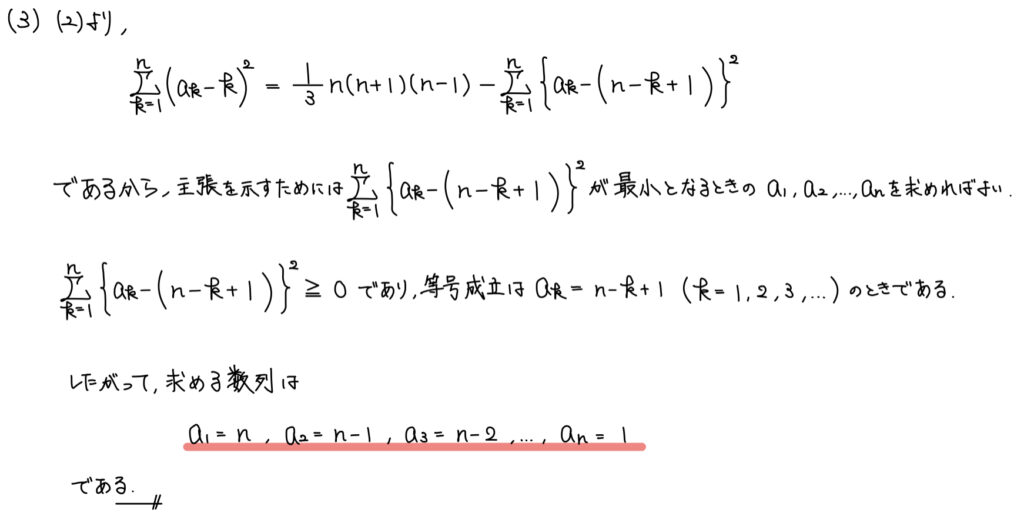
解説
(3)であるため、(1),(2)が誘導になっていそうと考えるのは自然な流れだ。
級数の最大(最小)は「マイナス(プラス)の値を足さないこと」を考えれば良い。
今回も足していく値の正負を考えていくのだが、2乗した値を足していくためakの値によらず必ず0以上になる。
このことから、最大値を考えるのは難しく、最小値は考えやすいことがわかる。
これは「思考の流れから当然この考えに至る」というものではなく、「(2)の流れを汲んで考えるとそうなる」というのが大きいように思う。
あとは0以上の値を足していくわけだから、最小なのは全て0のときだ。
こうして結論を得る。
さいごに
数列はこのように規則性がないものもあって、個人的にはこういう問題が面白い。
または、よく分からない数列を式変形したりして知っている形に持っていける問題が個人的には好きだ。
数列は順番が明確に決まっているため、規則性との相性が非常に扱いやすい単元だ。
これからは「数列の最大・最小問題は最大と最小を入れ替えることで解けることもある」というのを頭の片隅に入れて解いていきたい。
解いた方お疲れ様でした。
これからも一緒に頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント