2020年度秋田大学の過去問を解いたので解答・解説をしていく。
今回は前期日程の問題を解いた。
大問自体は全学部9題ある用紙を配布されるが、そのうちどの大問を選択して解答するかは学部学科によって異なるため注意して欲しい。
学部ごとにどの大問を選択すれば良いかは以下画像の赤枠内参照。

それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『秋田大学 過去問』で検索してみて欲しい。
目安時間:20分
2020年度 秋田大学 前期日程 数学
[ https://www.akita-u.ac.jp/honbu/exam/pdf/r2_zenki/r2zenki_05.pdf ]
※上記URL:国立大学法人秋田大学HPホーム > 入試情報 > 過去問題 > 令和2年度 > 前期日程 > 数学
※過去8年分が公式HP(下記URL)から閲覧できます。(2021年8月18日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人秋田大学HP>入試情報>過去問題』
https://www.akita-u.ac.jp/honbu/exam/ex_pastissues.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
秋田大学は偏差値42.5〜62.5の国立大学(2021年8月18日時点 パスナビ調べ)。
大問は3の2つの円についての問題だ。
難易度としては日東駒専以上GMARCH以下レベルだろうか。
(1),(2)は標準的な問題集にそのまま載っているような問題、(3)は今まで見たことがない問題かもしれないが基本事項を組み合わせれば解け、かつその方針も見えやすい問題で難問ではない。
目安時間20分というのもそんなに厳しい時間設定でもないのではないだろうか。
とはいえ、誰しもが正解できるという問題でもないように思う。
(1),(2)の基本事項をしっかり押さえながら、(3)の方針決めに着目して解答解説を見てもらいたい。
それでは解答を見ていこう。
(1)円の方程式、2つの円の位置関係
解答

解説
2つの円が外接する問題。
2円が「交点を持たない、内接する、外接する、2交点を持つ」というのを公式で覚えている人はそれを適用すれば直ちに求められる。(以降の解説も読み飛ばすことをオススメします)
自分は別に覚えてなくて、イメージしてその場で作っているため、覚えていない人もイメージだけすればいい。
自分が2円の位置関係で覚えていることといえば「2つの半径と中心間の距離で式を作る」ということくらいだ。
イメージの際には図を描くと良い。
イメージの図に関しては座標、半径の長さなどの正確性は必要なく、ただ状況(内接や外接)さえ合っていればそれでいい。
今回は「外接」のため外接の位置関係にある円を2つかけば、「2円の半径の和が中心間の距離に等しい」ことが見えるはずだ。
図形に関する問題は、図形を描いて具体化してあげることで条件が見えてくることがあるので、なるべくイメージは頭の中だけでなく図としてかきたい。
(図形問題の中でもベクトルは式処理がしやすいため図が不要であることも多い)
条件が見えた後は立式して計算して終了だ。
(2)円の方程式、2つの円の位置関係
解答

解説
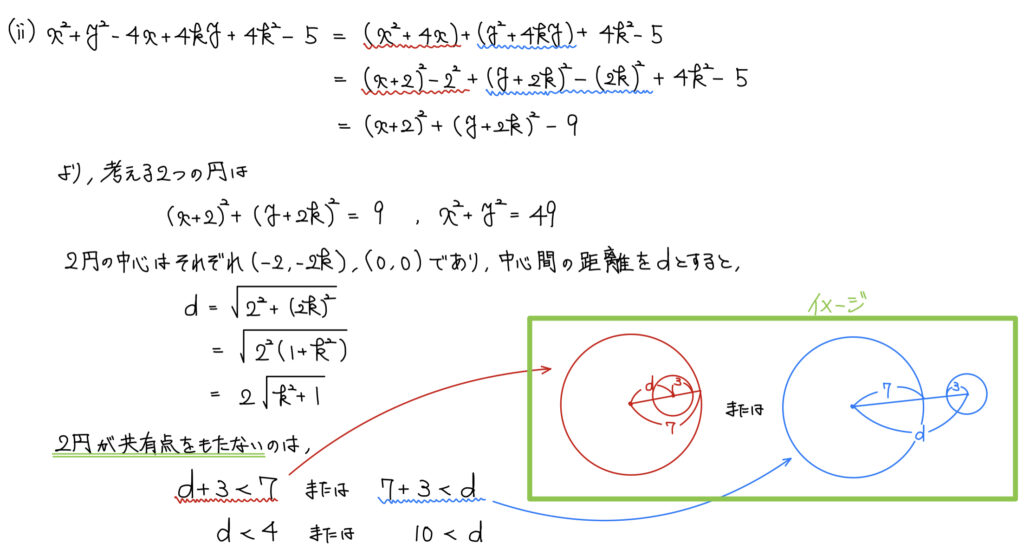
「2円が共有点を持たない」という条件が「式ではどのように表せるか」と問われているこの問題。
(1)同様、公式を知っている人は代入して終了。(以降の解説も読み飛ばすことをオススメします)
知らない人は図を描いてイメージすればいい。
交点を持たないのは「近すぎて内部」か「遠過ぎて外部」の2つのパターンがある。
それぞれを式にするため言語化すると「内接より内側」と「外接より外側」となり、更に言えば「中心間の距離と小さい円の半径を足しても大きな半径未満」と「中心間の距離が2円の半径の和より大きい」ということになる。
言語化してはみたが、正直イメージとなる図(解答の緑枠内部)を見てもらった方が遥かに分かりやすいだろう。
条件を立式出来たらそれぞれ解いてあげれば解答を得る。
(3)円の方程式、交点の座標
解答


解説
【用語の説明】優弧…長い方の弧、劣弧…短い方の弧
この問題を解くポイントとなる流れは
- Pの位置をどうやって定めるか
- 円と直線の交点の座標をどう求めるか
- 優弧の点であることをどう表現するか
だ。
そもそも方針が全く立たなかったという人もいるだろう。
そういう人は
- 図を描いてイメージしていない
- 条件の言い換えができていない
- 基本問題への変換をしていない
というのがあるのではないだろうか。
図を描いてない人は図を描こう。
条件の言い換えは難しいが、「三角形の面積最大」→「底辺と高さが最大」のように問題文のままではなく、もっと何を求めればいいか分かるように言い換えていくことを意識していこう。
基本問題の変換は問題を全体で眺めず、求めたいものごとに分けて考えていくことが重要だ。
自分はこれを単に簡単なものに分割すると言っている。
最初に答えまでの方針を立てる(もしくは、条件を整理し終えて今やれることが何か見える)ことができたら、そこからは求めたいものごとに分割して、その単元ごとに求めていくのがいい。
例えば、面積が最大となるPの位置が分かったのに方針が立たなかったという人は、問題文全文に気がいき過ぎて「交点の座標は連立方程式で導く」という基本的な方針を見失ってしまったのではないだろうか。
これらが大まかな方針決めの仕方だ。
さて、長くなったが、この後は本題。
まず、問われているのは「三角形の面積が最大となるとき」のため、その状況を考える必要がある。
そこで、まず図を描いてイメージしてみよう。
図を描くと、Pが動いてしまうために求めたい三角形の概形が直ちには分からないことが確認できる。
この後「だから分からない」ではなくて、本当に面積が最大となるPの位置が分からないのかは確認したい。
今回A,Bが定点のため、ABを底辺とするとPは「高さが最大となるような円周上の点」ということになり、Pの位置が定まる。
かといって、「ここがP!」とすることはできず、あくまでPは「面積が最大のときの」点であるから定点はCとして求めておいて「面積が最大の時はCとPが一致」くらいが良いのではないだろうか。
(面積が最大となるときのみ考えることを先に言えばPが固定されるため、Cを準備しなくても構わない)
Pの位置が分かったら、次はその座標をどうやって求めるかを考えていく。
「座標を求める」と言えば、連立式かベクトルの成分が王道の解法だろう。
今回どちらで解くこともできるが個人的には連立式の方が簡単で、読者の方に馴染みやすいと判断したためそちらで解答を作成した。
では、連立式を作る場合、Cは何と何の交点なのだろうか。
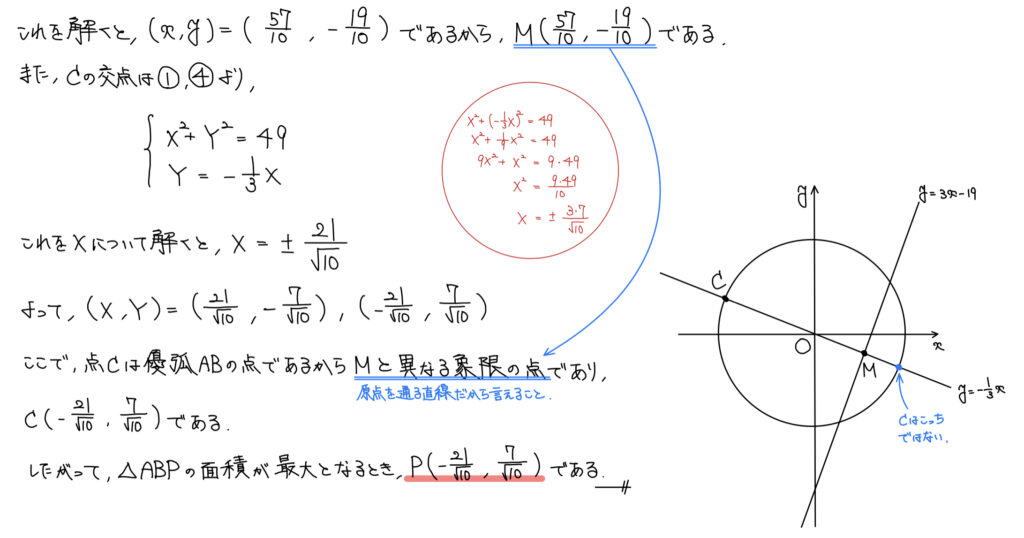
結論、Cは直線OMと円x2+y2=49の交点だ。
すると、円の方程式はx2+y2=49で既に分かっているため、話はOMの方程式を求めれば良いということになる。
直線の方程式は「通る2点」か「通る1点と傾き」が分かればいい。
原点を通ることは分かっているので、傾きかもう一点分かればいい。
これは「ABとの垂直」もしくは「ABの中点Mの座標」を求めることで解決だ。
よって、
- 直線OMの方程式分かる
- 円x2+y2=49と直線OMが連立できる
- 点Cの座標が求められる
ということまで分かる。
ここまで来たら最後。
連立式解いたら交点が2つ出てきたはずだ。
最後、2点のうちどちらが優弧側かを把握し、主張しなければいけない。
一般的に、優弧側を点C、劣弧側を点Dとすると、CM>DMが成り立つ。
これは数学の定理・公式の暗記というより図形的に考えた方が分かりやすい。
2交点のうち、弦の中点Mが近い方が劣弧、遠い方が優弧だ。
そこから説明してもいいが、今回は原点が中心となる円について話しているため、どの象限に位置するかの方が計算がなくて楽だ。
ゆえに解答はそちらを採用したが、もし(自分は原点に気付けないし、原点じゃない問題だったらどう解くの?)という人はCM>DMから優弧と劣弧のどちら側の点か把握すれば良い。
さいごに
今回は解答の方針を見失ってしまう人用に解答解説を書いたため、かなり長くなってしまった。
自分が書いている解答や解説は偏差値50〜55程度の人を目安だ。
数学が得意な人や解けた人にはかなり冗長に見え、当たり前に感じる事実も多くあるだろう。
その辺りは各個人勝手に読み飛ばしてもらいたい。
ブログの利点として、書籍と違って文字制限がないという部分があるため、自分としては綺麗な解答より分かりやすい解答を目指している。
そのためには無駄な途中式も書くし、実際は不要でも手助けとなる一文を添えたりしている。
自分のブログで考え方や方針決めを身につけてもらって、他の参考書などで綺麗な解答の書き方を身につけるのが良いと思う。
問題解いた方、お疲れ様でした。
これからも一緒に頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント