2021年度一橋大学の過去問を解いたので解答・解説をしていく。
今回は前期日程の問題を解いた。
それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『一橋大学 過去問』で検索してみて欲しい。
目安時間:21分
2021年度 一橋大学 前期日程 数学
[ https://juken.hit-u.ac.jp/admission/info/files/R3_suugaku_zenki_mondai.pdf ]
※上記URL:国立大学法人一橋大学HPホーム > 学部入試情報 >入学試験の「問題」及び「出題の意図等」 > 令和3年度入試 > 数学(前期日程) > 試験問題
※過去3年分が公式HP(下記URL)から閲覧できます。(2021年9月5日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人一橋大学HPホーム>学部入試情報>入学試験の「問題」及び「出題の意図等」』
https://juken.hit-u.ac.jp/admission/info/ito.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
一橋大学は偏差値67.5〜72.5の国立大学(2021年9月5日時点 パスナビ調べ)。
大問3は2次方程式、三角形の成立条件、関数の領域についての問題だ。
難易度はGMARCH以上早慶上理以下レベルの問題。
そんなに複雑な解法までの手順はなく、解答自体はすぐに作成できそうだ。
今回の解答では③として解いたが、実は条件の同値性を利用すれば③は調べなくても求められる。
しかし、そうしなくても解けるため、今回は一つ一つ条件を調べていく方針をとった。
確実と言えるが、綺麗な解答とは言えないし、ただただ無駄であると言えばその通りだ。
もっとスッキリした解答が気になる人はパスナビの模範解答を見ることをオススメしたい。
それでは解答を見ていこう。
(1)2次方程式、三角形の成立条件、関数の領域
解答


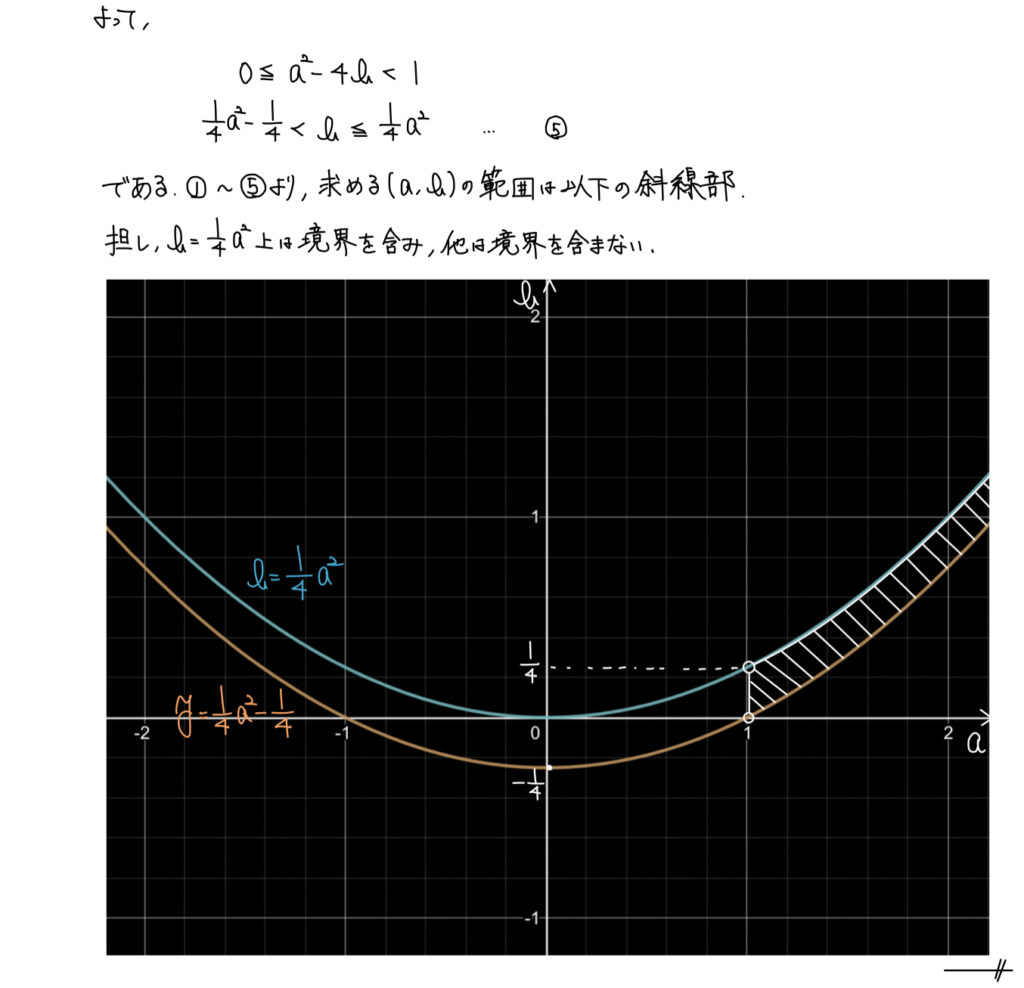
解説
解と係数の関係の利用は直ちに分かるだろう。
解の個数から判別式に注意しよう。
また、三角形の成立条件も分かりやすく見える形だ。
そして使う条件はこれらのみ。
あとは解の条件か範囲を絞りつつ、α,βの式ををa,bの式に変換していけばいい。
計算ミスにだけ注意してここは点数が取りたいところ。
(2)多変数関数の最大・最小
解答

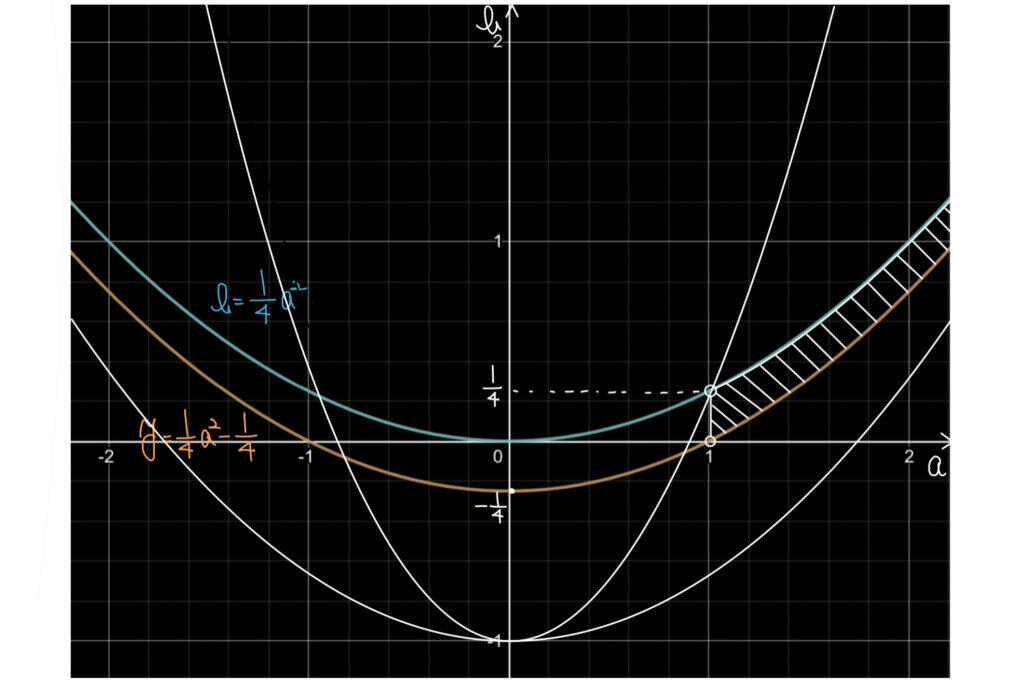
解説
多変数関数の最大・最小の解法は以下の通り。

今回は等式条件なし、予選決勝法困難なため「逆像法」での解法が有効だ。
ちなみに、等式条件というのは今回で言えば「α=2」や「α+β=3」のようなものがあれば①の解法だった。
逆像法は「=k」とおいてkの存在範囲を求めるというものだ。
(1)を利用するためにb=(aとkの式)の形にするのが良いだろう。
そのモチベーションで式変形ができればあとは(1)の図を利用しながら考えていくのが良いだろう。
さいごに
様々な単元の複合でありながら、その知識をちゃんと理解しているかをたった一問のこの短い問題で聞いているのだから流石の問題だ。
とはいえ、難易度としてはそこまで高くない。
逆像法をどういう場面で使うかを理解していなかった自分であれば難しく感じてたかもしれないが、正直一橋大学を受験する学生であればここはある程度解いていなければいけない問題と言える。
解けなかった人はどの単元のどの分野のどの基礎知識とどの発想は足りなかったのか言語化できるようにしておきたい。
解いた方お疲れ様でした。
これからも一緒に頑張っていきましょう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント