2021年度一橋大学の過去問を解いたので解答・解説をしていく。
今回は前期日程の問題を解いた。
それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『一橋大学 過去問』で検索してみて欲しい。
目安時間:21分
2021年度 一橋大学 前期日程 数学
[ https://juken.hit-u.ac.jp/admission/info/files/R3_suugaku_zenki_mondai.pdf ]
※上記URL:国立大学法人一橋大学HPホーム > 学部入試情報 >入学試験の「問題」及び「出題の意図等」 > 令和3年度入試 > 数学(前期日程) > 試験問題
※過去3年分が公式HP(下記URL)から閲覧できます。(2021年9月5日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人一橋大学HPホーム>学部入試情報>入学試験の「問題」及び「出題の意図等」』
https://juken.hit-u.ac.jp/admission/info/ito.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
一橋大学は偏差値67.5〜72.5の国立大学(2021年9月5日時点 パスナビ調べ)。
大問4は円と直線、定積分についての問題だ。
難易度はGMARCH以上早慶上理以下レベルの問題。
(1)は合格者のほとんどが正答であろう。
(2)についても図は比較的すぐに描くことができるため、求める面積は見えやすい。
あとは面積と重解を上手く利用する、もしくは典型処理で接線の方程式を求めてゴリゴリの計算から導いていくという方法でも求められる。
どちらにせよ複雑な解法の発想は必要なく、正答率が高いように思えるため、一橋大学志望の受験生は解いておきたい問題だ。
この大問も他の大問同様、複数の単元が混在するため方針が見えにくくなることがあるが、今自分はどんな問題に対峙していて、その時の基本処理はどんなだったかということをしっかり考えて紐解いていけば分かってくる。
それでは解答を見ていこう。
(1)共有点の個数(方程式の逆算問題)
解答

解説
自分は
- 方程式から解を導く
- 関数から交点を求める
といった問題、つまり、「方程式→解」の流れの問題を方程式を解く問題、逆に
- 方程式の解が与えられた状況で元の関数を決定する
- 交点の値や個数、範囲から元の関数を決定する
といった問題、つまり、「解→方程式」の流れの問題を方程式の逆算問題と読んでいる。
方程式の逆算問題は
- 式処理
- グラフ処理
の2通りの方針があり、それぞれ以下の通りだ。
今回の実際の解法の流れは
交点→連立式→解が1つ確定→残り2つもつ→2次関数より判別式
流れを把握して方針が決まればあとは計算をやるだけだ。
(2)関数の最大・最小、定積分
解答
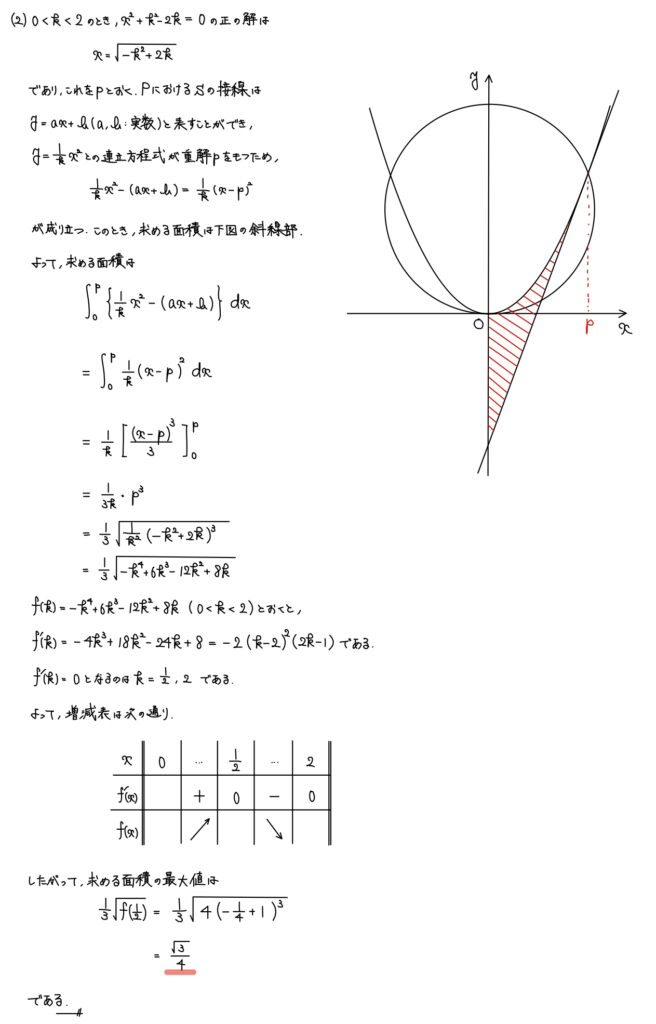
解説
求めたい面積を図示することは容易だが、交点をそのまま計算していくのはかなり煩雑だ。
そのため、解答では交点をpとおいて計算が多少楽になるように工夫した。
別にpとおかなくても解けるため、本問題の本質はそこではないが、重解の工夫の一つとして知っておいて損はないだろう。
あとは面積を求めるために定積分。
そして求めた面積の最大・最小ということで面積を関数として微分→増減表→グラフという流れ。
重解、定積分、関数の最大・最小と複合問題となっていることが、やっていること自体はかなり基本的な処理だ。
今自分が何を求めていて、次は何をすればいいのかというのを切り替えながら問題に臨もう。
さいごに
この問題は基本的でもありながら頭がこんがらがりそうな問題でもある良問だ。
受験者を篩にかけるという目的としてはとても良い問題ではないだろうか。
ちなみに、一橋大学の志望者としてはこれくらい解けておきたいというレベルでもある。
解けなかった人もここで問題に出会えただけで良かったのではないだろうか。
これから成長していけばいい。
解いた方お疲れ様でした。
これからも一緒に頑張っていきましょう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント