2020年度 小樽商科大学の過去問を解いたので解答・解説記事をしていく。
早速見ていこう。
問題(大問2)
※現在問題は非公開とさせていただいております。
過去問題は大学公式の問い合わせホームから直ちに請求できます。
費用もかかりませんので是非行ってみてください。
年度により請求できないものもあります。
公式サイト『国立大学 小樽商科大学 受験生サイト-過去問題請求ホーム』
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
全体概評
小樽商科大学は偏差値50の国立大学(偏差値はパスナビ調べ)。
難易度としては難問ではなく、典型的な問題と処理で解ける。
大問2は小問3つで構成されている。
この問題は多くの受験者が解けるであろうため、落とさないようにしたい。
(1)変数 t への変換、三角関数の合成
解答
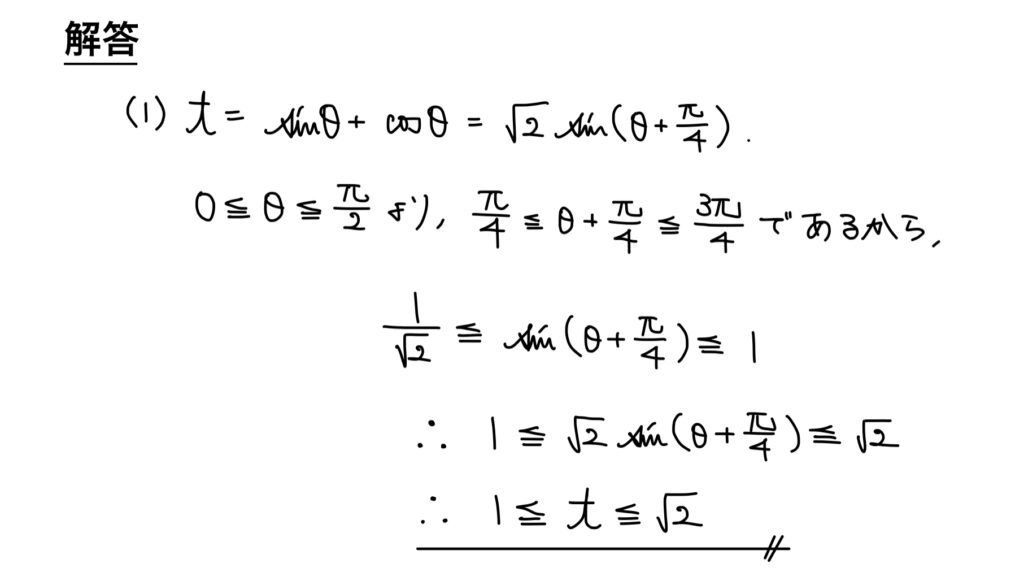
解説
sin2θ=2sinθcosθより、yはsinθ,cosθについての2次式。
三角関数の2次式はt=sinθ+cosθ …①とおくことをまず考える。
文字でおいたら変域注意。
tについての変域は①を合成することで得る。(これが定義域となる)
ここまでは典型的な処理のためしっかりできるようにしておきたい。
(2)三角関数から整関数への変換
解答
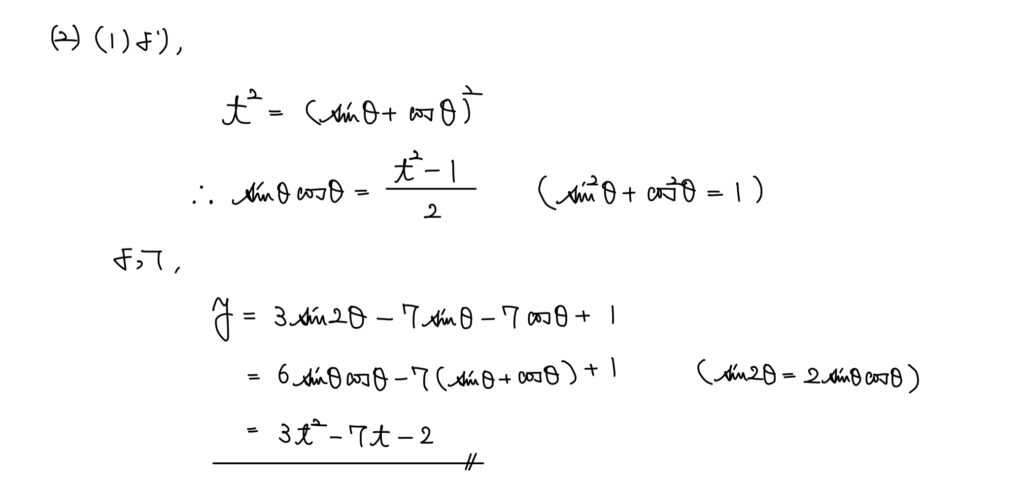
解説
(1)で変数を t へ変換したため、当然yをtで表したいという流れ。
三角比の相互関係や加法定理(倍角の公式)を用いながらyをtで表せるように変形していく。
sinθcosθの積の形が欲しい時は t を2乗して得る。
(3)三角関数の最大・最小
解答

解説
(3)の題として「三角関数の最大・最小」と表したが、(2)までで整関数へと変形してあるわけだから実質整関数の最大・最小問題とも言える。
整関数の最大・最小処理は次の通り。
- 1次式 → 傾きの正負(単調増減の確認)と定義域で処理
- 2次式 → 平方完成と定義域で処理
- 3次式以上 → 微分して増減表で処理
今回は2次式のため平方完成で解く。
さいごに
難易度としては、東京の私立で言えばGMARCHを受ける人はこれくらい解けていて、日東駒専を受ける人には難しく感じそう、という印象だ。
問題集通り典型問題のままというわけではないが、問題集でトレーニングを積んでいればすぐに処理は思い付くというレベルだ。
解けなかった人はしっかりとこれからもトレーニングを積んでいこう。
解けた人はしっかりとした方針決めができているため、もう少し偏差値の高い大学の過去問を解いてみても良いかもしれない。
数学としてはテンプレ問題なのかもしれないが、自分としてはしっかり解けて楽しい問題だった。



コメント