2020年度 中央大学の過去問を解いたので解答・解説記事をしていく。
今回解答・解説をしていくのは経済学部の一般入試を扱っているのには注意してもらいたい。(理工学部の入試ではない)
早速見ていこう。
問題(大問1)

まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
全体概評
中央大学は偏差値60.0〜62.5の私立大学(2021年6月1日時点 パスナビ調べ)。
大問1は小問6つで構成されている。
難易度としては難問ではなく、典型的な問題で教科書レベルと言える。
合格のためにはここを1問も落とさないようにしたい。
(1)剰余の定理
解答

解説
多項式の割り算に関する問題。処理は次の通りだ。

今回の[2]の処理は「各因数の余りを調べる」という形だ。
今回は上記の処理だったが、多項式の割り算(余り)に関する問題の解法は全て把握しておこう。
(2)余事象の確率
解答

解説
条件の「または」から余事象を考えた。
余事象でなくても確率の和として表せる。
どちらのアプローチが有効かは場合の数を考えた時に少ない方で考えたい。
また、具体的な計算について「順番が確定しているもの」は「同一のものとみなす」という方法で解こう。
階乗(!)と組合せ(C)、どちらでも解けることは知っておこう。
(3)対数方程式
解答
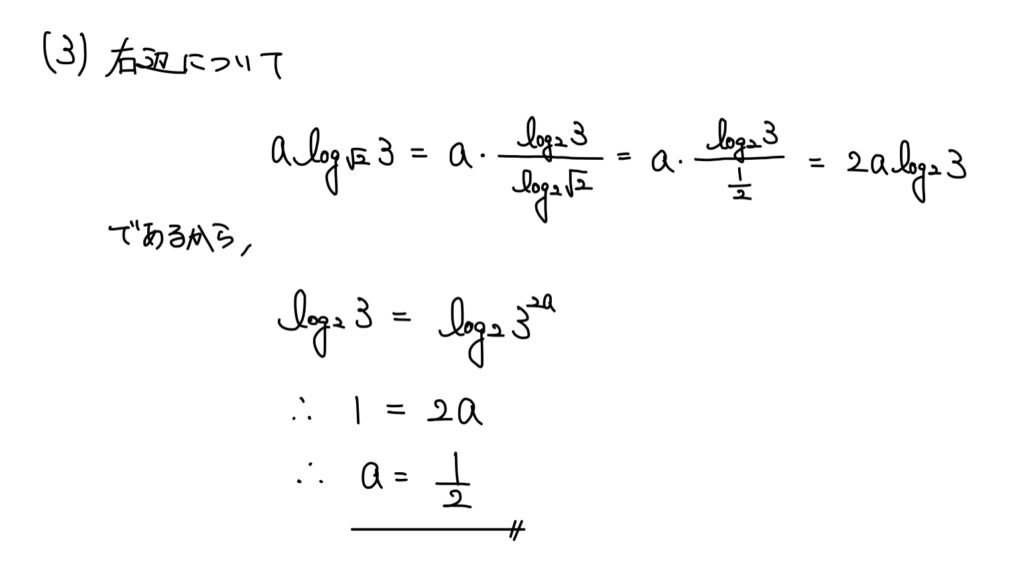
解説
対数方程式・不等式について、底が異なる場合は底の統一を考えよう。
今回は底さえ統一したら後は真数比較→指数比較で解答に至る。
今回は特に必要なかったが、指数・対数方程式での注意点として
- 0<(真数)
- 0<(底)<1,1<(底)
であることはしっかり抑えておきたい。
(4)平面ベクトルの内積
解答
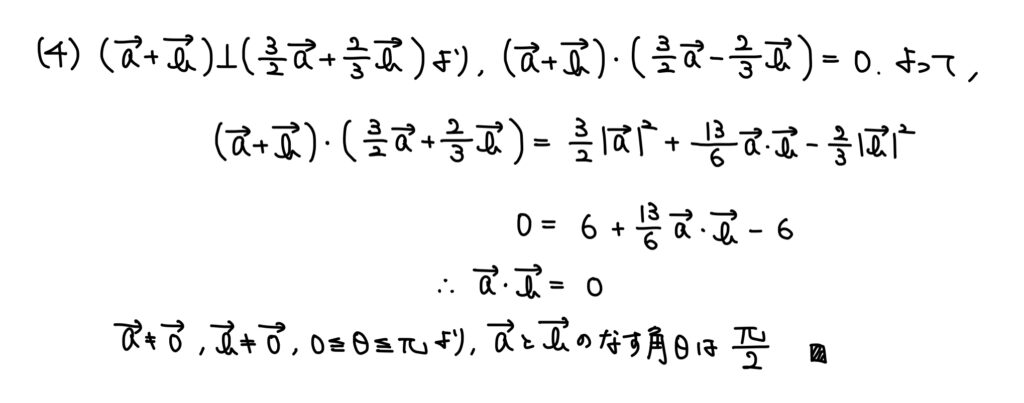
解説
2つのベクトルの垂直(なす角が90°)条件の問題。
ベクトル問題において角度が与えられたら内積を考える。
今回は「垂直ならば内積0」で解ける。
ベクトルの内積問題については以下の4つのアプローチを抑えておきたい。
- 定義(大きさとなす角)
- 成分(同一成分の積の和)
- 大きさの2乗
- 正射影
ベクトル道場シリーズの記事でベクトル問題は扱っているため、そちらも確認してもらいたい。
(5)特性方程式を利用する漸化式
解答

解説
今回は特性方程式を利用するタイプの数列の一般項を求める問題。
特性方程式を用いると分かっていれば等比の形に持っていくという流れだ。
漸化式は型が決まっているため、今回のように一般項を求めるだけの問題であればどんな型であれ解けるようにしておきたいところだ。
(6)積分方程式
解答
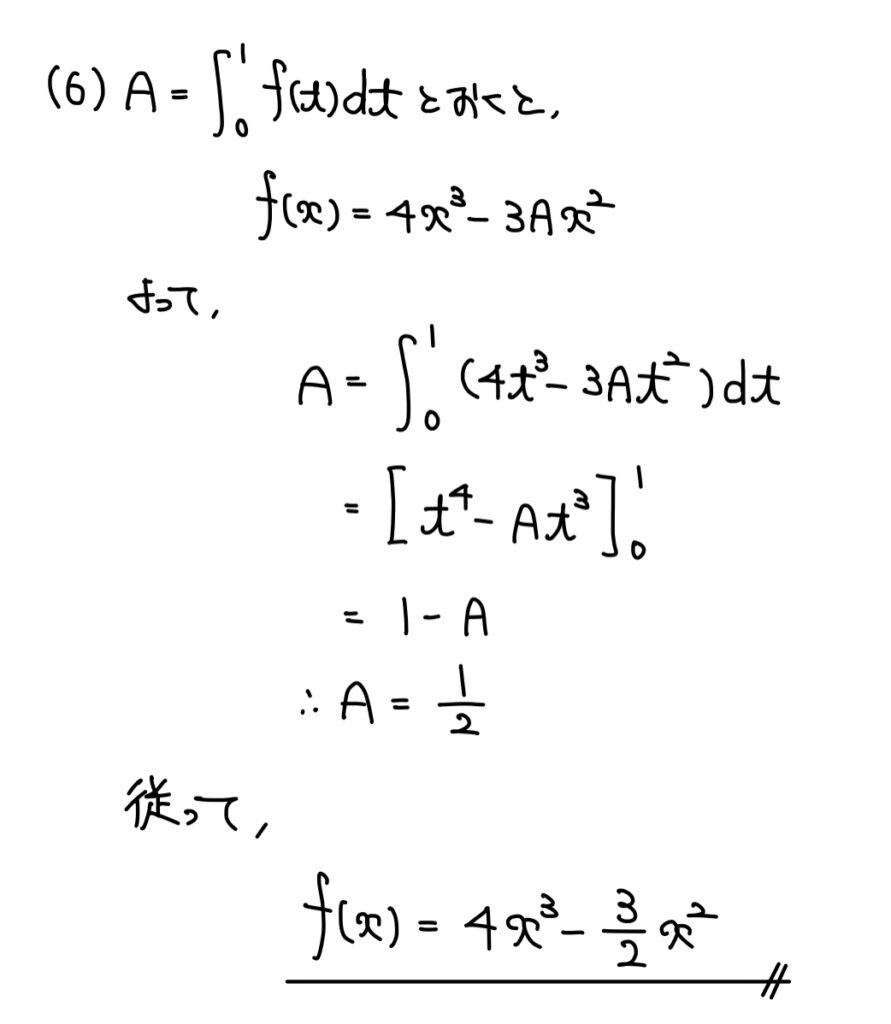
解説
積分方程式に関する問題。
区間が定数の場合は「A=(積分)」という形でおいて定数として扱えば良い。
区間が変数の場合は「①微分して区間の変数代入,②同一区間にして(積分値)=0」という形での処理を考える。
今回は区間が0から1のため「A=(積分)」という形でおいて定数扱いをすれば良い。
発想としては上記で、実際の処理は解答の通り。
さいごに
難易度としては、問題自体は教科書レベルだ。
合格者はほぼほぼ満点を取っているのではないか、という印象だ。
実際この学部の受験を意識している人は多くても1問ミス程度にしておきたい。
解けなかった人は基本問題を中心に演習を積んでいこう。
解けたけれどちょっと悩んだという人は日東駒専の過去問などが良いかもしれない。
余裕で解けた人はGMARCHの過去問を解いていこう。
自分としてはもっと単元が絡み合った問題の方が楽しいため、あまり面白さは感じなかった。
理工学部の問題も近々解きたい。



コメント