2020年度 富山大学の過去問を解いたので解答・解説記事をしていく。
今回の解答・解説は理系の前期入試を扱っていることには注意してもらいたい。(文系及び後期入試ではない)
早速見ていこう。
問題(大問3)
目安時間:40分
2020年度 富山大学 前期日程 理学部 数学
[ https://www.u-toyama.ac.jp/wp/wp-content/uploads/02zenki-05.pdf ]
※上記URL:国立大学法人富山大学HP 過去問ページより 2020年度 前期日程 理学部数学
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。
参考URL『国立大学法人富山大学HP-過去問題-』
https://www.u-toyama.ac.jp/admission/undergraduate-exam/past_exams/
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
富山大学は偏差値47.5〜62.5の国立大学(2021年6月3日時点 パスナビ調べ)。
最低偏差値の工学部と最高偏差値の医学部を合わせた偏差値のため,全然参考にはならない。(工学部を下に見ているわけではない)
問題としての難易度はGMARCH程度だろうか。
完答を目指すとなると大問3つの中では最も難しいのではないだろうか。
その根拠は積分を含む方程式という単元と(4)の解法の発想にある。
とりあえず(4)の(ア)までは比較的正答しやすそうなのでそこまで頑張りたい。
(4)は(イ)の方針が立たなかったらとりあえず時間内は飛ばしてもよいかもしれない。
とはいえ、超難問かというとそうではなく、小問からの流れを含めて発想が思い付くかどうかだ。
大問3は小問4つで構成されている。
やれる計算を着実に行いながら誘導を意識していこう。
(1)定積分を含む関数
解答

解説
ここはこの大問の中でも基本問題。
積分区間が関数となっているため、微分する際には積の微分&合成関数の微分となる。
解答の青い太枠内の知識さえあれば、あとは地道に計算していくのみ。
あまり多い問題でもないように思うため、ここでしっかり把握しておこう。
(2)定積分を含む関数
解答

解説
(1)と全く同様。使う知識は(1)解答の青い太枠内のみ。
積&合成関数の微分を着実に計算していく。
(3)定積分を含む関数
解答
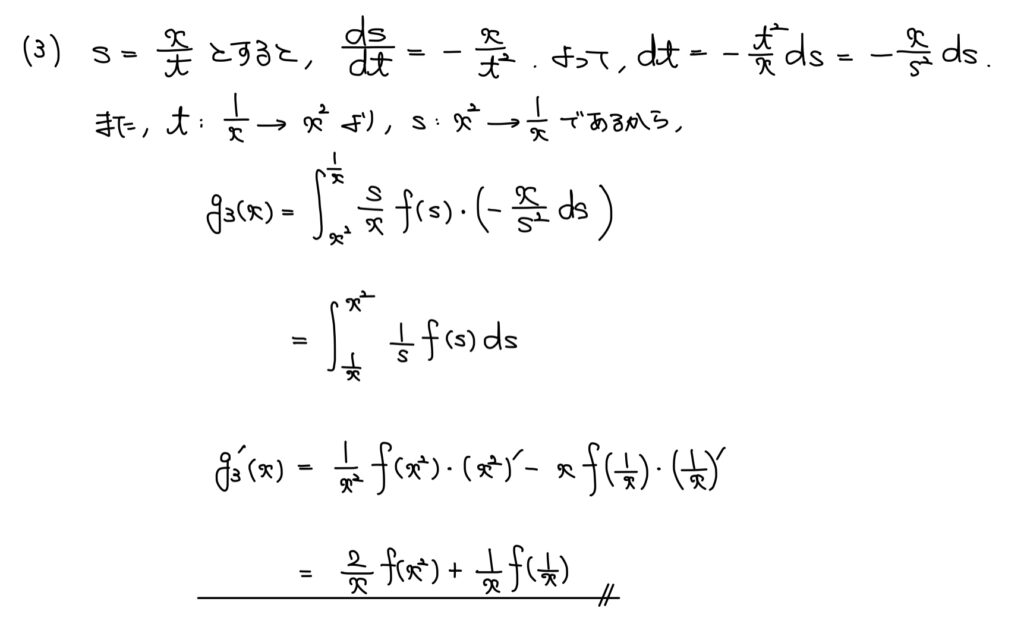
解説
よく分からない形は知っている形に持っていく。
(2)の流れから(2)と比較しながらfの変数部分がよく分からない形になっていることに注目。
知っている形にするために置換を考える。
置換後は(1),(2)と同じ計算方法。
(4)不等式の証明・方程式の解
解答

解説
(ア)不等式の証明
条件が与えられているため、どうなっているか具体化してみる。
とりあえずの目標は「f(1/x)を消去してf(x2)の不等式を作る」として、式変形をしていく。
2つの不等式を得られたとき、
- 和や差の2式 → 2式の加減(文字消去)
- 積や商の2式 → 掛け算結果の正負の利用(場合分け)
という思考は持っておきたい。
(イ)方程式の解
今までの流れを踏まえて証明していく。
まず直近に証明した(ア)の結果は扱うかもしれないと考え、何か手掛かりがないか考える。
すると、x>1での話が展開されていることを考え、f(x2)からf(x)を作ることを考える。
その際に、仮定のおかげもあり不等式がf(x)でも成立していることに気付き、立式ができる。
次に、0<x<1の範囲をどうしようかと悩むわけだが、今の流れやこれまでの流れ(扱える不等式)に目を向けるとf(1/x)でも同じ操作をしたらよいという思いに至り立式ができる。
あとは中間値の定理のようなイメージで、x=1でy=f(x)とx軸とが交点を持つことが分かる。
実際の証明は連続関数であることからx=1への右方極限と左方極限が一致することで示せる。
他に交点がないかという点に関しては、x>1で常にf(x)>0が成り立つためx=1のみが解であることが分かる。
さいごに
公式の模範解答はこちら
https://www.u-toyama.ac.jp/wp/wp-content/uploads/r02_A-06.pdf
参考URL:国立大学法人富山大学HP 「過去問題」ページより 令和2年度 前期日程 理学部数学 解答例等
難易度としては、東京の私立で言えばGMARCHを受ける人でも合成関数というところでのミス、(4)(イ)の方針決めというところでは悩むのではないかという印象だ。
積分方程式の指針についても今回の問題をきっかけにして、しっかりと練習を積んでいくとよいだろう。
解けなかった人はしっかりとこれからもトレーニングを積んでいこう。
解けた人はしっかりとした方針決めができているため、もう少し偏差値の高い大学の過去問を解いてみても良いかもしれない。
自分としてはやっぱりこういった「さっき証明したものは使ってね」「難しく(抽象化)なっても意外とさっき示したこととやること変わらないでしょ」といった問題がとても好きだ。
国公立の形式が好きなのかもしれない。
これからも国公立の問題は多めに解いていこうかな。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント