2020年度 金沢大学の過去問を解いたので解答・解説をしていく。
今回解答・解説をするにあたり、前期日程を扱っている点には注意してもらいたい。(後期日程ではない)
早速見ていこう。
問題(大問3)
目安時間:30分
2020年度 金沢大学 前期日程 数学(理系)
[ https://www.kanazawa-u.ac.jp/wp-content/uploads/2020/04/02-2-2sugaku_rikei_zenki.pdf ]
※上記URL:国立大学法人金沢大学HP 「過去問題及び正解・解答例」ページより 令和2年度入試 前期日程 理系数学
※過去3年分が公式HP(下記URL)から閲覧できます。2020年度分が掲載終了している可能性もあります。
参考URL『国立大学法人金沢大学HP-過去問題-』
https://www.kanazawa-u.ac.jp/education/admission/kakomondai
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
金沢大学は偏差値50.0〜65.0の国立大学(2021年6月17日時点 パスナビ調べ)。
大問3は円すいの体積の最大・最小問題。
難易度的にはこの年では大問4の次に難しいのではないだろうか。
というのも、状況の整理や変数の設定というところが悩みそうだ。
こういった問題の多くは正しく変数設定ができると問題自体はそんなに難しくはない。
ゆえに、変数の設定が重要といえる。
体積の最大・最小というところから体積を関数で表して、関数の最大・最小の話にもっていけばいい。
解説では、関数の表し方に注目して自分なりに説明した。
細かく話したので話が長くなってしまった。
その分、少しでも変数設定について皆さんの一助となれば幸いだ。
大問3(微分法と図形、関数の最大・最小)
解答


解説
今回の大問を見て難しく感じるポイントは何をしたらよいのか掴みづらいところにある。
条件を見ると辺の長さ(2点間の距離)がいくつかと、円の接点や二等辺三角形の垂線など垂直条件をもらっていることには気付くだろう。
けれど、何をしていいか分からない、となるのではないだろうか。
何をしたらいいのか分からない時は、まずゴールを見据えよう。
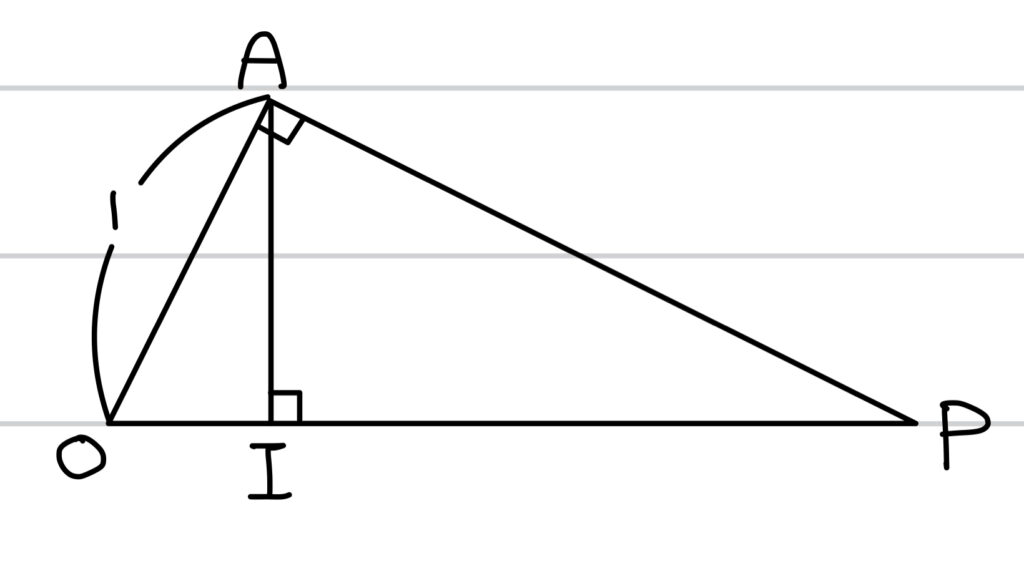
何を答えたらよいのか、今回でいえば△OABを直線OPのまわりに1回転してできる円すいの体積の最大・最小だ。
つまり、今回最初に注目すべきは回転する前の△OABだ。
△OABを考察することで回転体の様子が分かり、その後の解答に繋がる。これは想像できるだろう。
では、△OABのどこに注目すればよいか。
それは円すいの体積に繋がる部分、つまり、底面積の半径となるABの中点 I と高さのOIだ。
これらを求められるように変数の設定をしていけばよい。
変数を設定するときの鉄則は以下の2つだ。
- 変域を必ず確認すること
- 文字の個数はなるべく少なくすること
では、実際どこを文字でおくか。
改めて条件を考えてみると前述の通り、円の接点やAB⊥OPなど明らかに垂直条件が多い。
最初に条件チェックをしなかった人はこのタイミングで確認してもよいだろう。
最初に述べた通り、辺の長さ(2点間の距離)がいくつかと、円の接点や二等辺三角形の垂線など垂直条件をもらっていることに気付こう。
特に円の接点なんかはほぼ確実に垂直を考慮して扱う。
また、確信的なのが以下の形を見た時だ。
この形は超有名な直角で相似が扱える形なのだ。
そこで自分は相似比を使えるのではないかと考えた。
どこを文字で置いてもいいが、最終的に重要なのは円すいの底面積の半径AIだ。
どこかを文字で置いて、三平方の定理や相似を扱いながらAIを求めにいこう。
そして、円すいの高さOIもこの図形を用いて考えられる。
相似比から考えていけばよい。
変数で表すことができれば、円すいの体積をその変数を用いて表すことができる。
こうして体積の最大・最小問題を、関数の最大・最小問題の変換に成功する。
分数関数の最大・最小としてもよいが、自分は整関数の最大・最小の方が扱いやすいため、更に変数変換をしま。
ここからはグッと楽になってよくある形の最大・最小問題だ。
微分して増減表という流れだ。
最後に、Pの存在範囲の図示だが、まず前提として△STUの内部であることだ。
次に、最大と最小の場合を考えるとOPの距離が一定の時であるからPは円周上となる。
あとは半径が分かればよくて、それは増減表を見て考えればよい。
さいごに
公式の模範解答はこちら
https://www.kanazawa-u.ac.jp/wp-content/uploads/2020/04/02-2-02sugaku_rikei_zenki.pdf
参考URL:国立大学法人金沢大学HP 『過去問題及び正解・解答例』より令和2年度 前期日程 数学(理系) 正解・解答例
問題の難易度は、私立で例えればGMARCHレベルというのが妥当だろう。
解答の1行目と求めたいところと繋げるのに困る問題ではあるが、そこさえ乗り越えれば難しくない問題だ。
変数設定に注力する問題だと思い、復習はその点を重要視すればよいだろう。
個人的に苦手な
楽しみながら学んでいこう。



コメント