2020年度 中央大学の過去問を解いたので解答・解説記事をしていく。
今回解答・解説をしていくのは経済学部の一般入試を扱っているのには注意してもらいたい。(理工学部の入試ではない)
早速見ていこう。
問題(大問3)

まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
全体概評
中央大学は偏差値60.0〜62.5の私立大学(2021年6月1日時点 パスナビ調べ)。
難易度としては難問ではなく、典型的な問題と言える。
大問3は小問3つで構成されている。
基礎的な問題と言えるため、確実に点を取っておきたい問題であった。
(1)接線の方程式
解答
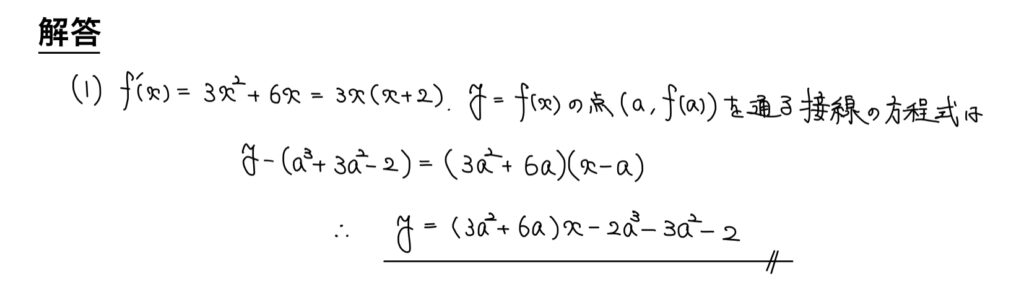
解説
接線の方程式を求める問題のよくある出題形式は以下の2つ。
- 「接点における」接線の方程式を求めよ
- 「ある点を通る」接線の方程式を求めよ
1.は接点が分かっているため、接線の方程式に代入して終了。
2.は接線の方程式を作りたいが接点が分からない。
そこで接点を( t , f(t) )と設定してひとまず接線の方程式を作る。
その後通る点を代入してtを求めることで接線の方程式を得る。
今回は文字定数とはいえ、接点が与えられているため1.の処理で直ちに求めることができる。
これは受験生の大半が正解する問題と思われるため、ケアレスミスもないよう必ず答えられるようにしておきたい。
(2)直線を通る点
解答
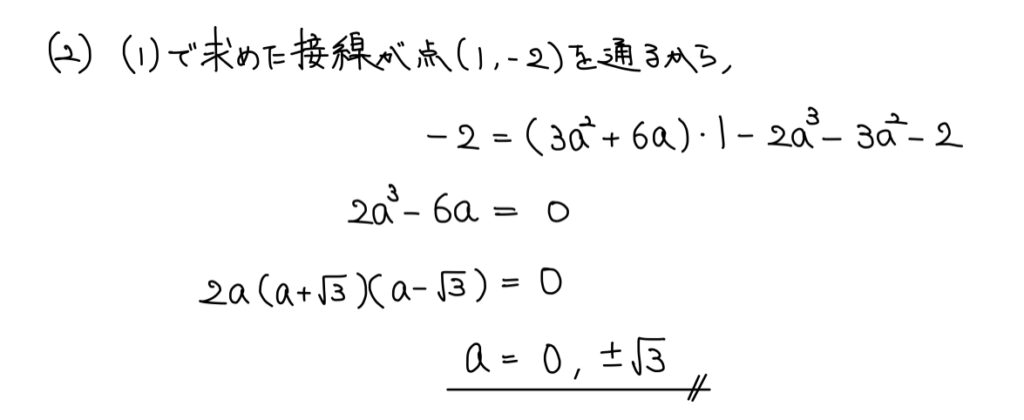
解説
通る点は代入可能。
(1)で求めた接線の方程式に代入して求めればいい。
(3)2つの関数の交点の個数
解答
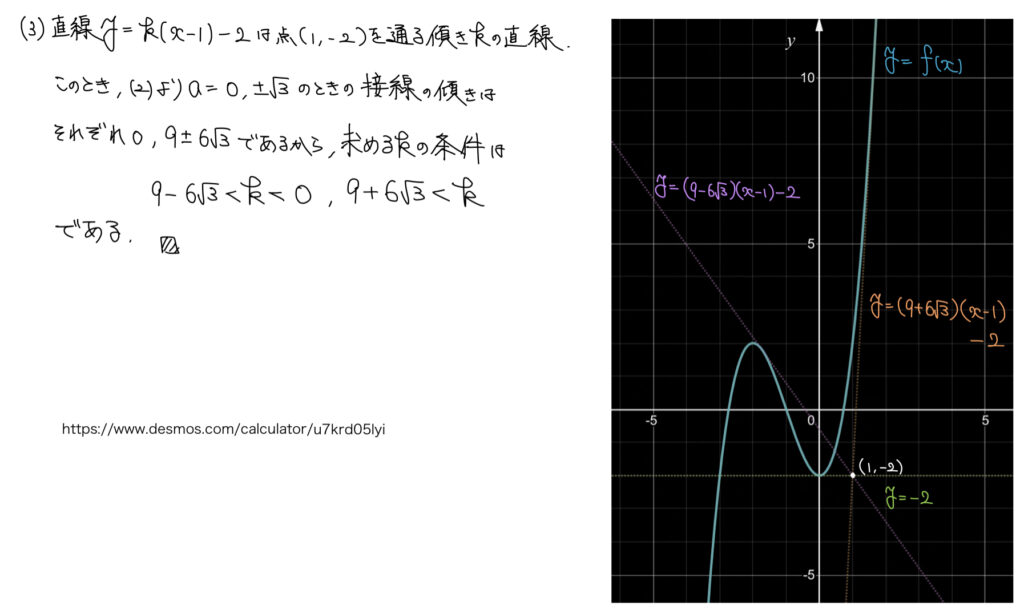
グラフURL → https://www.desmos.com/calculator/u7krd05lyi
※点(1,-2)を通る傾きkの直線のkの値を変えてみよう
解説
2つのグラフの交点の個数が3個になればよいという問題。
文字定数kを分離して分数関数と定数関数の交点の個数として話を言い換えても良いが、今回はわざわざ(2)で点(1,-2)を通る接線を求めているためそれを利用するのがいいだろう。
y=f(x)のグラフをかいて位置を確認して、あとは傾きkを動かしながら交点が3つになるような条件を考えていけばよい。
さいごに
難易度としては、(1),(2)は基礎、(3)は標準といったところだろうか。
印象として(1),(2)は合格者はほぼほぼ全員正解してるだろう、(3)は合否の分け目となりそう、といった感じだ。
(3)も問題集には似たような問題があるのではないだろうか。
(1),(2)が解けなかった人はまず基礎的なところから見直す必要がある。
(3)が解けなかった人は今回しっかり理解して、類題を探してトレーニングを積んでいこう。
個人的にはテンプレ問題だったので特に学びはなかった。
とはいえ、(3)が定数分離でも解けることを確認しておくことで違った解法の仕方を学ぶこともできて少し有意義になりそうではある



コメント