2020年度日本大学の過去問を解いたので解答・解説をしていく。
2020年度N方式の全ての問題を解き、文系が大問1〜4、理系が大問5〜10であることには注意してもらいたい。
それでは、早速見ていこう。
問題(大問8)
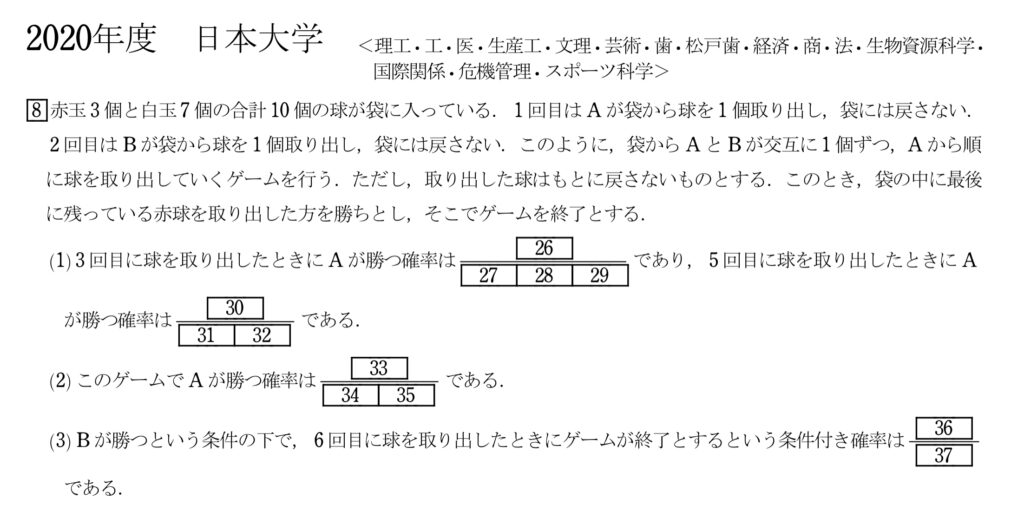
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
日本大学は偏差値35.0〜67.5の私立大学(2021年7月7日時点 パスナビ調べ)。
偏差値自体は35.0の工学部から67.5の医学部まで幅広いため、あまり偏差値はあまり参考にならない。
教科書レベルの基本的な問題だ。
GMARCH以上や中堅国立を志望する人は基礎力を定着させるためにもしっかり完答できるようにしておこう。
(1)場合の数と確率
解答

解説
「3回目にAが球を取り出したときにAが勝つ確率」は言い換えれば「3回連続で赤球を取り出す確率」と言える。
奇数回でAが球を取り出し、偶数回でBが球を取り出すため、誰が球を取り出すかを考える必要はなく、何回目で取り出すかだけ考えればよい。
ゆえに、今回の問題は「誰が取り出すか」ではなく、「何回目で取り出すか」を考えていく。
また、「5回目にAが球を取り出したときにAが勝つ確率」は言い換えれば「4回目までで赤球が2個、白球が2個取り出していて、5回目に赤球を取り出す確率」と言える。
よって、4回目までと5回目で分けて考えればよい。
(2)確率の加法定理
解答

解説
(1)の流れからやることは全く同様。
「7回目にAが球を取り出したときにAが勝つ確率」は言い換えれば「6回目までで赤球が2個、白球が4個取り出していて、7回目に赤球を取り出す確率」と言える。
「9回目にAが球を取り出したときにAが勝つ確率」は言い換えれば「8回目までで赤球が2個、白球が6個取り出していて、9回目に赤球を取り出す確率」と言える。
求め方は(1)同様。
これで全てのAが勝つパターンを考えたため、足せば良い。
(3)余事象の確率、条件付き確率
解答
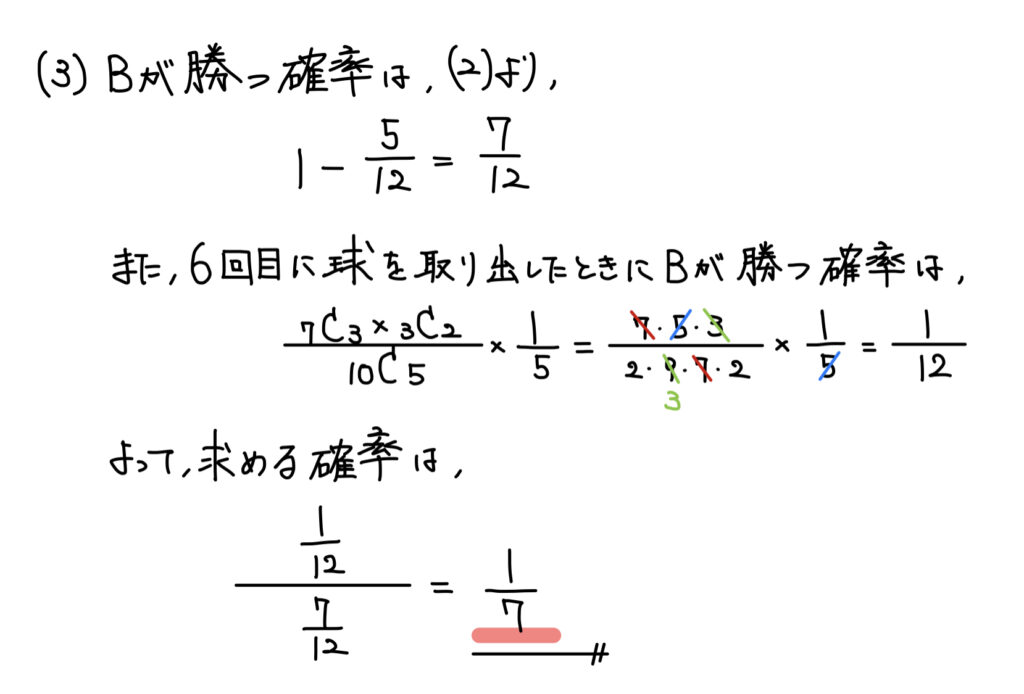
解説
このゲームで引き分けはあり得ないため、Bの勝つ確率はAの勝つ確率の余事象として求めることができる。…①
また、「6回目に球を取り出したときにゲームが終了する確率」は言い換えれば「5回目までで赤球が2個、白球が3個取り出していて、6回目に赤球を取り出す確率」と言える。…②
あとは、①を分母、②を分子として条件付き確率を求めれば良い。
さいごに
確率が苦手という人の多くに「何をしていいか分からない」、「どの公式を使うのか分かりづらい」というのがある。
個人的には、確率で公式を適用させたいというのが苦手意識の原因のように思う。
場合の数、確率は状況把握が何よりも重要だ。
問題集を一周してある程度理解しているのに演習で解けないという人は問題文の言い換えができていないことが多い。
問題文を見て、(あの問題と似てる!)と類似の問題と言い換える訓練が必要だ。
状況把握ができると「これって書かれ方違うけど、この問題と言ってること一緒だ」と思えるようになる。
こうなってくると問題文に騙されることなく安定してくる。
苦手な人こそ状況把握。
そういった目線で訓練してみてもらいたい。
一緒に頑張ろう。



コメント