2020年度日本大学の過去問を解いたので解答・解説をしていく。
2020年度N方式の全ての問題を解き、文系が大問1〜4、理系が大問5〜10であることには注意してもらいたい。
それでは、早速見ていこう。
問題(大問9)
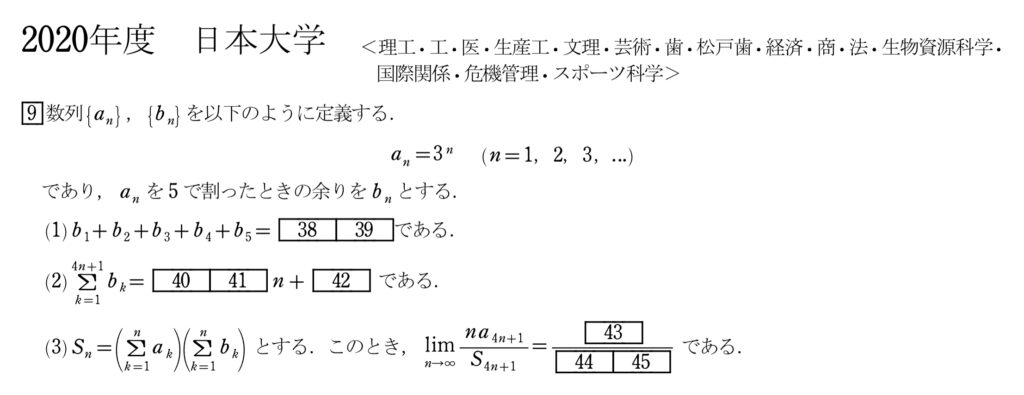
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
日本大学は偏差値35.0〜67.5の私立大学(2021年7月7日時点 パスナビ調べ)。
偏差値自体は35.0の工学部から67.5の医学部まで幅広いため、あまり偏差値はあまり参考にならない。
問題全体を通してみると、個人的にはこの大問が一番難易度が高いように思う。
とはいえ、超難問というわけではなく、基礎知識で解ける問題だ。
GMARCH以上や中堅国立を志望する人は基礎力を定着させるためにもしっかり完答できるようにしておこう。
(1)剰余の分類
解答
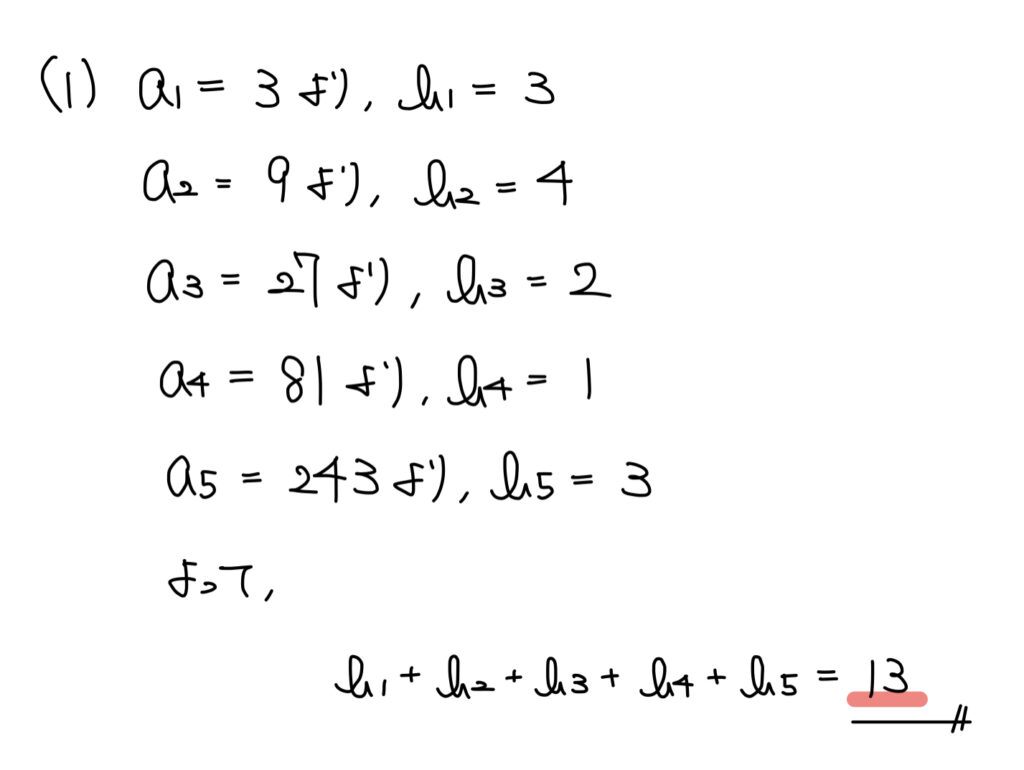
解説
問題文から特殊な発想が出なくても、具体化・実験で十分に答えが求められる。
これを間違える人はまずいないだろう。
(2)剰余の分類、数列の和
解答

解説
4nという形は馴染みがなく、ここで撃沈した方が多いように思う。
しかし、(1)の誘導とわざわざ4nにしているというところから察しはつく。
合同式を理解している人は察しがつきやすいとは思うが、(1)から余りは1、3、4、2の周期で現れることが分かり、今回の回答に至る。
余りの周期性に気付かなければ、この問題を解くのは難しいため、余りには周期性があるということだけでもこの問題から得ておこう。
この周期性に気付いたあとは、余りを4個で1組として考えると良い。
4個の和は10で、それをn個分足すため4nとして考えて解く。
(3)数列の極限
解答

解説
形はよく分からないが、とりあえずできる計算をするしかない。
S4n+1を求めて、結論の形を調べよう。
すると、指数関数と整関数の積の形が見えているため、nを無限への発散でのキーマンは指数関数であることが分かる(指数関数の方が整関数より発散速度が速いため)
あとは割り算の形にして極限を考えれば良い。
見慣れない形でも手を動かすことで見えてくるため、諦めないようにしたいところだ。
さいごに
問題集によくある形の問題とはいえない問題のように思う。
しかし、問われていること自体は基本的な部分も多いため、しっかり要素を分解して具体化・実験していけば見えてくる問題だ。
見慣れない形でもやれることはやっていこう。
また、この問題を解けなくても正答率は他の問題に比べてそんなに高くないであろうため、切り替えて他の問題を解けばよい。
解ける問題で確実に解く、ということを徹底するとともに、余りの周期性や指数型の極限などをここでしっかり学習していこう。
出来ない問題こそ成長の種だ。



コメント