2020年度 日本大学入試問題を解いたので、振り返りと解法の確認をまとめておこうと思う。
解説という訳ではなく、あくまで自分用のまとめみたいなものだ。
各大問の詳細な解答・解説は別記事で行っているのでそちらを参考にしてもらいたい。
リンクは各大問の概評に貼ってある。
この記事はあくまで大問ごとの大きな基本方針を述べるに留める。その問いから学べることの言語化に注力している。
また、タイトルで「理系」と紹介したが厳密ではない。
細かい受験問題は学部・学科によって細分化されているため、受験生は本当に自身が受けるのが大問1〜4なのか、大問5〜10なのかは要確認してもらいたい。
では、まずは問題から見ていこう。
問題(理系は5〜10)
解くのを楽しみにしてる方は是非解いてみてほしい。
楽しめると思います。
では、解説していこう。
全体
先に問題形式などの確認をしておこう。
| 時間 | 60分(大問5〜10) |
| 入試科目 | 数学Ⅰ・Ⅱ・Ⅲ・A・B |
| 出題形式 | マーク |
| 問題数 | 大問6つ |
次に概評。
全体を通して教科書の問や節末問題レベルといったところだろうか。
チャート式で言えば難易度はコンパスマーク3つ以下といったレベルだろうか。
学校で問題集が配布されている人達は、おそらくそこに今回の問題の類題が記載されているだろう。
どの問題集でも類題がある基本的な問題で構成されている。
日大志望者は、分厚くない問題集を1冊しっかり行えば解けるようになるのではないだろうか。
大問6問で試験時間が60分。
時間的には結構厳しめで、解法に迷っている時間はない。
さて、それでは各大問の解説をしていこう。
大問5概評
大問5は様々な単元が集まった問題だ。
単元も様々で、広く基本的なことができることが問われる。
一問一問基本的な解法になるため、しっかり知っておきたい。
解答・解説 → 「101話 2020 日本大学 過去問大問1【解答解説】」
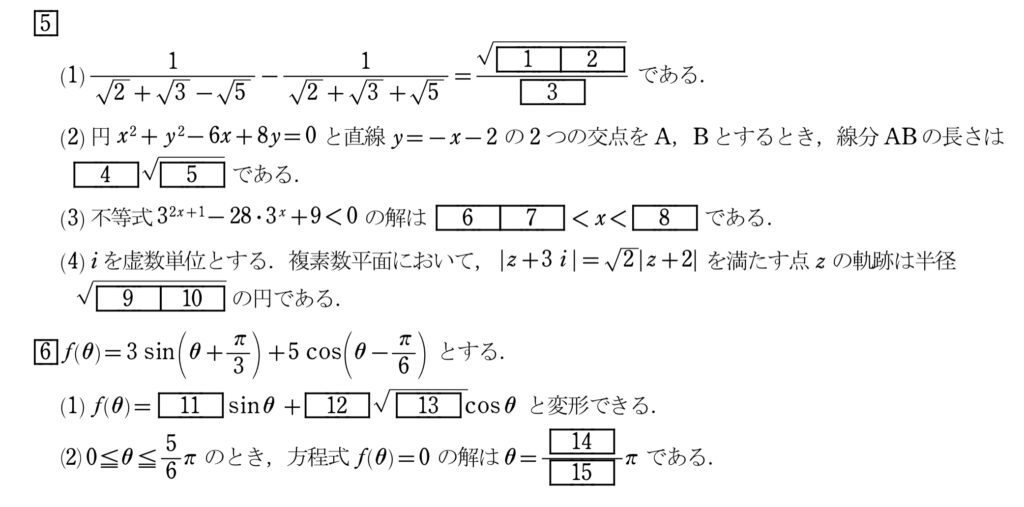
(1)分母の有理化
3項の分母の有理化は2項をまとめて1つのカタマリとして見て、2項の有理化として扱う。
2項の分母の有理化は和と差の積の利用。
(2)解と係数の関係、2点間の距離
交点を求めるためには連立方程式を解けばいい。
2つの解がそれぞれAとBのx座標に対応するわけだが、どっちの値がどっちの点に対応するかはあまり考えなくても良い。
どっちがAでどっちがBでも距離は変わらないからだ。
どっちでもいいというときは「一般性を失われない」と述べるとよい。
また、最後に求めるものが何かを見据えておくと対称式のアプローチが思い付く。
(3)指数不等式
指数方程式は素数の累乗を文字で置いて、整関数へと言い換えるのが定石だ。
文字でおくときは必ず新しい文字の変域に注意することに注意しよう。
今回は2次整関数の不等式へと話を持ち込るため、因数分解で解けばいい。
最後にtからxへ文字を戻してあげれば答えを得る。
(4)複素数と図形
複素数で大きさ同士の等式は2乗して展開していこう。
あとは平方完成のイメージを持ちながら式変形をして行けばよい。
こういった式変形は必ずどの問題集にもある典型問題のため、しっかり抑えておこう。
大問6概評
大問6は三角関数の加法定理や合成に関する基本的な問題だ。
どういう時に加法定理を用いて、どういう時に三角比の合成を行うか整理しておこう。
一問一問基本的な解法になるため、しっかり知っておきたい。
解答・解説 → 「107話 2020 日本大学 過去問大問6【解答解説】」
(1)三角関数の加法定理
加法定理を使えば直ちに答えを得る。
変数部分が和や差の場合は加法定理を考えよう。
符号ミスには注意だ。
(2)三角関数の合成、三角方程式
(1)を利用して合成を考える。
合成は「同角一次式」(角が等しく次数が1の三角関数)の時に有効だ。
合成するとsinの方程式となるため計算することができる。
同値記号を使う際には一般角で答えるように気を付けよう。
大問7概評
大問7は平面ベクトルの問題。
角度と内積をについて十分な情報量があるため、大きさも位置ベクトルも自由に求めることができる。
これも基本的な問題であるため、しっかり抑えておこう。
解答・解説 → 「108話 2020 日本大学 過去問大問7【解答解説】」
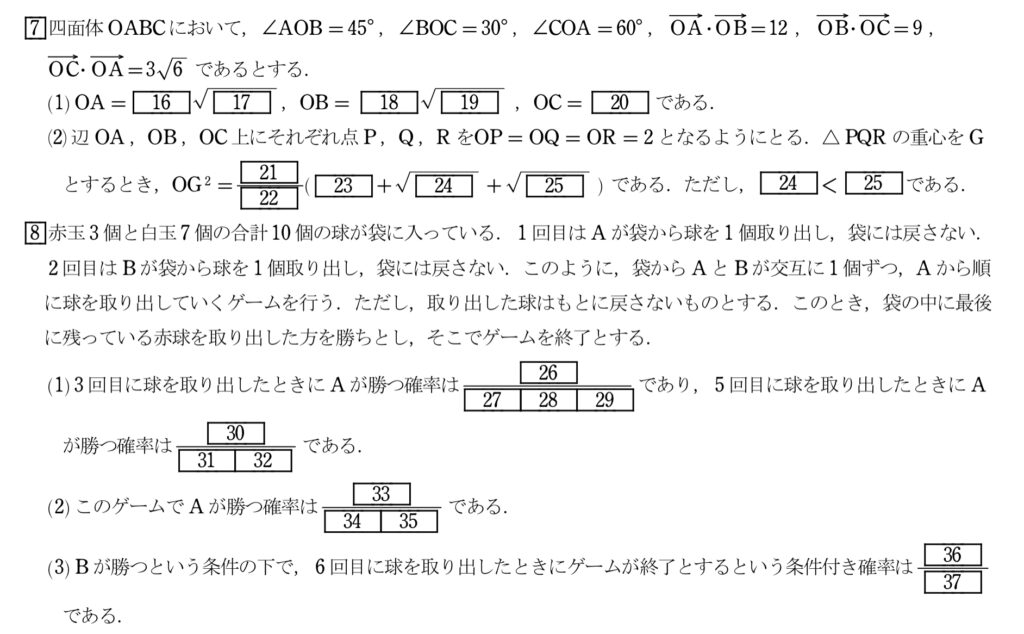
(1)平面ベクトルの大きさ、内積
角度と内積が十分な情報量与えられているので、内積から大きさを求めにいこう。
ab=○、bc=△、ca=□が分かる状況では、全て足掛けて(abc)2=○△□とするのが有効。
(2)平面の位置ベクトル
3点P、Q、Rについて大きさの情報があるため、内積の情報を求めておこう。
大きさと内積の情報が揃ってベクトルでできないことはない。
大きさと内積をともに使うためには大きさの2乗が有効。
求める重心との距離も2乗で問われているためとても都合がいい。
大問8概評
大問8は確率(特に条件付き確率)に関する問題
条件付き確率が苦手という人は多いだろう。
今回は基本的な知識と発想で解けるためとても良い演習になるのではないだろうか。
解答・解説 → 「109話 2020 日本大学 過去問大問8【解答解説】」
(1)場合の数と確率
「3回目にAが球を取り出したときにAが勝つ確率」は言い換えれば「3回連続で赤球を取り出す確率」と言える。
奇数回でAが球を取り出し、偶数回でBが球を取り出すため、誰が球を取り出すかを考える必要はなく、何回目で取り出すかだけ考えればよい。
ゆえに、今回の問題は「誰が取り出すか」ではなく、「何回目で取り出すか」を考えていく。
また、「5回目にAが球を取り出したときにAが勝つ確率」は言い換えれば「4回目までで赤球が2個、白球が2個取り出していて、5回目に赤球を取り出す確率」と言える。
よって、4回目までと5回目で分けて考えればよい。
(2)確率の加法定理
(1)の流れからやることは全く同様。
「7回目にAが球を取り出したときにAが勝つ確率」は言い換えれば「6回目までで赤球が2個、白球が4個取り出していて、7回目に赤球を取り出す確率」と言える。
「9回目にAが球を取り出したときにAが勝つ確率」は言い換えれば「8回目までで赤球が2個、白球が6個取り出していて、9回目に赤球を取り出す確率」と言える。
求め方は(1)同様。
これで全てのAが勝つパターンを考えたため、足せば良い。
(3)余事象の確率、条件付き確率
このゲームで引き分けはあり得ないため、Bの勝つ確率はAの勝つ確率の余事象として求めることができる。…①
また、「6回目に球を取り出したときにゲームが終了する確率」は言い換えれば「5回目までで赤球が2個、白球が3個取り出していて、6回目に赤球を取り出す確率」と言える。…②
あとは、①を分母、②を分子として条件付き確率を求めれば良い。
大問9概評
大問9は余りの分類と数列、級数に関する問題。
理系の6問の中で一番完答率が低そうだ。
しかし、(2)までの正答率は非常に高いことが予想され、高得点者か否かを分けるような問題とも言える。
(2)まではしっかり解けるようにしておこう。
解答・解説 → 「110話 2020 日本大学 過去問大問9【解答解説】」
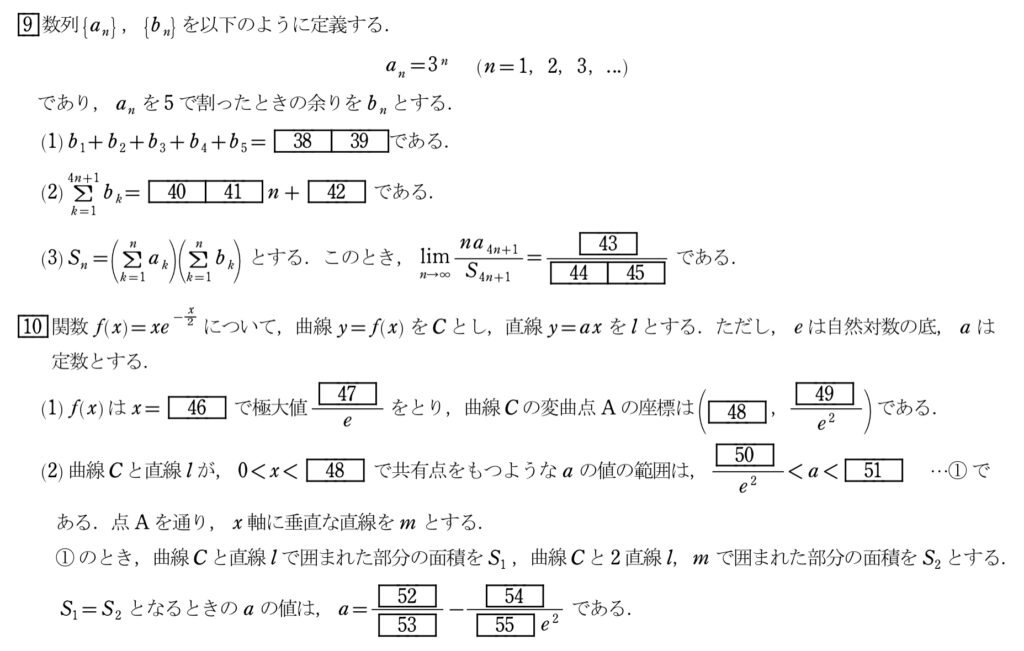
(1)剰余の分類
問題文から特殊な発想が出なくても、具体化・実験で十分に答えが求められる。
代入して調べるだけのため、これを間違える人は少ないだろう。
(2)剰余の分類、数列の和
4nという形は馴染みがなく、ここで撃沈した方が多いように思う。
しかし、(1)の誘導とわざわざ4nにしているというところから察しはつく。
合同式を理解している人は察しがつきやすいとは思うが、(1)から余りは1、3、4、2の周期で現れることが分かり、今回の回答に至る。
余りの周期性に気付かなければ、この問題を解くのは難しいため、余りには周期性があるということだけでもこの問題から得ておこう。
この周期性に気付いたあとは、余りを4個で1組として考えると良い。
4個の和は10で、それをn個分足すため4nとして考えて解く。
(3)数列の極限
形はよく分からないが、とりあえずできる計算をするしかない。
S4n+1を求めて、結論の形を調べよう。
すると、指数関数と整関数の積の形が見えているため、nを無限への発散でのキーマンは指数関数であることが分かる(指数関数の方が整関数より発散速度が速いため)
あとは割り算の形にして極限を考えれば良い。
大問10概評
大問10は関数の極値、積分に関する問題。
極値とはどういう点か、変曲点とはどういう点か、しっかり説明できるようにしておこう。
積分は計算ミスに注意だ。
解答・解説 → 「111話 2020 日本大学 過去問10話【解答解説】」
(1)関数の極値・変曲点
極値、変曲点だけを考えるこの問題では必ずしも増減表が必要というわけではないが、この後の積分や図形理解を考えるためにも増減表は書いておきたい。
極値は「f’の符号が変わる点」、変曲点は「f”の符号が変わる点」であることに注意しよう。
増減表がしっかり書けていれば正答できる問題だ。
(2)積分
積分は関数と区間が分かれば良い。
今回、関数は分かっているため、交点を求めて区間の確認をすれば良い。
区間が求めれられたら、位置関係「(上の関数)ー(下の関数)」で積分すれば良い。
さいごに
全ての大問を通して、「基本問題の解法の理解は出来ていますか?」ということが問われている。
単元も特に偏りがなく出題されているため、志望者は基礎問題をしっかり解くことを意識して学習していく他ない。
ざっくり数学ⅠA・ⅡB・Ⅲの学習を終えたら過去問を解いてみても良いかもしれない。
学んだ基本的な操作を視点を少し変えながら見ていくため、楽しい。
解いた方、お疲れ様でした。



コメント