2020年度北里大学の過去問を解いたので解答・解説をしていく。
今回は獣医学部獣医学科の問題を解いた。(理学部や獣医学部動物資源科学科、生命環境科学科ではないので注意)
それでは、早速見ていこう。
問題(大問2)
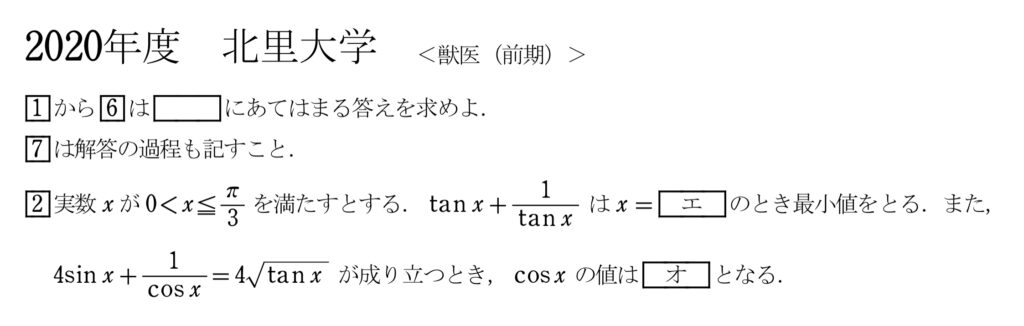
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
北里大学は偏差値40.0〜62.5の私立大学(2021年7月23日時点 パスナビ調べ)。
大問2は分数式・三角関数の最大・最小問題の問題だ。
まず、分数式の最大・最小で相加・相乗平均を疑うようにはしたい。
また、見たことがない形は見たことある形への変形(置換・同値変形)もしくは誘導にのることを考えられるようにしたい。
見たことがないから解けない、ではなく、ではどうするかに注目していこう。
大問2(分数式の最大・最小、三角関数)
解答

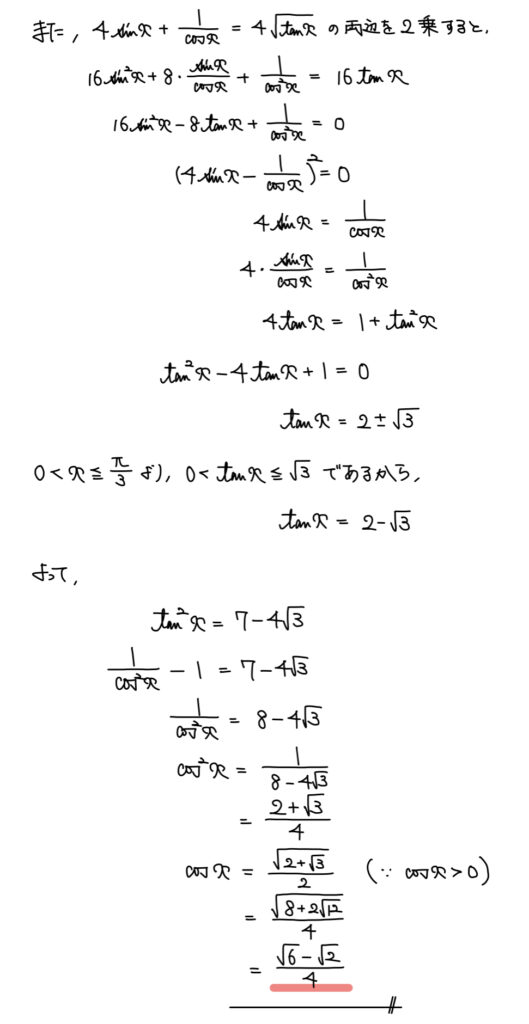
解説
分数式の最大・最小問題ではすぐに数Ⅲの分数式の増減表の作成を疑う前に、まずは相加・相乗平均を考えよう。
使えるか使えないかがすぐに判断つく上に、圧倒的に時短になるからだ。
相加・相乗平均を用いることができる条件として
- 相加・相乗平均を用いる2つの数が定義域や前提で正数になるような状況であること
- 相乗平均を考えた後に変数がなくなること
が挙げられる。これを調べることは容易のため、まずは相加・相乗平均を考えよう。
等号成立条件は相加・相乗平均を用いた2つの数が等しくなるときだ。
その後の三角方程式では、平方根からも考えられるが、2乗を考えよう。
平方根があることも2乗を考える大きな一因だが、そもそも三角比自体2乗ととても相性が良いため常に解法の候補としてなければいけない。
積分や三角方程式・不等式では2乗することはよくあるので知っておこう。
2乗後はsinでもcosでもtanでも何でもいいのでどれかに揃えよう。
最終的にcosが問われていることを踏まえて式変形していくと良い。
三角比は相互関係を用いればsin、cos、tanのどれにでも変形できるからそこは恐れる必要はない。
自分の求めたいものに向けて式変形を淡々としていこう。
最後に必ず第一象限であることは確認しよう。
さいごに
個人的には楽しい問題だった。
三角方程式は対策しやすいため、偏差値を考えると合格者のほとんどは解けていそうだ。
相加・相乗平均はふと忘れてしまうことがあるので注意しておこう。
北里大学、解いていてだいぶ好きかもしれない。
自分が受験生時代に出会っていたら受けていたかもしれない。
これからも楽しみながら解いていこう。



コメント