2020年度北里大学の過去問を解いたので解答・解説をしていく。
今回は獣医学部獣医学科の問題。(理学部や獣医学部動物資源科学科、生命環境科学科ではないので注意)
それでは、早速見ていこう。
問題(大問7)

まず、実際に解いてみて欲しい。
頑張って!
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
北里大学は偏差値40.0〜62.5の私立大学(2021年7月23日時点 パスナビ調べ)です。
大問7は2次関数で囲まれた面積と面積の最小値の問題。
2次関数の面積の中でも今回は定義域が変動するタイプ。
定義域が動こうが、軸が動こうが、頂点が動こうがやることは
- 平方完成して
- 簡単なグラフをかいて
- 求める面積の確認
という手順で解いていこう。
グラフを確認したら求める状況に漏れがないかを確認しながら、必要に応じて場合分けをしよう。
(1)2次関数で囲まれた面積
解答
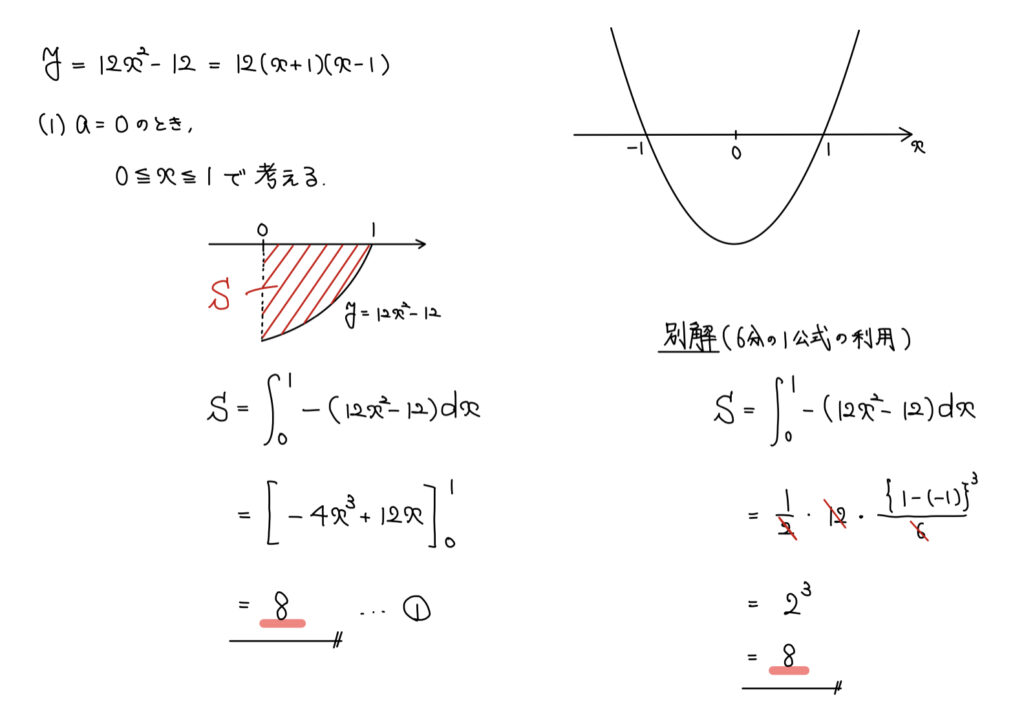
解説
a=0で定義域が固定されているので、変数aは気にせず2次関数の最大・最小問題を求めにいこう。
概評でも書いたが、
- 平方完成して
- 簡単なグラフをかいて
- 求める面積の確認
をすれば良いですね。
この問題においての注意点は、積分する際に関数とx軸との位置関係だろうか。
位置関係が「(上の関数)ー(下の関数)」で積分するようにしよう。
また、別解を記載しましたが、6分の1公式が有効なパターン(2次関数に直線で蓋の形)であるため、そちらの解答もできるようにしておこう。
(2)2次関数で囲まれた面積
解答
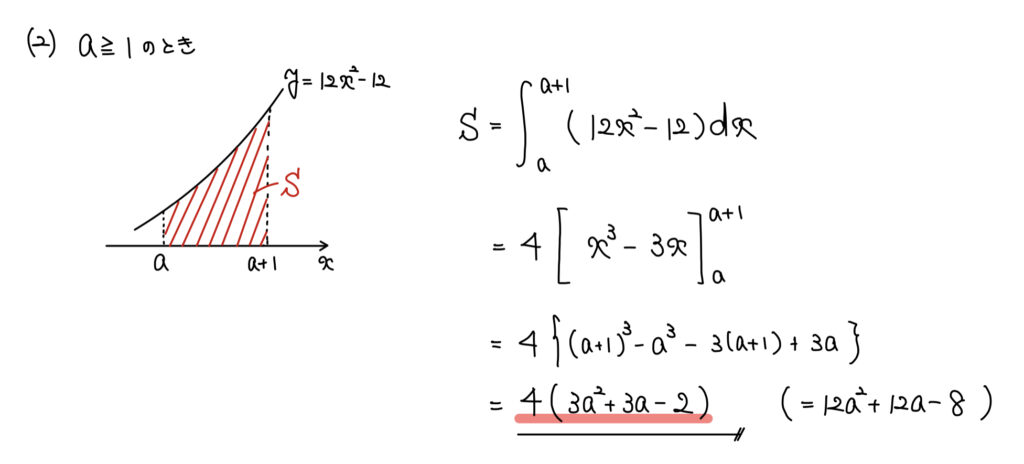
解説
1<aによる面積がどこのことを指しているのかグラフで確認しよう。
その後しっかりと積分計算をしていけば良い。
計算ミスはないように気を付けよう。
(3)2次関数で囲まれた面積、3次関数の最大・最小
解答
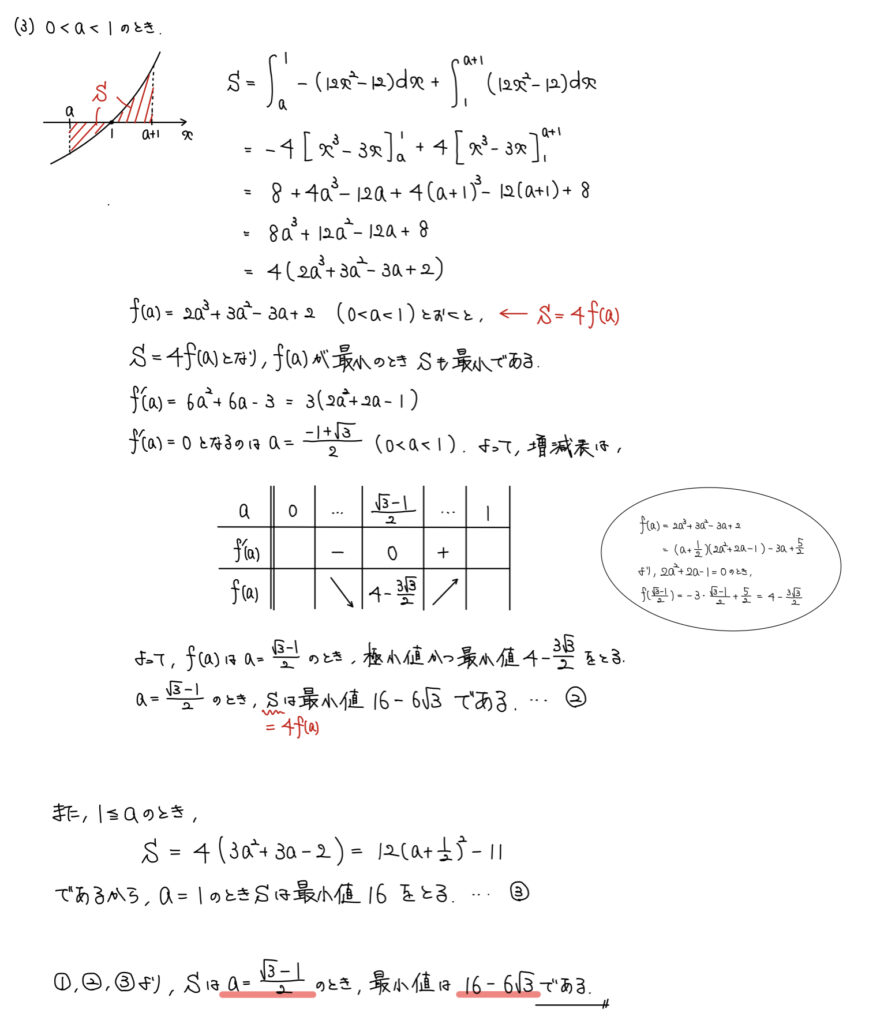
解説
(1)、(2)でa=0、1≦aは確認済みなので、まだ確認していない0<a<1の区間の面積を求めにいこう。
全ての場合漏れなく面積を求めたら、その中で最小なものがこの問題の解答となる。
ということで、0<a<1の区間の面積を求める。
面積の求め方は(1)、(2)と同様なので割愛。
面積がaの式で求めることができたら、あとは求めたaの式の最大・最小問題へと話は変わる。
3次関数の最大・最小問題は微分して増減表で処理しよう。
最後に(1)、(2)、(3)で求めた面積のなかで最小の瞬間に一番小さいものを解答にしよう。
さいごに
単元としては対策をしている人も多いところだろう。
やる処理としてもそんなに難解な処理はなく、標準的。
とはいえ、気を抜くと間違えたり、面積の最小から関数の最小へと話を言い換えることが苦手だと頭がこんがらがってしまう恐れがある。
全体を把握することも重要だが、単元が変わるところでは自分の中で区切っていくなどして何をしているのか見失わない必要がありそうだ。
どういった形でも良いが、自分が何をしているのか、何をしたいのか見失わないようにしよう。
こういった単元を変えながら進んでいく問題は個人的に大好きだ。
楽しい問題だった。
これからも一緒に頑張っていこう。



コメント