2020年度弘前大学の過去問を解いたので解答・解説をしていく。
今回は理工学部数物科学科数学選択者のみが解く問題を解いた。(理系の共通問題ではないので注意)
理系の共通問題は『137話 2020 弘前大学 過去問振り返り』の記事にまとめてあるため、そちらを参考にしてください。
それでは、早速見ていこう。
問題(大問5)
目安時間:45分
2020年度 弘前大学 前期日程 理学部 数学
[ https://nyushi.hirosaki-u.ac.jp/wp-content/uploads/2020/05/R2ze-su3.pdf ]
※上記URL:国立大学法人弘前大学HP 『過去の入試問題』ページより 令和2年度 前期 数学③ⅢB
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。
参考URL『国立大学法人弘前大学HP-過去問題-』https://nyushi.hirosaki-u.ac.jp/faculty/previous-exams/
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
弘前大学は偏差値45.0〜52.5の国立大学(2021年8月1日時点 パスナビ調べ)。
大問5は関数の最大・最小と曲線の長さの問題だ。
関数の最大・最小は数Ⅲあるある処理なのでしっかり得点したい。
正答率も高いことが予想される。
一方,(2)の曲線の長さは対策をしていなかった人も少なくないだろう。
重要な考え方ではあるが、頻出でないテーマではあり(1)が正答でなかった人はまずそちらから学習すべきだ。
とはいえ、出題される以上は対策をしておく必要があるため、余裕がある人や本学科志願者はしっかり復習をしよう。
(1)関数の最大・最小
解答

解説
関数の最大・最小問題はやることが決まっていて、
やることは決まっていて、
- 微分して
- f’(x)=0となるxの値を求めて
- 増減表かいて
- (左方・右方極限を調べて)
- グラフイメージして
- 最大・最小を求める
という手順だ。
計算が少し大変だが、やることが決まっている以上は手を動かせば解答作成ができる。
計算ミスだけないように注意しよう。
(2)曲線の長さ
解答
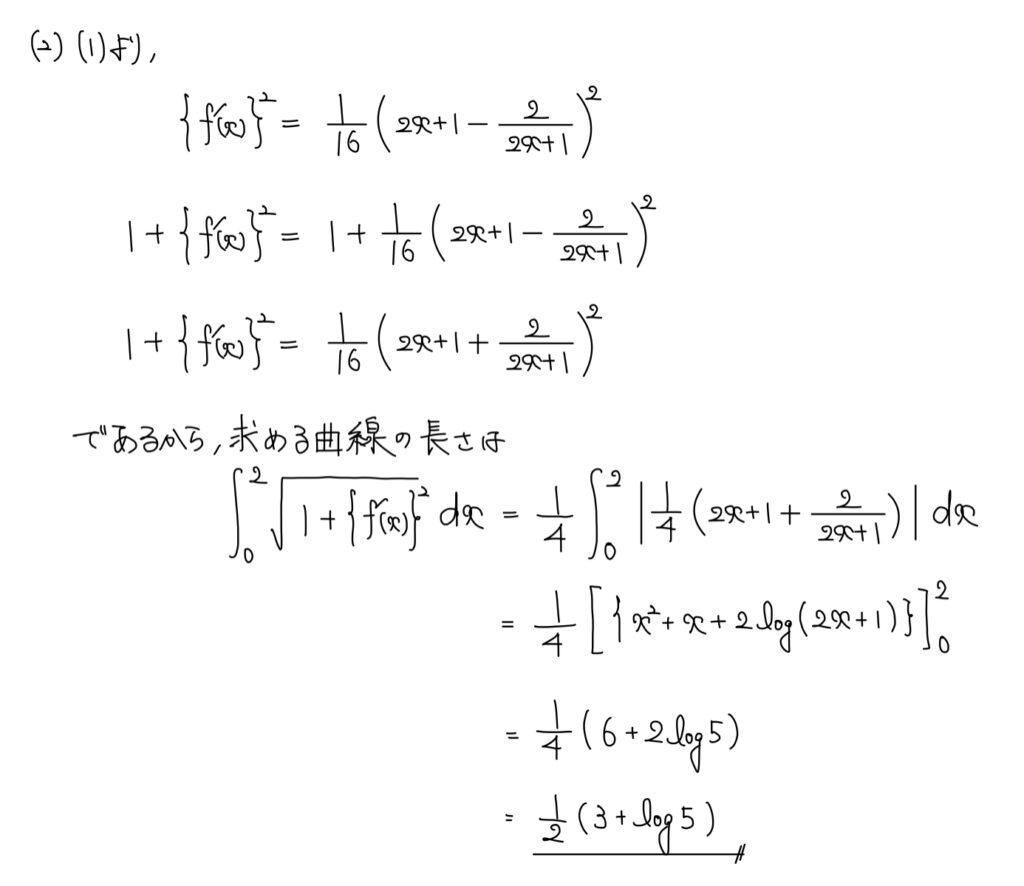
解説
曲線の長さは公式を知っているかどうかが大きい。
公式もただ暗記するのは大変で忘れる恐れがあるため、証明できるまで言わないにしても、なぜ式になるのかは理解しておくと良い。
一気に公式代入が怖い時は解答のように計算過程を追っていくのがオススメ。
解ける人は周りと差がつけられるであろう問題のため、確実に正解できるように気を付けよう。
さいごに
公式の模範解答はこちら
https://nyushi.hirosaki-u.ac.jp/wp-content/uploads/2020/05/R2ze-su3_kaitou.pdf
参考URL:国立大学法人弘前大学HP 『過去の入試問題』ページより令和2年度 前期 数学③ⅢB 解答例
やはり難易度という意味では理系共通問題より難しい。
自分が受験生の時を考えると(2)の曲線は解けなかったと思う。
ちなみに、大学3、4年次に受講する「微分幾何学」においてはこういった曲線の長さなどを扱うことになる。
そんなことを思い出しながら解いてしまった。
懐かしくて楽しい問題だった。
やっぱり数学は楽しいなぁ。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント