2020年度秋田大学の過去問を解いたので解答・解説をしていく。
今回は前期日程の問題を解いた。
大問自体は全学部9題ある用紙を配布されるが、そのうちどの大問を選択して解答するかは学部学科によって異なるため注意して欲しい。
学部ごとにどの大問を選択すれば良いかは以下画像の赤枠内参照。

それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『秋田大学 過去問』で検索してみて欲しい。
目安時間:18分
2020年度 秋田大学 前期日程 数学
[ https://www.akita-u.ac.jp/honbu/exam/pdf/r2_zenki/r2zenki_05.pdf ]
※上記URL:国立大学法人秋田大学HPホーム > 入試情報 > 過去問題 > 令和2年度 > 前期日程 > 数学
※過去8年分が公式HP(下記URL)から閲覧できます。(2021年8月18日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人秋田大学HP>入試情報>過去問題』
https://www.akita-u.ac.jp/honbu/exam/ex_pastissues.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
秋田大学は偏差値42.5〜62.5の国立大学(2021年8月18日時点 パスナビ調べ)。
大問2は循環小数とn進数の問題だ。
難易度としては(1),(2)が日東駒専以下の難易度、(3),(4)が日東駒専以上GMARCH以下のレベルだろうか。
処理が分かっていれば計算や途中式にも時間がかからないため、時間の心配はそんなに気にしなくて良いだろう。
問題の絶対的な難易度は決して高くないが、「n進数」という単元がそもそも対策不足な人が多そうな単元であるため、相対的な難易度としては(4)は結構高いかもしれない。
n進数の学習優先度が低いのは確かだが、こうして出題されることもあるため、今回の問題で復習と演習としてもらえたら嬉しい。
それでは解答を見ていこう。
(1)循環小数
解答
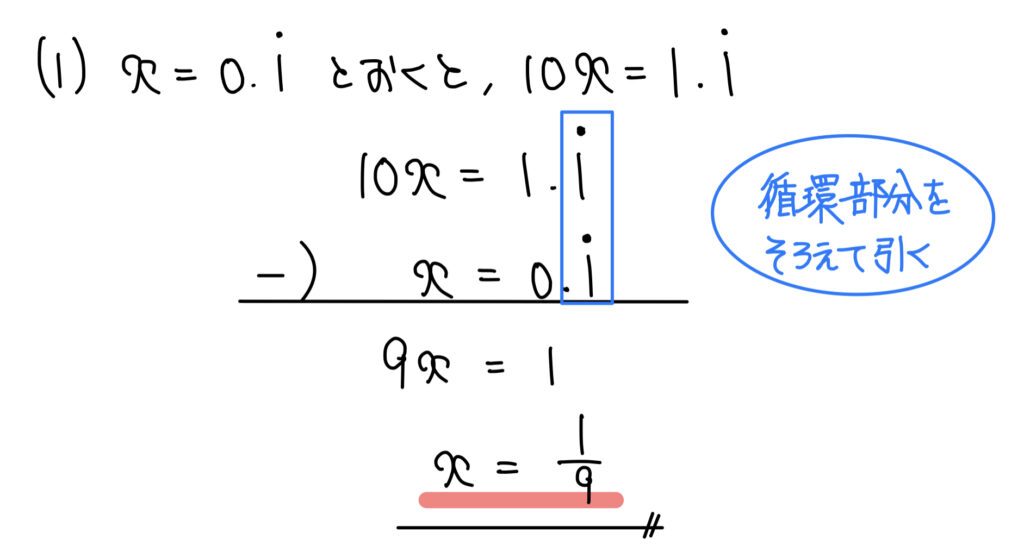
解説
循環小数から分数への変換のポイントは循環部分をそろえて引くことだ。
こうして厄介な循環部分が消えるため分数として表せる。
有理数の問題でたまにある処理のためしっかり押さえておこう。
(2)循環小数
解答
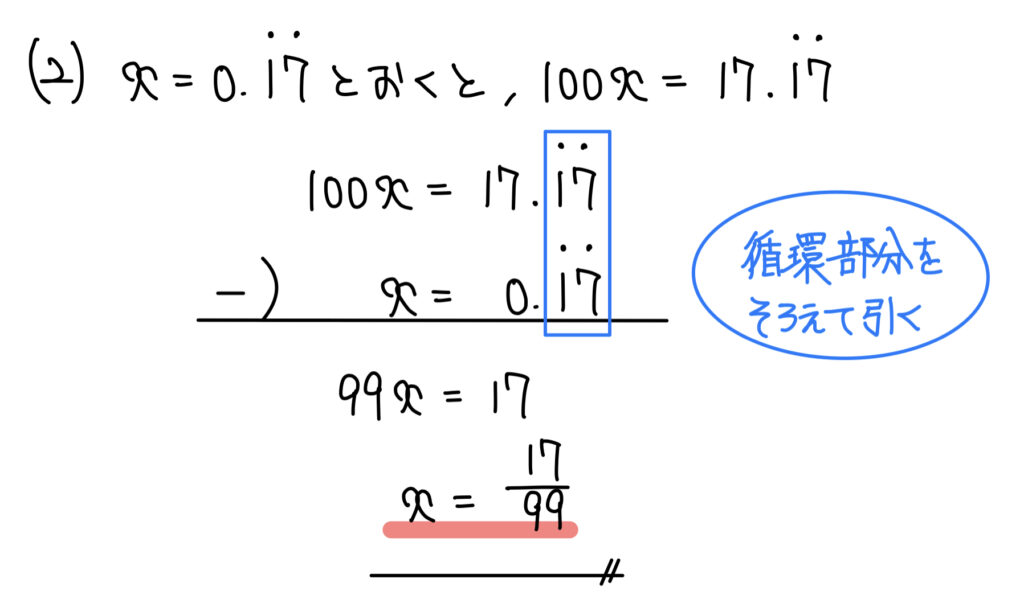
解説
(1)同様、循環部分をそろえて引くことだけ意識しよう。
(3)基数変換(10進数から3進数へ)
解答

解説
「○進数」の○の部分を基数といい、基本的には身近な10進数を中心に考えることが多い。
今回も数字が10進数で与えられているため、基本的な問題と言える。
基数の変換方法はやり方が決まっているため、しっかり押さえておこう。
具体的には次の通り。

今回も例に漏れず、まずは整数部分と少数部分に分けて考える。
そうなった時に厄介なのが循環小数の循環部分だが、これは既約分数へ変換することで解消される。
これは(1),(2)までの流れからも察することができるだろう。
既約分数で表すと少数部分は1×3-1の形を得ることが出来て、解答を得る。
n進法の各位の考え方も一応ここで確認しておく。

(4)基数変換(10進数から2進数へ)
解答

解説
(4)も基数変換であるため、手順は(3)同様。
手順の中で循環部分が出てきたら循環小数である。
さいごに
自分自身n進数の勉強は大学のプログラミングの授業で学習した程度だったが、求められていることは特に変わらず対応できた。
今後は中学生、高校生のうちからこういった問題に多く触れることになるのだろう。
プログラミング関係に関連する可能性がある人はしっかり出来ておくと今後のためにもなりそうだ。
ただ…個人的にはあまり魅力を感じない単元のため、また他の問題にも多く触れていきたい。
面白いn進数の問題にも出会ってみたい。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント