154話 2020 秋田大学過去問大問4【解答解説】

2020年度秋田大学の過去問を解いたので解答・解説をしていく。

今回は前期日程の問題を解いた。

大問自体は全学部9題ある用紙を配布されるが、そのうちどの大問を選択して解答するかは学部学科によって異なるため注意して欲しい。

学部ごとにどの大問を選択すれば良いかは以下画像の赤枠内参照。

それでは、早速見ていこう。

問題

以下のURLは大学の公式HPから入試問題へのリンク。

問題はそちらから確認して欲しい。

URLからのリンクが怖い方は『秋田大学　過去問』で検索してみて欲しい。

目安時間：18分

2020年度秋田大学前期日程数学
[ https://www.akita-u.ac.jp/honbu/exam/pdf/r2_zenki/r2zenki_05.pdf ]
※上記URL：国立大学法人秋田大学HPホーム > 入試情報 > 過去問題 > 令和2年度 > 前期日程 > 数学
※過去8年分が公式HP(下記URL)から閲覧できます。（2021年8月18日時点）
※掲載終了している可能性もあります。
参考URL『国立大学法人秋田大学HP>入試情報>過去問題』
https://www.akita-u.ac.jp/honbu/exam/ex_pastissues.html

まず、実際に解いてみて欲しい。

頑張って。

解けたでしょうか？

それでは解答解説をしていこう。

問題

解答・解説
さいごに

解答・解説

概評

秋田大学は偏差値42.5〜62.5の国立大学（2021年8月18日時点パスナビ調べ）。

大問3は平面ベクトルの問題だ。

難易度としては日東駒専（偏差値45〜55）レベルだろうか。

出題のされ方としても奇抜なことはなく、解答の方針が分かりやすい問題だ。

今回の問題で全然解答の方針が見えなかったという人は、該当範囲をもう一度教科書や基礎的な問題集で復習するのがいいだろう。

それでは解答を見ていこう。

（1）ベクトルの等式

解答

解説

まず、「2つのベクトルが等しい」ことの定義を確認しよう。

「2つのベクトルが等しい」というのは「2つのベクトルの向きと大きさが等しい」ことをいう。

これを成分で言うと「各成分が等しい」ということになる。

この上で解答の方針に至るまでの思考過程は以下の通りだ。

ベクトルが成分で与えられている　→　成分で解答を作るのかな
2つのベクトルが等しい条件　→　それぞれ成分で表して各成分が等しい

方針が決まったらあとはその通り（解答の通り）手を動かしていけば良い。

（2）ベクトルの平行、ベクトルの内積

解答

解説

初見で見た時の方針決めまでの思考過程は次の通りだ。

与えられた条件は①垂直と②平行の2つ
①垂直（角度）が与えられたら「（内積）＝0」の利用
②平行な2つのベクトルは実数(k)倍で表せる
①、②でそれぞれ式が出てきて連立するんだろう

この問題を解き終わったからこのような手順解説ができるわけではなく、この問題を見た瞬間にこの方針は見えてくる。

経験値といえばそうだが、「角度が与えられたら内積処理」や「平行は実数倍」というのは基本事項なので、その方針が全然見えなかった人は過去問演習の前に基本事項の確認をすることを勧めたい。

どちらも様々な問題に出てくる条件なのでしっかり押さえていこう。

（3）ベクトルの内積

解答

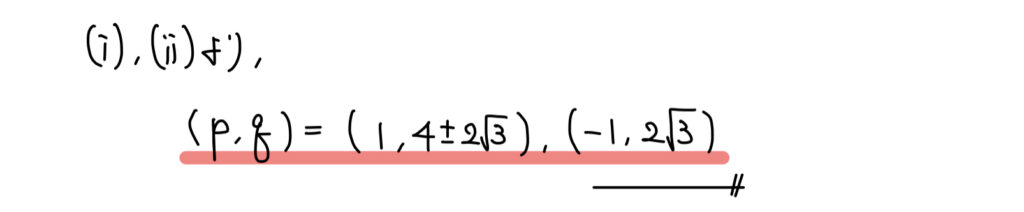
解説

初見での解答の方針決めは次の通り。

①大きさと②角度についての情報が与えられた
①成分が与えられているから、大きさを成分から立式して処理
②角度の情報が与えられたら内積
角度の内積からどうやって方程式を導こうかな
成分での内積と角度での内積で立式すればいいか

ここからは方針の中身を見ていこう。

まず、内積問題は次の4つのアプローチを必ず頭に入れておこう。

大きさとなす角
成分（同一成分の積の和）
大きさの2乗
正射影

内積は上記の考え方以外で出現しない。

ゆえに、この4タイプのみで内積のアンテナを張ればいい。

内積の出題パターンが上記の4通りと知った読者の皆さんは、今後「内積を使う問題と気付けなかった」ということが起こり得なくなった（はずだ）。

逆に、上記の条件が与えられた瞬間に内積を疑おうであることに気付こう。

ただ、「正射影」という言葉を聞いたことがない人もいるかもしれない。

正射影は難関大学では当たり前のように扱う内積問題のアプローチの1つなのだが、申し訳ないがここでは詳細は割愛させてもらう。

気になる人は「ベクトル　正射影」で検索してみて欲しい。

難易度は上がってしまうが『27話　ベクトル道場2　〜2020 一橋大学(前期) 大問3〜』でも解説はしている。

話を今回の問題の解法に戻す。

4手順目のベクトルの内積において、成分表示に気付けないで間違えてしまった人は、解答を見て（あ、成分表示でも表されるんだ！なるほどね！）となったかもしれない。

しかし、そもそもベクトルが得意な人はそういう思考ではない。

ベクトルが得意な人は、成分が与えられている時点で解く前から（あ、大きさも内積も求められるじゃん）ということが分かっている。

そこに角度の情報が問題文で与えられたため、（あ、角度でも内積表せるのね）という思考になるのだ。

それほど成分（座標）の情報というのはベクトルにおいて存在が大きい。

ただ単に成分の加法減法、実数倍ができるだけではなく、与えられた時点で大きさと内積が分かる超強力武器であるということをしっかり把握しておこう。

そうでないとまた類似問題で（あ、この問題どうすればいいんだっけ？）と発想勝負みたいになってしまう。

また、ベクトルの話とは少し変わってしまうが、平方根の計算において両辺2乗するときは解答のような注意が必要であることは知っておこう。

これはきっと大勢がミスをする部分であるから、ミスをしなかった自分だけがかなり得することができるチャンスだ。

そもそも、数学において答えが2つ出てきたら両方正しいのかどうかは疑おう。

「2次方程式は解2つに決まってる」ではなくて、「問題文の条件を全て満たしているのか」という視点で疑うことで間違えずに済む。

たったそれだけの注意で周りと差がつくため、まずは意識してやってみて欲しい。

さいごに

自分はベクトル分野は得意なため、個人的には物足りない問題だった。

とはいえ、こうして改めて文章にするとしっかり解答の方針が見えていることが確認できるので自分にとっても良い。

ベクトルは慣れてくるとかなり方針決めが簡単な単元であり、かつ、数学ⅠAの図形問題も解けてしまうため強力な武器になる。

少しずつでいい。

方針が見えてくるよう学習を進めていこう。

解いた方お疲れ様でした。

これからも一緒に頑張っていこう。

その他過去問を解く人はこちらから　→　『特集　過去問振り返りまとめ』

本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。
尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。
コメントいただければ確認、修正致します。
何卒よろしくお願い致します。