2020年度秋田大学の過去問を解いたので解答・解説をしていく。
今回は前期日程の問題を解いた。
大問自体は全学部9題ある用紙を配布されるが、そのうちどの大問を選択して解答するかは学部学科によって異なるため注意して欲しい。
学部ごとにどの大問を選択すれば良いかは以下画像の赤枠内参照。

それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『秋田大学 過去問』で検索してみて欲しい。
目安時間:22分
2020年度 秋田大学 前期日程 数学
[ https://www.akita-u.ac.jp/honbu/exam/pdf/r2_zenki/r2zenki_05.pdf ]
※上記URL:国立大学法人秋田大学HPホーム > 入試情報 > 過去問題 > 令和2年度 > 前期日程 > 数学
※過去8年分が公式HP(下記URL)から閲覧できます。(2021年8月18日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人秋田大学HP>入試情報>過去問題』
https://www.akita-u.ac.jp/honbu/exam/ex_pastissues.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
秋田大学は偏差値42.5〜62.5の国立大学(2021年8月18日時点 パスナビ調べ)。
大問5は三角関数と不等式の問題だ。
難易度としてはGMARCHレベルだろうか。
(1),(2)については方針決めとその計算が分かりやすいように思う。
(3)は「すべてのxに対して」というよくある問題文ではあるのだが、方針決めや同値性といった部分で言えば多くの受験生があまり得意でない分野なのではないだろうか。
日頃から同値性について意識しながら解答を書いているという人はあまり多くないのではないだろうか。
「必要十分条件を調べよ」と言われたら調べられると思うが、命題の理解があまり他単元に活かせていない人も多いように思う。
そういった方にとっては非常に有効な問題で、かつ、方針さえ決まればやることは難しくない良い問題だ。
完答という基準で言えば(3)が一番難しいように思う。(必要、十分条件のどちらかだけ示している人は多くいると思う)
(4)は解の個数問題で問題集にもありそうな問題だ。
解答している途中で自分が何を示したくて書いているのか見失わないように気を付けよう。
それでは解答を見ていこう。
(1)三角関数を含む方程式・不等式
解答

解説
不等式といえば「大ー小の形を作る」!と覚えている人は多いだろう。
今回も実際それで良い。
方針さえ決まればあとは解答の通り。
cos(π-x)はすぐに-cos(x)に直して考えよう。
(2)三角関数を含む不等式
解答
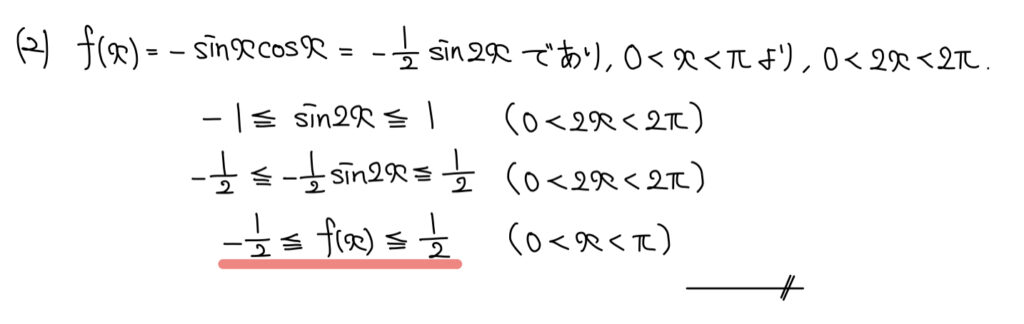

解説
三角関数で不等式といえば必ず意識したいのが三角関数は−1以上1以下ということだ。
使うか使わないかは不明でも、この条件は(使えないかな?)と常に念頭に置いていおこう。
f(x)を見ると、sinとcosという変数が2つあるため考えづらい。
2つの変数を1つにできないかな、という目線で見るとsinの倍角の公式が見えてくるのでは無いだろうか。
倍角の公式まで辿り着いたらあとは1つの変数なので「三角関数は−1以上1以下」で解答の通り。
別解について。
三角関数においては和(sin+cos)と積(sin×cos)が1変数tで表せるという特徴がある。
ゆえに、和や積を含む問題ではt=sin+cosとおくことが非常に有効であり、こういった問題を解いたことがあるのでは無いだろうか。
三角関数において和をtで表せたと言うことは積をtで表せることでもあり、tの整関数(xnの形の関数)で表すことができる。
整関数にさえなってしまえば範囲、すなわち、最大・最小を求めるの簡単で、2次関数なら平方完成、高次関数なら微分して増減表だ。
圧倒的に別解では無い方が速いためそちらを推奨するが、三角関数で和や積が見えたらt=sin+cosの置換が有効ということは知っておこう。
(3)命題、三角関数を含む方程式・不等式
解答

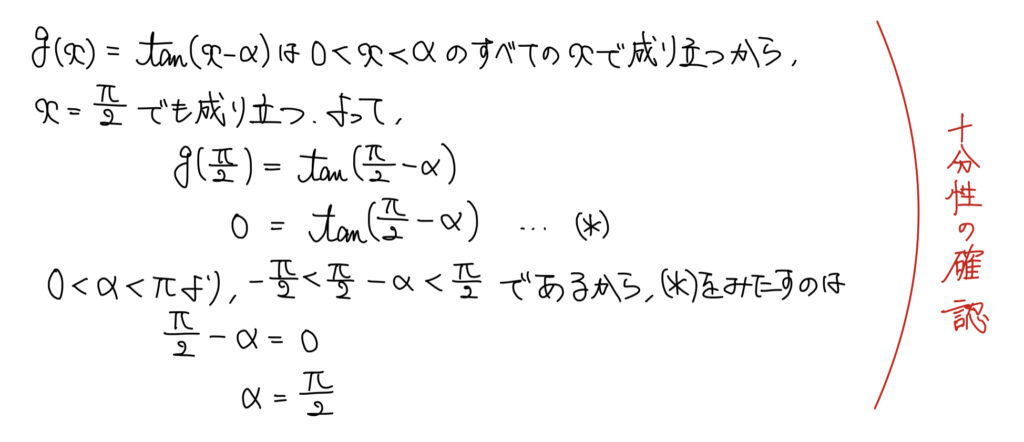
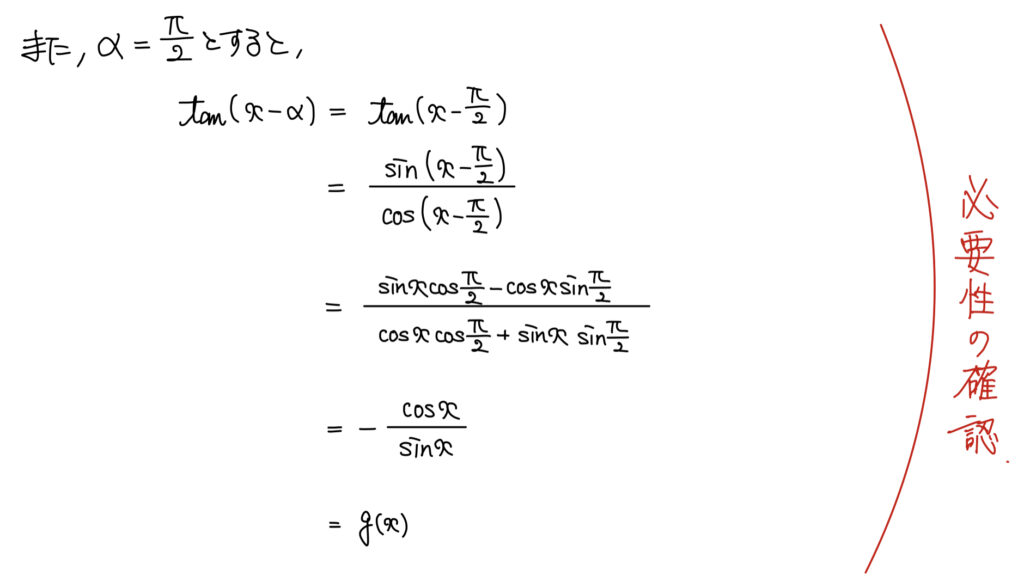
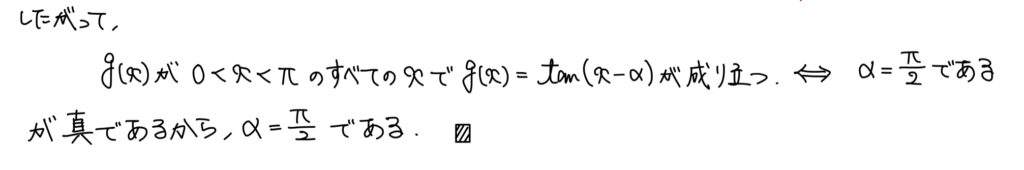
解説
解答の方針は解答最上部赤文字のところに書いた通り。
これは自分がこの問題を解いた時の思考を文字化したものだ。
この問題はこの発想ができたかどうかが鍵だ。
方針さえ決まってしまえばやることは簡単だ。
十分性の方は特に言うことはなく解答の通り。
必要性について(この式変形が見えていなかった)という人もいるかも知れないが、これは実はメタ的な考え方で解決できる。
十分性の確認でαが1つしかなかったため、おそらくこれが答えなのだろうと思いながら計算をしている部分は少しある。
ゆえに(あとはg(x)に変換するためにsinとcosが出てくる式を作りたい)と思い、tanからsinとcosが出てくる式と言ったら流石に三角比の相互関係が思い付くのでは無いだろうか。
(4)解の個数、三角関数
解答

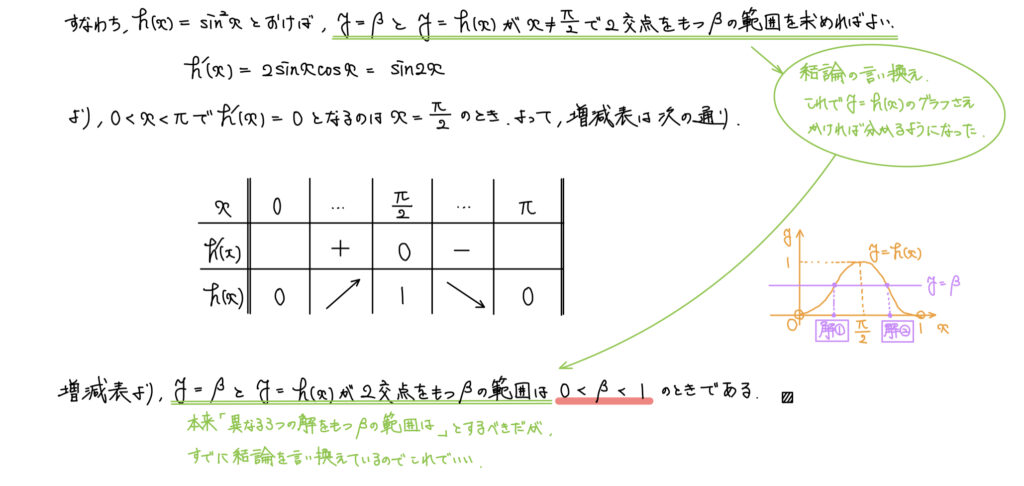
解説
解の個数や範囲についての問題ではグラフ処理が有効に働く。
そして、このような問題で多いのが今回でいうβのような定数が与えられるパターンだ。
この時の基本方針は次の2つだ。
- 定数分離(「β=」の形を作る)
- 0分離(「0=」の形を作る)←定数分離が難しいとき
今回は定数分離ができるパターンのため、「β=」の形を作る。
この時点で「グラフ処理をするから定数分離をした」と意識的に定数分離をしていれば、迷わずグラフを描くことになるだろう。
解答はグラフを描くために微分して増減表とセオリー通りに書いたが、正直y=sin2xくらいなら増減表は不要だとも思っている。
ザッとかいてグラフより、で良いと思う。
また、示すべきことの言い換えをする場合は、誰がどう見ても(あ、そっちを示すことで題意を示すのね)と分かるようにしよう。
そうでなければ勝手に関係ない証明を始めた人になってしまう。
個人的には「〇〇を示すためには△△を示せばよい」という書き方をオススメする。
そうすれば〇〇と△△が同値であることは読み手の誰もが分かる。(本当に同値な主張かどうかはしっかり確認すること)
最後に、最初の式変形の発想がなかったという人用に一言言っておくと、方程式を解く時に「●=0」の形を作って因数分解はまず考えることだ。
出題のされ方で基本事項を見失わないように注意しよう。
さいごに
今回の問題は個人的にはとても好きな問題だった。
特に(3)は命題の重要性が詰まっていてとても良い。
受験生で同値性を正しく使いこなせるのは結構な上位層であるように思う。
自分も完全に理解しているとは言えないが、それでもある程度同値性を理解しただけでも、軌跡・領域をはじめ全ての単元での問題文の見方が変わってくる。
この1問を最初の土台として、これから同値性について少しずつ目を向けていけるようになっていきたい。
解いた方、お疲れ様でした。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント