2020年度秋田大学の過去問を解いたので解答・解説をしていく。
今回は前期日程の問題を解いた。
大問自体は全学部9題ある用紙を配布されるが、そのうちどの大問を選択して解答するかは学部学科によって異なるため注意して欲しい。
学部ごとにどの大問を選択すれば良いかは以下画像の赤枠内参照。

それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『秋田大学 過去問』で検索してみて欲しい。
目安時間:20分(医学部は18分)
2020年度 秋田大学 前期日程 数学
[ https://www.akita-u.ac.jp/honbu/exam/pdf/r2_zenki/r2zenki_05.pdf ]
※上記URL:国立大学法人秋田大学HPホーム > 入試情報 > 過去問題 > 令和2年度 > 前期日程 > 数学
※過去8年分が公式HP(下記URL)から閲覧できます。(2021年8月18日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人秋田大学HP>入試情報>過去問題』
https://www.akita-u.ac.jp/honbu/exam/ex_pastissues.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
秋田大学は偏差値42.5〜62.5の国立大学(2021年8月18日時点 パスナビ調べ)。
大問6は積分方程式についての問題だ。
難易度としてはGMARCHレベルだろうか。
積分方程式は数学Ⅲの最後の方に学ぶ内容でもあり、苦手というより理解があまりできていない人が多いような単元でもある。
今回の積分方程式の問題はかなり基礎的な内容でありながら、積分方程式の様々なパターンに触れている良問題だ。
世に良問として言われるものではないかもしれないが、積分方程式についての基本的な理解を問うという点に関して、個人的には非常に良問だと思う。
医学部志望の人もこの問題は解いているわけだが、その人たちは18分程度を解答の目安時間にしたほうがいいだろう。
解答の方針はすぐに見えるため、計算ミスや記述ミスに十分に注意したい。
それでは解答を見ていこう。
(1)積分方程式(区間が定数)
解答

解説
関数が与えられていてその定積分を聞かれているので、問われている通り定積分を計算すればいい。
基本的に区間が定数の定積分は定数扱いするため、関数さえわかれば計算して定数が何か把握しておいた方がいい。
また、解答の積分計算について、対数の積分は頻出のためいちいち部分積分せず覚えてしまうことをオススメしたい。
自分はx・logxや(logx)2の積分を覚えていて、計算の必要がなくなっている。
上記のような積分は頻出のため、受験期間中だけでも覚えてしまった方が便利だ。
覚えた人は今回次のような応用(※の部分)が可能だ。

上の※において、x+a形であれば今回のような応用が効く。
ax,ax+bの形については合成関数の積分のためaで割って上げる必要があることに注意しよう。
(2)積分方程式(区間が定数)
解答
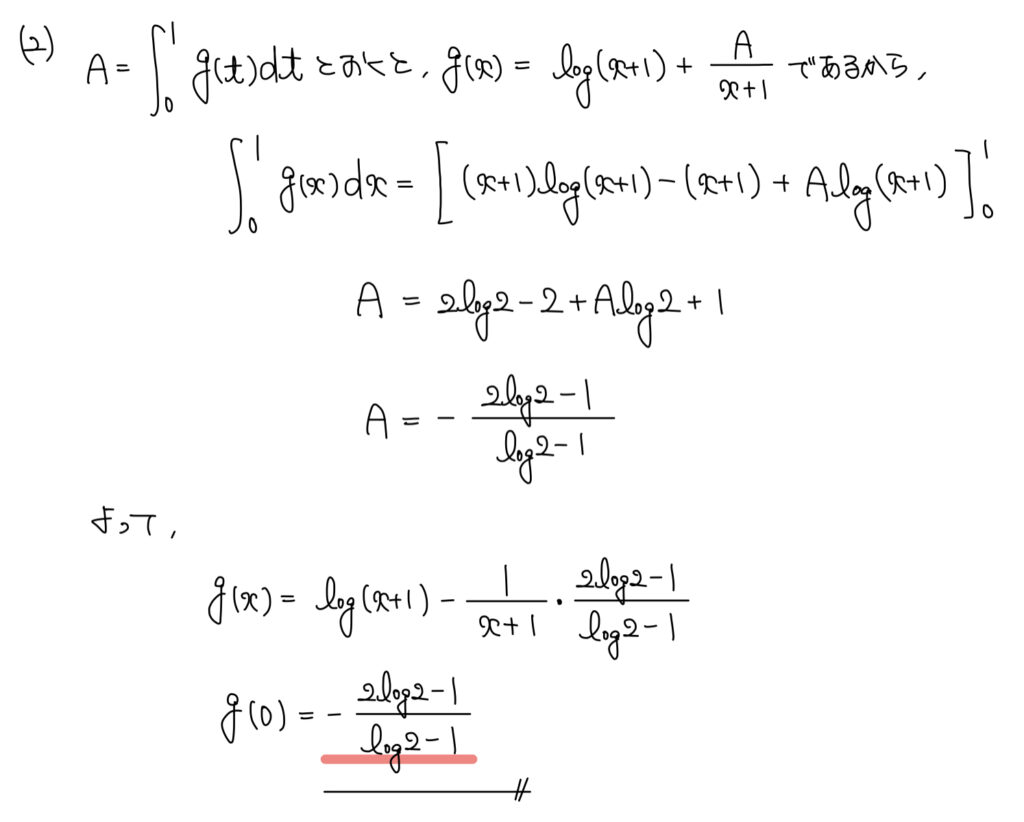
解説
区間が定数の積分は定数扱い。
ゆえに、「A=」という形で定数扱いしよう。
定数であるから積分計算もできて、後は解答の通り。
(3)①積分方程式(区間が変数)
解答
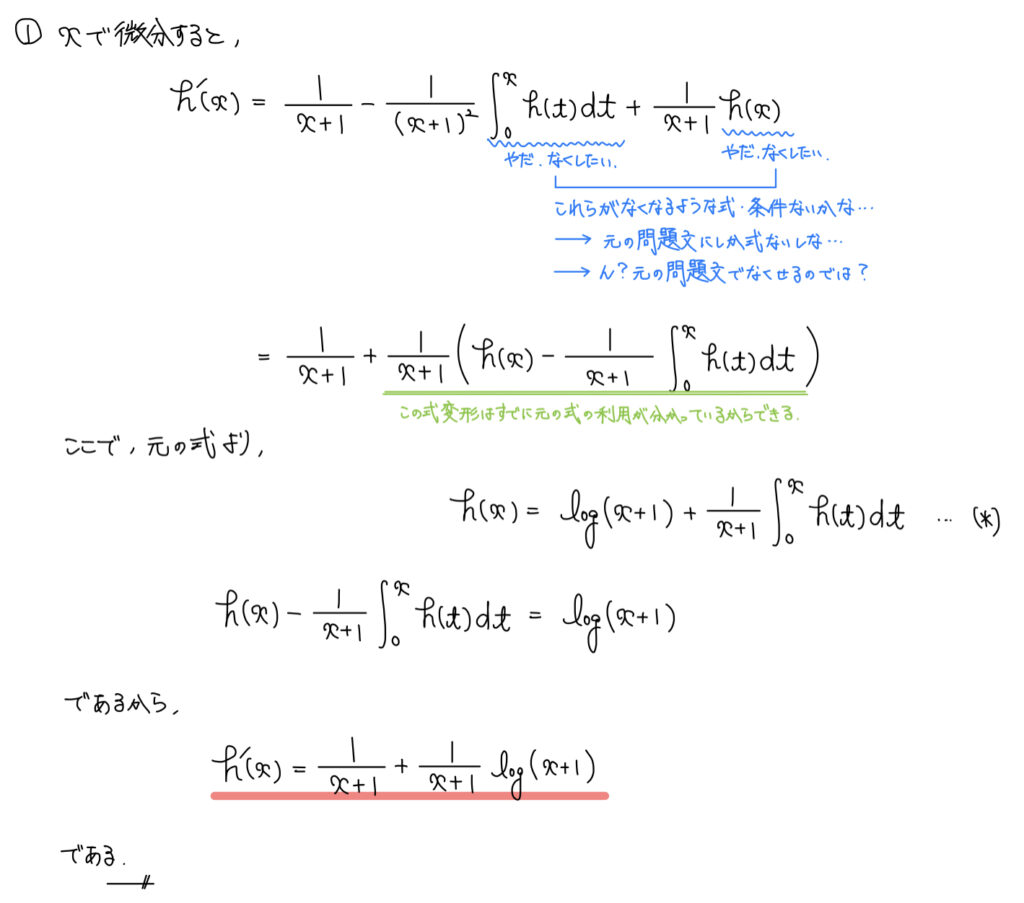
解説
区間が変数の積分方程式については次の方針でいこう。
- 微分して区間代入(上の区間ー下の区間)
- 区間の片方が定数の場合(仮にaとする)は変数にaを代入して「=0」とする → 元の関数が求められる
今回もこの方針なのだが、2番目の定数代入はやらなくていい。
なぜやらなくていいかというと、今回聞かれているのは導関数であり、元の関数について特に必要ないからだ。
この手順を知っている人は微分をしてくれると思うが、そこで(ん?)となる。
微分しても元の関数やインテグラルなどが消えないのだ。
そこで困って挫折…という人もいるかもしれないが、それはもったいない。
基本方針さえ固まっていれば、その先の応用は必ず問題文にある。
ちゃんと解けるように全て準備されているから安心して欲しい。
今回与えられている条件を見ると
- x>-1 ← 真数条件
- h(x)が連続 ← 定積分ができる条件(定積分の定義)
- h(x)の式
の3つしかなく、使えるのが一番下しかないのに気付く。(上の2つがどこから出てきた条件か気付かなくても最も大きい手がかりがh(x)の式であることには気付くのではないだろうか)
後は頼りのh(x)からどうにかして今の状況を解決できないかな…と頭を悩ませれば解答のような発想に至る。
基本方針が見えてこの問題が解けないのはもったいない。
解法の方針が合っているのであれば、自信を持って他からヒントがないか探す癖をつけていこう。
(3)②不定積分と初期条件
解答

解説
①の解答より積分する。
不定積分になるため、積分定数を忘れないように注意しよう。
ただの不定積分ならこれでおしまいなのだが、今回は「h(x)を求めなさい」という問題のため、積分定数Cが何かもちゃんと書かないといけない。
ここで、思い出して欲しいのだが、①の解法の方針で自分は次のように書いた。
- 微分して区間代入(上の区間ー下の区間)
- 区間の片方が定数の場合(仮にaとする)は変数にaを代入して「=0」とする → 元の関数が求められる
そして、①では導関数を導くだけでよいから2番目の手順を省略したが、②ではまさに元の関数を聞いている。
ということでx=0代入で元の関数を求めにいけばいい。
結局は全て手順通りに解法が出るといった問題だった。
さいごに
今回の問題は
- 基本解法の重要性
- 入試問題は問い方を変えて受験生の基礎力を確認している
という2つのことが非常に良く見えるいい問題だった。
これからも基本的な解法や方針決めというのは意識して勉強していった方がいいことを改めて認識させられた。
良い問題だったなぁ。
自分で作問していたら誰かに自慢するような基本よりの応用問題で心地良かった。
解いた方お疲れ様でした。
これからも頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント