2020年度秋田大学の過去問を解いたので解答・解説をしていく。
今回は前期日程の問題を解いた。
大問自体は全学部9題ある用紙を配布されるが、そのうちどの大問を選択して解答するかは学部学科によって異なるため注意して欲しい。
学部ごとにどの大問を選択すれば良いかは以下画像の赤枠内参照。

それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『秋田大学 過去問』で検索してみて欲しい。
目安時間:25分
2020年度 秋田大学 前期日程 数学
[ https://www.akita-u.ac.jp/honbu/exam/pdf/r2_zenki/r2zenki_05.pdf ]
※上記URL:国立大学法人秋田大学HPホーム > 入試情報 > 過去問題 > 令和2年度 > 前期日程 > 数学
※過去8年分が公式HP(下記URL)から閲覧できます。(2021年8月18日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人秋田大学HP>入試情報>過去問題』
https://www.akita-u.ac.jp/honbu/exam/ex_pastissues.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
秋田大学は偏差値42.5〜62.5の国立大学(2021年8月18日時点 パスナビ調べ)。
大問9は循環小数とn進数の問題だ。
難易度としてはGMARCH以上早慶上理レベルだろうか。
受験生の対策が薄くなるこの単元でこの難易度。
(1),(2)は比較的考えやすい問題で解ける人も少なくないだろう。
しかし、(3)を正答できた受験生は相当少ないのではないだろうか。
個人的には全ての大問の中で完答が1番難しい問題のように思う。
逆に言えば、(1),(2),(4)の部分点さえちょこちょこ取れば、(3)ができないという理由でそこまで周りと差がつくことはないだろう。
本大問はn進数(特に小数部分)の考え方について色々なパターンを知ることができるとても良い問題だ。
(3)も初見で解くことこそ難しいと思うが、解答解説を見て復習してもらうと(1),(4)とやりたいことは変わらないことに気付く。
ゆえに、「難易度が高くなってもやりたいことは変わらない。ただし、アプローチの仕方は様々ある」というのを実感させてくれる。
そういった意味で本問題は貴重な問題だと思う。
単元としては出題頻度が低く、大量に時間を割くのが賢明とは言えないが、この問題を通して基礎事項とやりたいことのイメージを掴んでもらえたら嬉しい。
それでは解答を見ていこう。
(1)基数変換(10進数から3進数へ)
解答
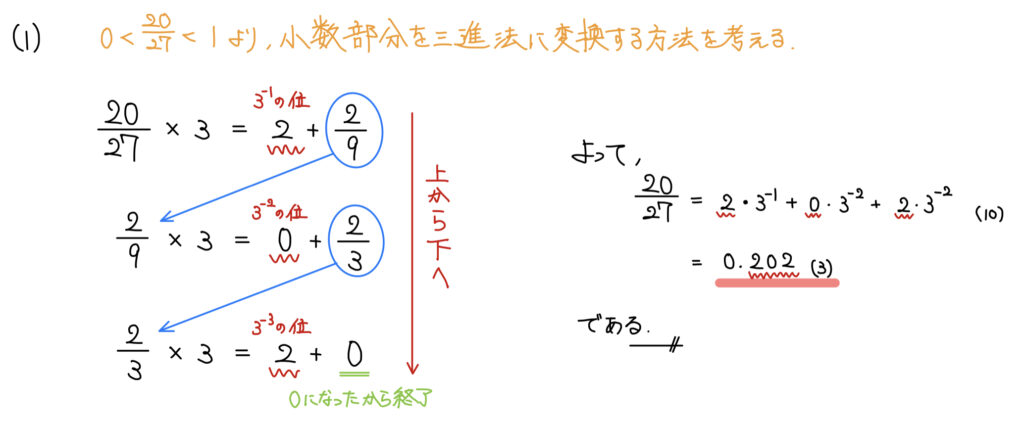
解説
基数変換の方針は次の通りだ。

整数部分と小数部分が混在している場合にはそれぞれ分けて考えるが、今回は20/27が整数部分は0で小数部分のみのため、小数部分のみ考えればいいことが分かる。
今回小数部分の基数変換は整数部分を切り捨てながら小数部分が0になるまで3をかけることを考えればよい。
方針が決まったあとは計算をすればよい。
(2)基数変換(3進数から10進数へ)
解答
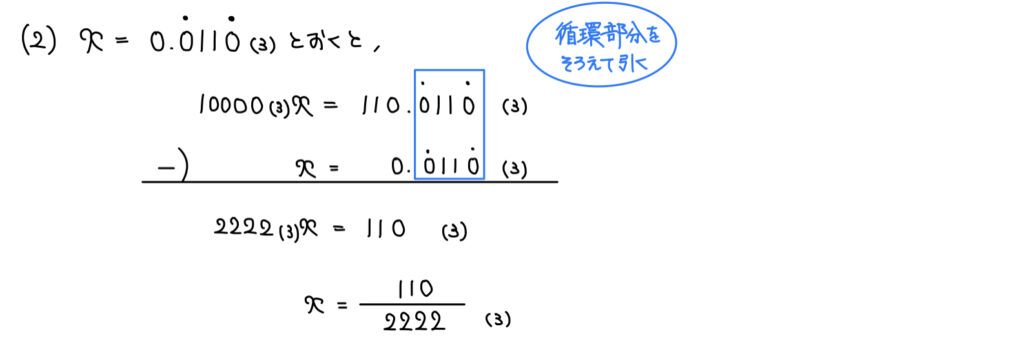
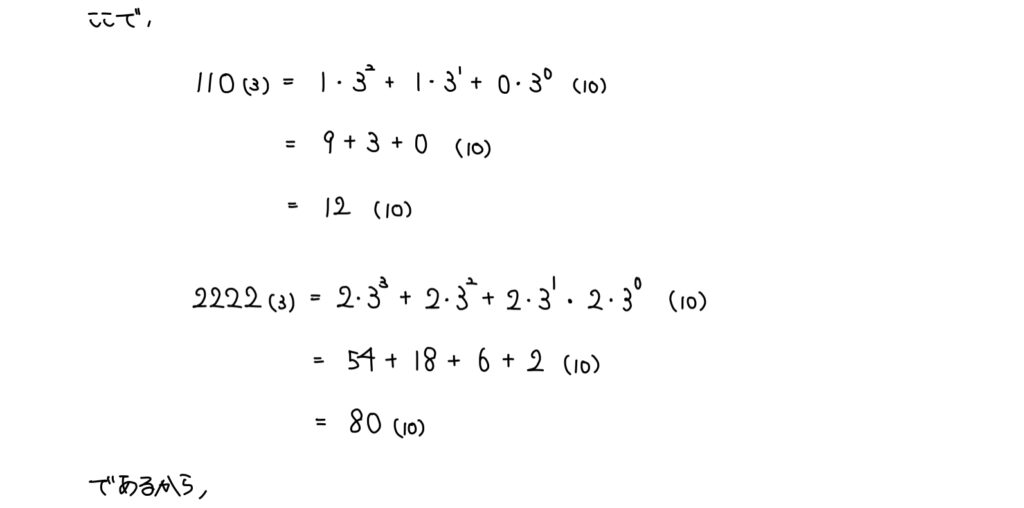

解説
今回厄介なのが「循環小数」である点だ。
まず厄介な循環小数を既約分数の形で表したい。
とは言え10進数以外の循環小数処理を知らないというのが多くの人の反応だろう。
そこで考えるのは知っていること(10進数)と同様に考えるということだ。
10進数の循環小数から既約分数への変換は「循環部分をそろえて引く」という方針で循環部分を処理することができた。
3進数になってもやることは同じだ。
循環小数をそろえて引こう。
既約分数への変換ができたらここからは有限小数の処理であるから各位に注目して10進数へ変換すればいい。
最後は分数の形ではなく組を答えるようにして結論を得よう。
(3)基数変換(10進法から3進法へ)
解答
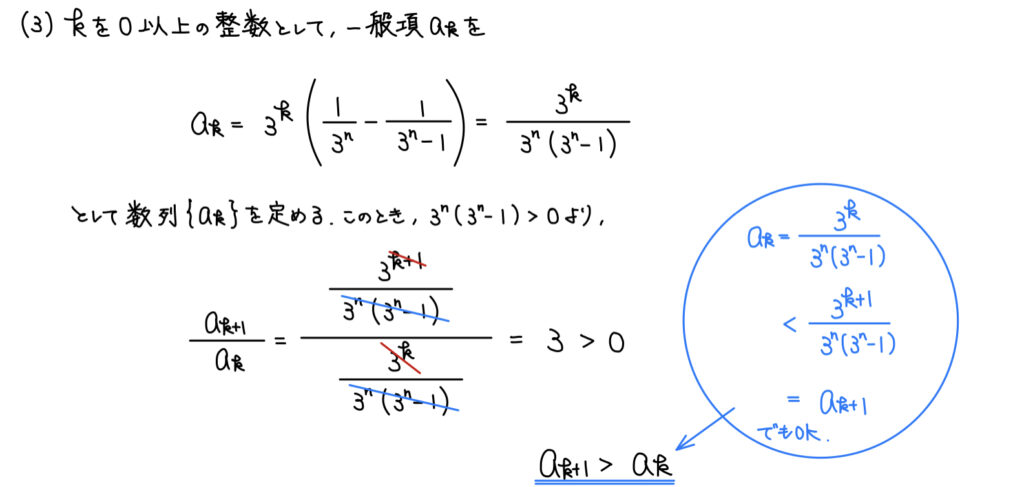
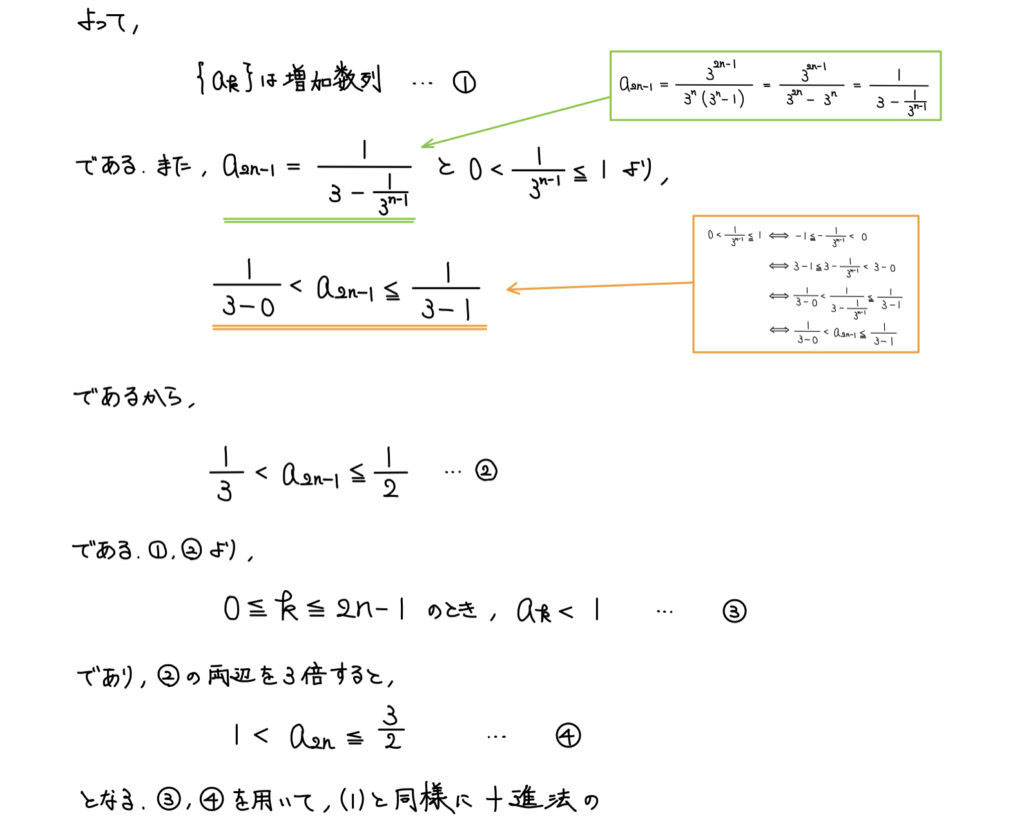

解説
何をやればいいか分からず、まず通分してみたのではないだろうか。
しかし方針が見えず断念、というのが大半の人の解答のように思う。
まず、方針決めの前に小数の10進数から3進数への基数変換の基本解法を確認しておこう。
小数部分においては(1)同様「整数部分を切り捨てながら小数部分が0になるまで3をかける」ということになる。
この際、整数部分で1が現れたらこの問題は終了となる。
つまり、この問題は整数部分として1が現れるまで3を何度もかけ続けるということになる。
ここまでが前提の確認。
さて、方針決めまでの思考の流れを確認しよう。
- 3を何回かけたらいいか分からないから文字でおく(今回はk)
- 3をk回かけたことを想定したい
- k回かけたとして立式(数列の作成)
- そもそも3をかける毎に数字が大きくなってもらわないと整数部分が出てこなくて困る
- 3をかける毎に数字が大きくなることを確認(増加数列)
- 分母に着目し、端数の-1を無視すると32nであることから、おそらく2n回くらいかけたら整数になりそうだな、と予想する
- では、2n-1ではどうなのか試してみる
- どうも2n-1ではまだ整数部分は現れないようだ
- では、さらに3をかけたら(2n回かけたら)?
- 整数部分に1が出てきた(2でないことも合わせて確認)
- 3を2n回かければいいわけだから、小数第2n位で1が初めて現れる
こうした思考の流れで解答が進んでいくわけだが、特に重要なのは太字の箇所だ。
実はこの辺りは推測できそうだ。
推測ができるとあとは論理を構築していけばいいという風になる。
この分からない問題に対しての推測が基本方針を組む上でも重要になってくるため癖をつけておこう。
解答はなるべく一読で分かってもらいたいと思い、不要な途中式なども足してしまっている。
解答用紙に書く際はスッキリするためにも、途中式は自分だけしか見ないスペースで書くようにしたい。
(4)合同式、基数変換(10進数から3進数へ)
解答

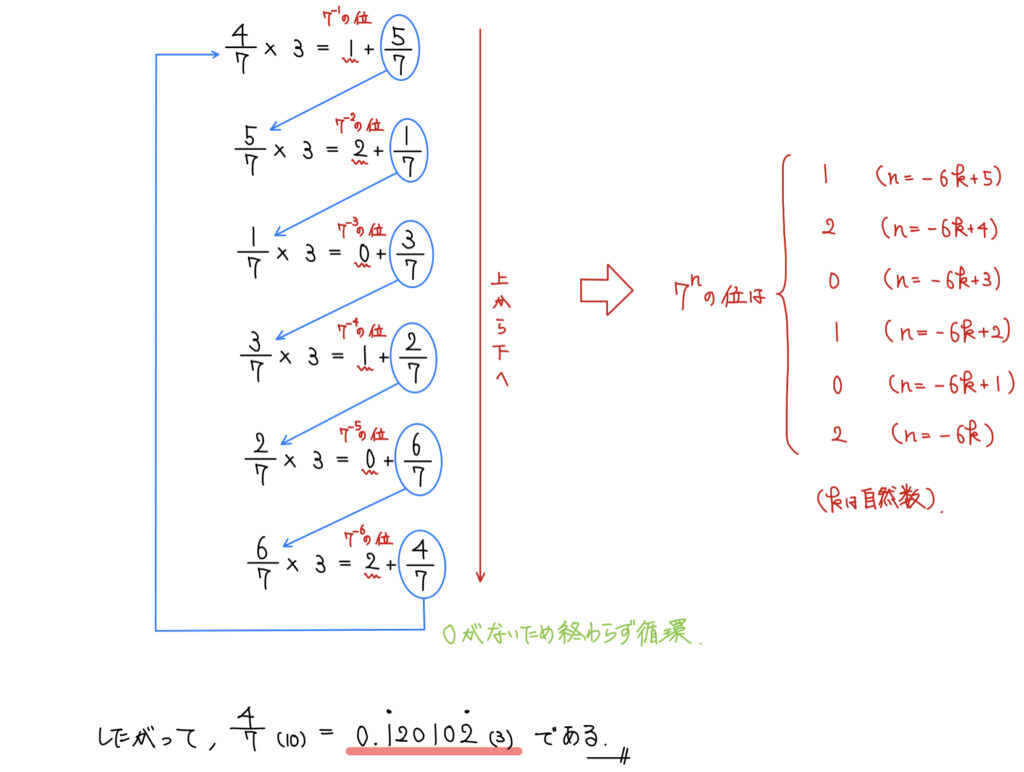
解説
指数型の余りの基本方針は次の通りだ。
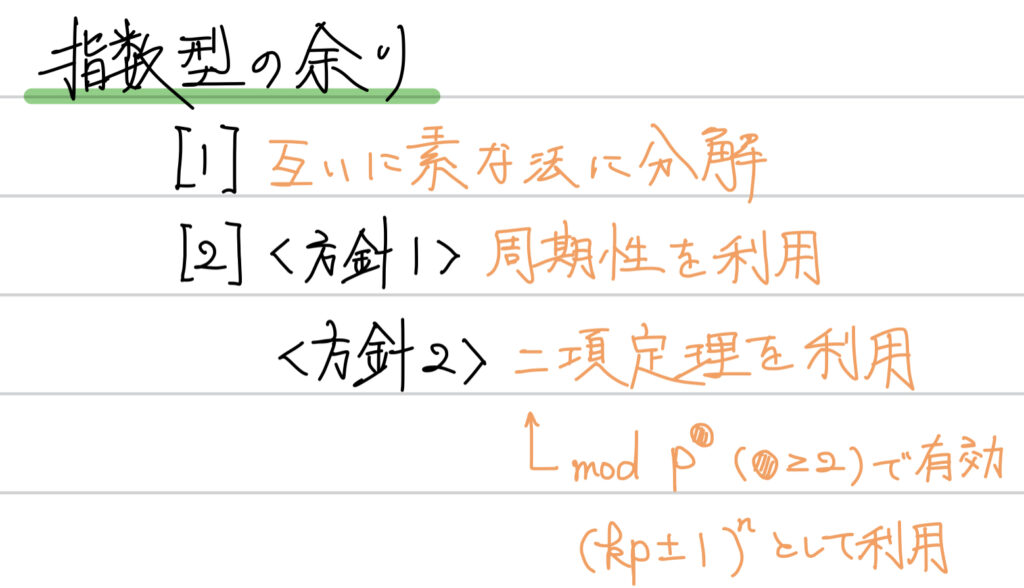
「互いに素な法に分解」とは、例えば割る数が12であったら3と4に分割といった具合に考える。
ただし、今回は割る数が7のため「互いに素な法に分解」する必要はない。
あとは余りの周期性を利用しながら累乗を処理していく。
これが1番速いが、別解では二項定理を用いて解いたため、合同式を知らない人はそちらを確認してもらいたい。(医学部受験生は合同式を知っておくことをオススメする)
余り、すなわち、小数部分が分かったらそこからは(1)と同様。
解答の方針は(1)の解答解説を参考してもらいたい。
(1)と異なるのは循環することだが、それは同じ手順で解いていれば循環に気付く気付くため大きな問題ではない。
この際、循環小数の求め方も知っておこう。
(4)【別解】二項定理を用いた解法
解答

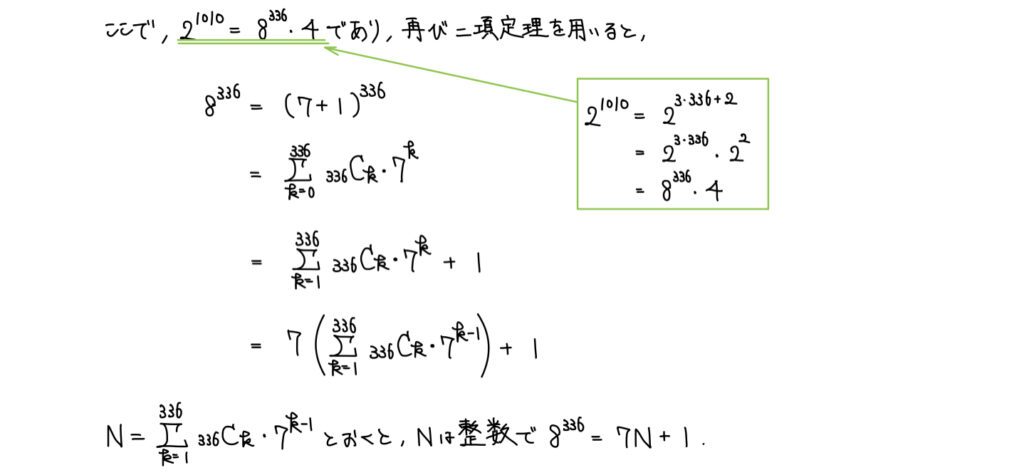
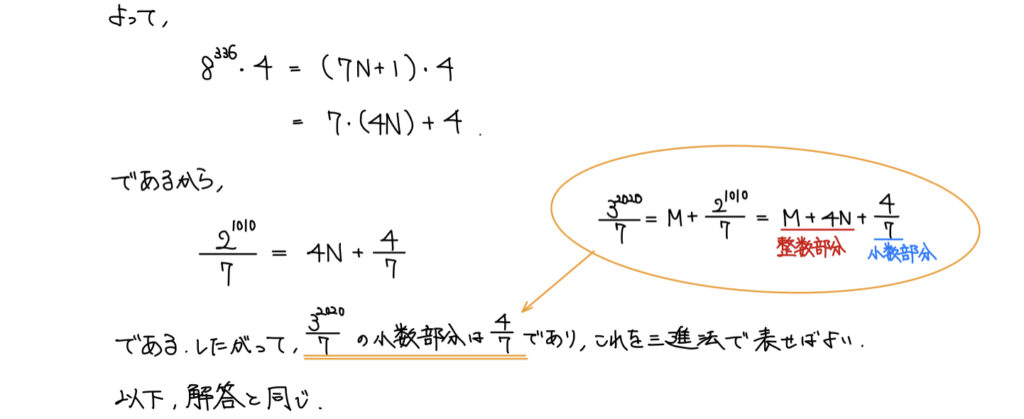
解説
実はやっている合同式の解法と変わらない。
なるべく丁寧な解説をするため、だいぶ冗長になってしまっている部分はある。
今回は二項定理を用いるにあたって、7を扱いたいという気持ちだけあれば上記のような解答になる。
合同式を知らなくてもこのように解けるが、ぜひ合同式を知って楽に解いてもらいたい。
さいごに
自分は初見では(3)が解けなかった。
凄く悔しい。
とはいえ、今は十分に納得しているため良しとしている。
間違えてしまっても、そこから学び、共通点を見つけて抽象化できたため解いてよかった。
今回の問題でn進数問題にだいぶ強くなったため、少し他国立大で探してみようかと思う。
好きな単元ではないが、面白い問題だった。
解いた方はお疲れ様でした。
これからも一緒に頑張っていこう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント