2020年度神戸大学の過去問を解いたので解答・解説をしていく。
今回は前期日程(理科系)の問題を解いた。
文科系の問題ではないことには注意してもらいたい。
それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『神戸大学 過去問』で検索してみて欲しい。
目安時間:18分
2020年度 神戸大学 前期日程 数学
[ https://www.office.kobe-u.ac.jp/stdnt-examinavi/wp-content/uploads/2020/08/03.suugaku_rikei.pdf ]
※上記URL:国立大学法人神戸大学HPホーム > 入試情報 > 学部入学案内 >入試問題及び出題の意図など > 2020年度一般入試(入試問題/出題の意図・評価ポイント/解答例)> 前期日程 数学 理科系 問題
※過去4年分が公式HP(下記URL)から閲覧できます。(2021年8月29日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人神戸大学HP>入試情報>学部入学案内>入試問題及び出題の意図など』
https://www.kobe-u.ac.jp/admission/undergrad/examin/index.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
神戸大学は偏差値55.0〜67.5の国立大学(2021年8月30日時点 パスナビ調べ)。
大問3は場合の数の問題だ。
難易度は日東駒専以上GMARCH以下レベルの問題だ。
和が30程度なので、樹形図や書き上げを駆使していけば求めることはできそうなため、難易度としてはだいぶ簡単かもしれない。
受験本番で方針が立たなければ数え上げよう。
和が高々30程度だ、そんな手間でもない。
ここでは基本解法でしっかり解いていくため、数え上げ以外の方法もしっかり押さえておこう。
それでは解答を見ていこう。
(1)場合の数、順列
解答

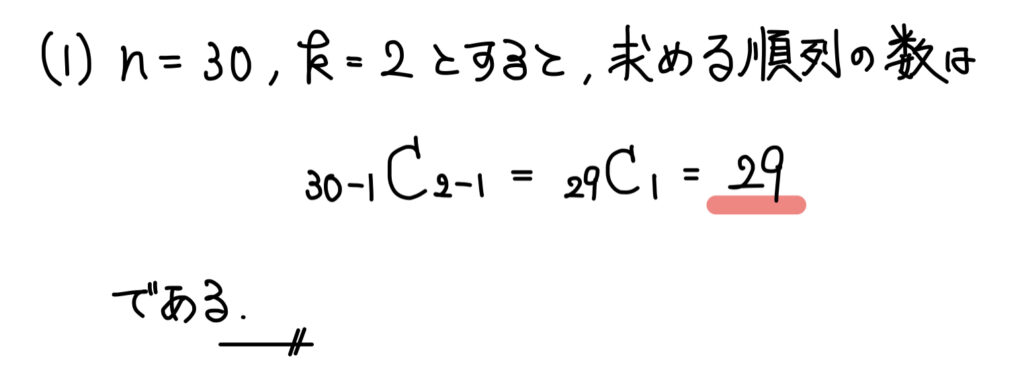
解説
場合の数や確率の単元において、もっとも重要なのが状況把握だ。
しかし、(そんなことは分かっているけど、それができたら苦労しない)というのが共通の悩みだろう。
状況把握のためには具体化(実験)してもいいし、表や図をかいてもいい。
色々な発想から考えていくわけであるが、1番意識して欲しいのは「今まで解いた基本問題と似ている(同じ)形はないだろうか」と探すことだ。
数学の発想が体系化されている人は、新しい状況を与えられてもすぐに数式化することができるが、凡人の自分にはそれが出来なかった。
そこで自分の知っている知識から何か引っ張り出せないかで悩むと良いことを知った。
新しい状況を数式化するのに時間をかけるのではなく、既知のもので参考になるものはないか知識の引き出しを探ることに時間をかけるのだ。
体系化できている人はこの引き出しを開けるスピードが尋常じゃなく速いのではないかと思う。
基本解法すら分からない問題は解けない問題は数え上げるか諦めることにしている。
さて、本題に話を戻そう。
今回「和が30」というのを見て(和を扱う場合の数の問題ってどんなのがあったかな)と考えた。
色々思い付いたが、その中の一つに「a+b+c=5となる負でない整数a,b,cの組は全部で何通りあるか」みたいな問題があったことを思い出した。
この問題の類題を全く見覚えないという人にはそもそも厳しい問題であったかもしれない。
(そんなのあった!)と思った人は解ける知識は十分にあるため、その引き出しを開ける訓練をしていけばいい。
既知の問題に似たものはないか、ぜひ考える訓練をしてみてほしい。
時間がもったいないということであれば(あの問題の形に似てる!)と思ったら簡単にメモし、解答を確認して方針があってたら飛ばすという勉強法でも良いかもしれない。
さて、これを思いついたらあとはこの問題でこの解法が適切かどうかを判断すればいい。
今回はこの方針で適切であることが分かるのが解答の冒頭だ。
自分はここに結構時間を費やしてしまったが、おかげで(1),(2)の計算自体はすぐに終わった。
(2)場合の数、順列
解答
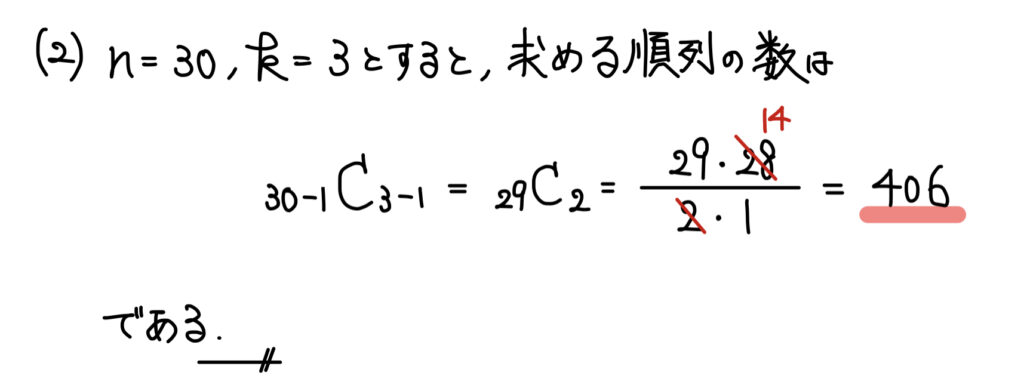
解説
(1)冒頭の式に代入して終了。
分からなければ「1つの数を1とすると…」という場合分けを沢山して求めればいい。
同じ数字が選ばれているかどうかには注意しよう。
(3)場合の数、組合せ
解答


解説
(2)と明らかに関連がある問題のため、「順列と組合せの違いは何か」というのを考えればよいのがこの問題のポイント。
順列と組合せの違いは「並べ方を考えるか否か」だ。
つまり、(2)において並べ方を考えない状況を答えればいい。
よって、ここからは「並べ方が被っているパターンは何でそれが何通りあるのか」に注目していけばいい。
そうすると自然と解答のような場合分けに行きつき、計算となっていく。
計算よりも数え上げが速そうな時は数え上げてしまおう。
また、場合の数に限った話ではなく、数学全体の話として「全体が求められたら全体から不要な部分引いて必要な部分を求める」という余事象的な発想は持っておこう。
さいごに
今回(1),(2)の一般化を考えられたのは気持ち良かった。
場合の数・確率は立式こそ難しいものの、計算自体は非常に簡単であるため計算力に自信がない自分にとってはとても好きだ。
これからも「知っている形はないか」に注目して解いたいこうと思う。
解いた方お疲れ様でした。
これからも一緒に頑張っていきましょう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント