高校数学で扱う図形の中に多角形がある。
多角形とは、簡単に言えば頂点とそれを結ぶ辺が存在する図形だと思ってもらえればいい。(厳密な定義は異なるが、今回はそこの厳密性は議論の対象ではないため小中学校の経験による知識で十分だ)
三角形や四角形、五角形などがその例だ。
今回は多角形の問題について、初等幾何の解法の発想を考えていこう。
多角形を分割
三角形への分割
多角形処理でまず考えるのが、三角形などの扱える定理・公式が多い形への分割だ。
多角形にはどこか1つ頂点を決めて、他の頂点に直線を引けば三角形に分割できるという性質がある。
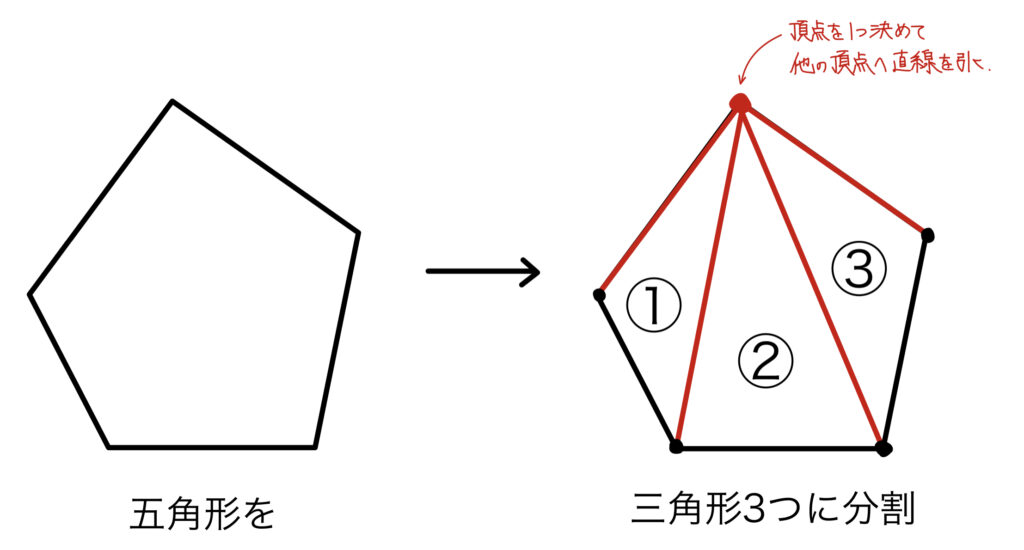
こうした性質から、多角形を扱う際には三角形に分割して、それぞれの三角形に着目すれば良いということになる。
例えば、五角形の辺の長さが知りたい場合、五角形を三角形に分割し、三角形の辺の長さを求めることで五角形の辺の長さを得る、といった感じだ。
自分達は小中高校で三角形や四角形について多く扱ってきた。
その一方で、六角形や七角形を多く勉強してきたという人は少ないだろう。
であれば、自分に一番馴染みやすい基本的なものに話を変換してしまった方が考えやすいのだ。
そのため、こうした五角形→三角形→五角形という論理展開で求めたい値を手に入れていくが多い。
三角形に分割しても考えづらい場合
直角三角形への分割
三角形に分割しても難しい場合、話をさらに扱いやすい形に変えていく必要がある。
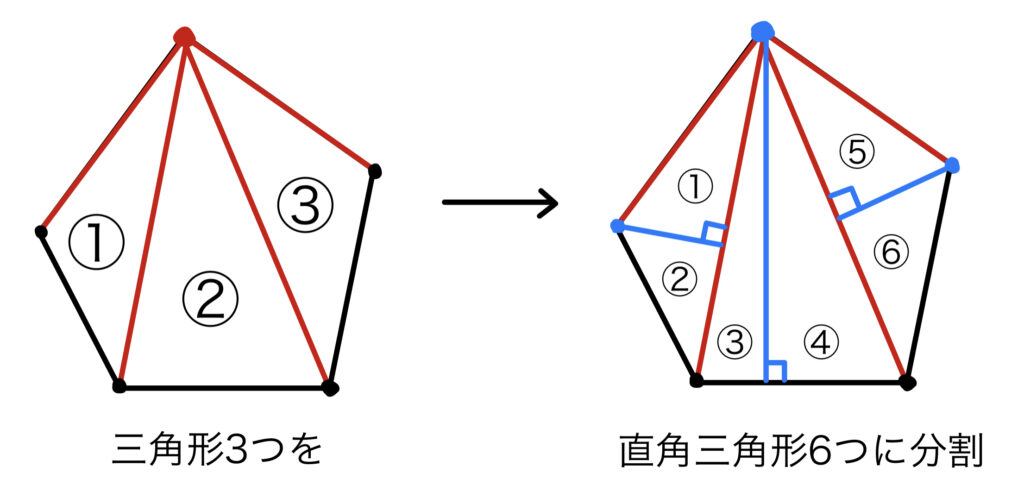
三角形は頂点から垂線を下ろすことで直角三角形を作ることができる。
直角三角形の方が三平方の定理の利用や円の直径の利用、初等幾何ではないがベクトルの内積の利用と扱える定理・公式が増えるため考えやすくなる。
つまり、多角形を分割して行き着くのは直角三角形なのだ。
直角三角形以外の分割(作図)
直角三角形でも困難な場合に考えるのは以下の2つだ。
- 二等辺三角形を作る
- 有名角(30°,45°,60°)で線を引く
これらも図形の性質や相似、三角比などが扱いやすいためよく考える。
これは難関中学受験や高校受験でも多く見られる処理だ。
問題文で具体的な角度を与えられた場合の最終兵器として、二等辺三角形や有名角を使いたい!と思えるようになろう。
中点を与えられたら
図形問題で中点を与えられた問題で、解答作成が困難な場合の最終手段として中点への直線を延長するというものがある。
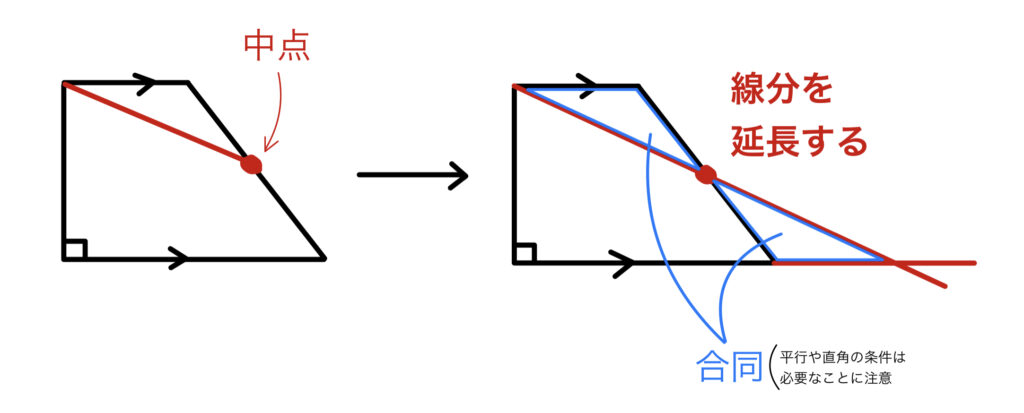
線分の中点ということは、そのまま中点を通過して三角形などの図形が新しく作れれば、辺の比だったりで相似や合同、中点連結定理など色々やれることが増える。
同じく内分する点も延長する発想を持っとくことは重要だ。
さいごに
今回は簡単に多角形問題の初等幾何での処理を考えた。
三角比を学び,正弦定理や余弦定理といった力技を覚えた高校生からはこの手の発想はどんどん抜けていく。
色々学んだことを忘れずに新しい知識も吸収していくことが重要だ。(それが簡単にできれば苦労はないのだが…)
実際に問題で扱えていないため問題への活用のイメージは作りづらいかもしれない。
自分としては、今後入試問題の解答解説を扱った際にこの発想のイメージは必要なためここで触れておいたといった感じだ。
これから実際に入試問題の解答解説で分割した際にはこのページのリンクを貼ろうと思う。
このページも必要に応じてより精度の高いものに更新していく予定だ。
基礎こそ重要。



コメント