2020年度 小樽商科大学の過去問を解いたので解答・解説記事をしていく。
早速見ていこう。
問題(大問4)
※現在問題は非公開とさせていただいております。
過去問題は大学公式の問い合わせホームから直ちに請求できます。
費用もかかりませんので是非行ってみてください。
年度により請求できないものもあります。
公式サイト『国立大学 小樽商科大学 受験生サイト-過去問題請求ホーム』
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
全体概評
小樽商科大学は偏差値50の国立大学(偏差値はパスナビ調べ)。
難易度としては難問ではなく、典型的な問題と処理で解ける。
大問4は小問3つで構成されている。
この問題は多くの受験者が解けるであろうため、落とさないようにしたい。
(1)三角形の相似の証明
解答
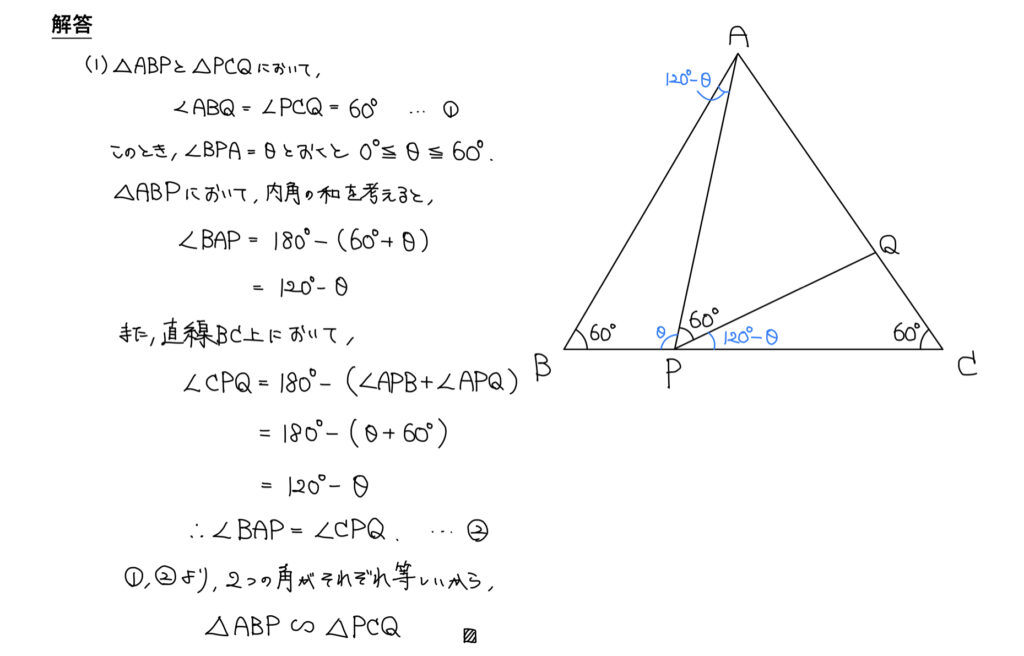
解説
三角形の相似の証明といえば高校入試の定番だ。
一般に、三角形の相似の証明は以下のいずれかで示される。
- 2組の辺の比とその間の角がそれぞれ等しい
- 2組の角がそれぞれ等しい
- 3組の辺の比がそれぞれ等しい
今回は明らかに60°の共通が見えるため、残りの角を示しにいこうかなと考えて文字θでおく。
文字で置いたら変域注意は必ずチェックしておきたい。
(2)面積の最大値問題
解答

解説
面積の最大・最小問題は基本的には関数の最大・最小問題に持っていく。
今回も面積を変数で表し、関数の最大・最小問題に持っていく流れだ。
60°が見えているため、「2辺と間のサインなす角」の面積公式の利用を考える。
あとは2辺を変数で表せば良い。
どこを変数に置くかは自由だが、(1)の利用を考えた時に相似比がなるべく簡単なようにおきたいと思えると良い。(当然どこを置いても求まることは求まる)
変数でおけたら3次整関数の最大・最小問題であるから、微分して増減表で終了だ。
さいごに
難易度としては、日東駒専を受ける人で解ける人は多いという問題ではないだろうか。
(2)のみ出題された場合には正答率も下がりそうだが、(1)がかなり助けになっているという印象だ。
これが解けなかった人は、相似を用いた図形問題の基礎問題からやり直しても良いかもしれない。
解けた人はしっかりとした方針決めができているため、もう少し偏差値の高い大学の過去問を解いてみても良いかもしれない。
中学数学が全然定着していない自分は、図形問題に対して苦手意識がある。
補助線や相似を考える問題は常にそう考える理由を探しながら解いていくと他の問題にも応用ができて良い。



コメント