2020年度 富山大学の過去問を解いたので解答・解説記事をしていく。
今回解答・解説をするにあたり、理系の前期入試を扱っているのには注意してもらいたい。(文系及び後期入試ではない)
早速見ていこう。
問題(大問1)
目安時間:40分
2020年度 富山大学 前期日程 理学部 数学
[ https://www.u-toyama.ac.jp/wp/wp-content/uploads/02zenki-05.pdf ]
※上記URL:国立大学法人富山大学HP 過去問ページより 2020年度 前期日程 理学部数学
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。参考URL『国立大学法人富山大学HP-過去問題-』
https://www.u-toyama.ac.jp/admission/undergraduate-exam/past_exams/
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
富山大学は偏差値47.5〜62.5の国立大学(2021年6月3日時点 パスナビ調べ)。
最低偏差値の工学部と最高偏差値の医学部を合わせた偏差値のため,全然参考にはならない。(工学部を下に見ているわけではない)
問題としての難易度はGMARCH程度だろうか。
難問というものは特になく,基本的な問題を複合しているといった感じだ。
ゆえに基礎が分かっていないと解ける問題は少なくなってしまいそうだ。
大問1はテーマが1つのそれに付随する小問4つで構成されている。
こういった同一テーマの問題は小問を上手く誘導として扱っていきたい。
今回もしっかり誘導になっているので,状況を把握しながら解いていこう。
(1)直線の方程式
解答

解説
x,y,z軸からなる空間において2点が与えられ、2点を通る直線を考えるというところから問題は始まる。
「通る2点→代入可能」という発想から直線の方程式を考えることになるが、その際に方針は数Ⅱの直線の方程式(①)と数Bの空間ベクトル(②)どちらでアプローチしようかと瞬時に引き出せるようにしておきたい。

自分は①でのアプローチで示した。方針さえ決まれば後は「xy平面上ってことはz成分が0」といった簡単な処理で解ける。
最初の方針決めだけ把握しておけば解ける問題だ。
小樽商科大学の大問1(1)に類題があったため、貼っておく。
類題 → 「68話 2020小樽商科大学 過去問大問1【解答解説】」
(2)媒介変数の文字消去
解答
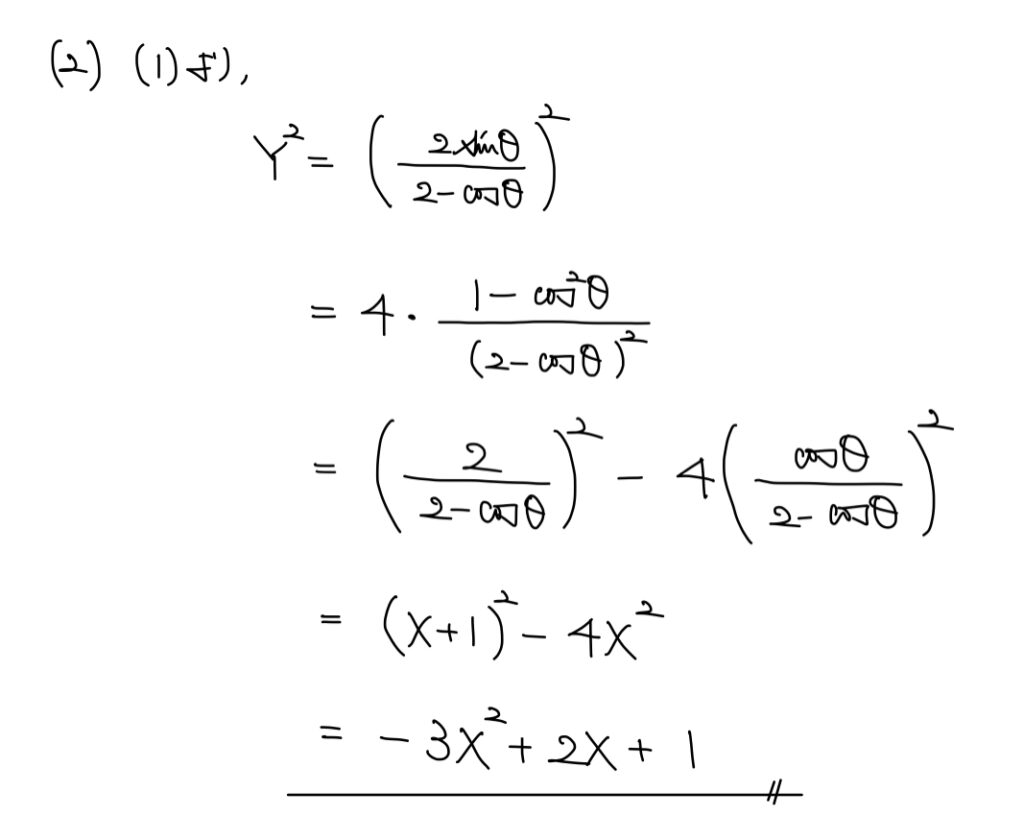
解説
(1)でX,Yをそれぞれθで媒介変数表示したため、そこから媒介変数を消去してXとYの関係式を得るという問題。
今回媒介変数θは三角比とともに用いられているため、三角関数で表示されている。
三角関数で文字を扱う際には「2乗を作りたい」という思考が重要だ。
根拠としてはsin2θ+cos2θ=1や他の三角比の相互関係を利用したいというところにある。
上手く2乗の形を作りながら変形していく。
変形の仕方は色々あるため、試してみると面白いかもしれない。
ただし、どれも「2乗を作りたい」という思考のもと式変形されるため、重要な考えは「2乗を作りたい」でしかない。
(3)2次曲線のグラフ
解答
解説
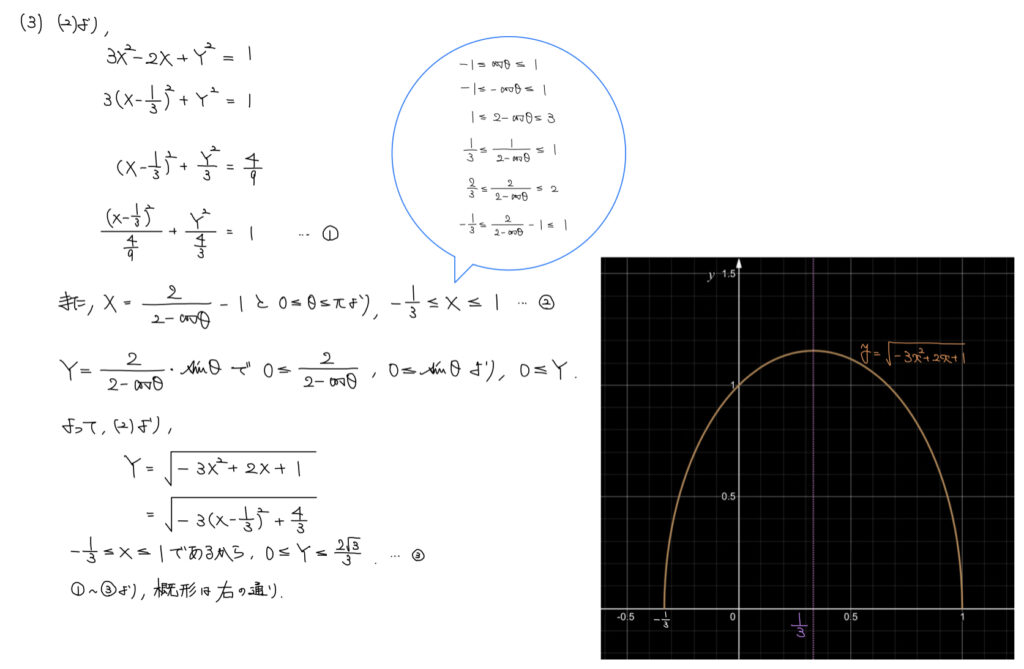
(2)よりxとyの関係式が得られたため、それを図がかけるように式変形をしていく。
xの次数が2、yの次数が2というところから、楕円か双曲線であることが予想でき、xとyの正負が一致しているため楕円であることが分かる。
あとは式変形を丁寧にしていくだけ。
自分はとりあえず右辺が1である状況を作り、楕円をイメージしながら式変形をして、ある程度ゴールが見えたら一気に楕円の形に持っていくという形で式変形をした。
その後、グラフをかくためにxとyの変域が知りたいという思考の流れになり、(1)の媒介変数表示から求めていく。その際に、0≦θ≦πからアプローチしていくのだろうなということは思いつくようにしておきたい。
最初にxの変域が求まり、その流れでyの変域を求めていくのだが、(2)の段階ではy2とx2の関係式であるからy=±√(xの式)という形になってしまう。
そのため、±の両方存在するのかというところから、まずyの正負について考える必要がある。
yが正であることが分かるため、y=√(xの式)としてyの変域を求めていけばよい。
あとは楕円とx,yの変域という得られた情報から図示をしていく。
yの変域を求めるというところで減点が多そうな問題であったような気がする。
(4)回転体の体積
解答

解説
(3)まででグラフもかけているため、回転体の体積の公式(考え方)さえ知っていれば容易な問題。
計算ミスにだけ注意したい。
さいごに
公式の模範解答はこちら
https://www.u-toyama.ac.jp/wp/wp-content/uploads/r02_A-06.pdf
参考URL:国立大学法人富山大学HP 「過去問題」ページより 令和2年度 前期日程 理学部数学 解答例等
問題を解いた印象としてはGMARCHの受験者には一定数が解ける人がいて、日東駒専の受験者には難しく正答率がだいぶ低めになりそう、という印象だ。
問題集通り典型問題のままというわけではないが、問題集でトレーニングを積んでいれば処理は思い付くというレベルだ。
様々な単元の複合問題になっているが、分解して考えれば処理自体は各単元の基本処理だ。
おそらく難易度的にも二次曲線という単元的にも(3)が鬼門なのではないだろうか。
解けた人はそれぞれ問われていることに対しての方針決めがしっかりとできているため、もう少し偏差値の高い大学の過去問を解いてみても良いかもしれない。
自分としては二次曲線が苦手なため、よい復習問題になった。
こういった流れのある問題は楽しい。
国公立の問題が好きなのかもしれない。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント