2020年度 富山大学の過去問を解いたので解答・解説記事をしていく。
今回の解答・解説は理系の前期入試を扱っているの点は注意してもらいたい。(文系及び後期入試ではない)
早速見ていこう。
問題(大問2)
目安時間:30分
2020年度 富山大学 前期日程 理学部 数学
[ https://www.u-toyama.ac.jp/wp/wp-content/uploads/02zenki-05.pdf ]
※上記URL:国立大学法人富山大学HP 過去問ページより 2020年度 前期日程 理学部数学
※過去3年分が公式HP(下記URL)から閲覧できます。掲載終了している可能性もあります。
参考URL『国立大学法人富山大学HP-過去問題-』
https://www.u-toyama.ac.jp/admission/undergraduate-exam/past_exams/
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
富山大学は偏差値47.5〜62.5の国立大学(2021年6月3日時点 パスナビ調べ)。
最低偏差値の工学部と最高偏差値の医学部を合わせた偏差値のため,全然参考にはならない。(工学部を下に見ているわけではない)
問題としての難易度はGMARCH程度だろうか。
難問というものは特になく,基本的な問題といった感じだ。
おそらく大問3つの中で完答率が高いのは大問2ではないだろうか。
大問2は小問3つで構成されている。
各問はバラバラとはいえ、明らかに(3)は(1),(2)と誘導になっているためそこは気付くようにしたい。
条件をどこで使うのか、どうしたら使えることができるのかを考えて解いてこう。
(1)不等式の証明(因数分解)
解答
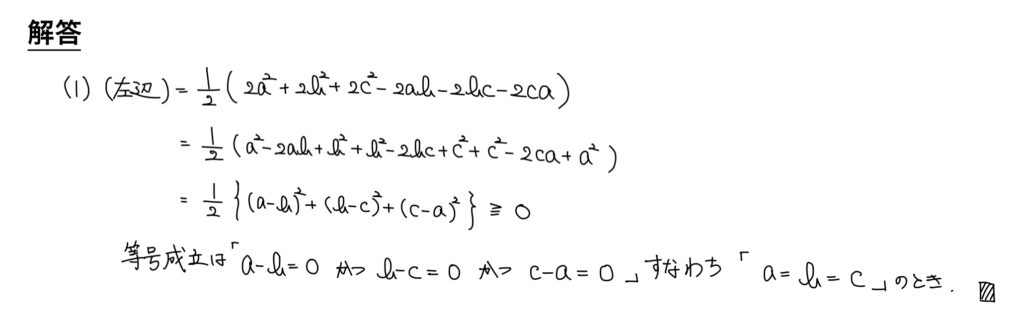
解説
特に条件はなくa,b,cは実数であるというところから「2乗や絶対値を作りたい」と考えよう。
実はこの問題のような分母分子2倍するというのはよくある式変形なので知っておこう。
仮にこのテンプレの式変形の発想がなかったとしても「2乗を作りたい」と思えば乗法公式を作るために必然的に分母分子2倍するということになる。
自分もあまりテンプレを意識せずとも分母分子2倍していて、(そういえばこういう処理あるあるだったなぁ)と思った程度だ。
2乗が作れれば証明され、等号成立は各2乗が全て0になるときだ。
(2)不等式の証明(因数分解)
解答

解説
「A≧B」の不等号証明の基本的な処理は「A-B≧0」を示すことだ。
今回分母を払うために両辺(a+b+c)(a4+b+c)倍するのだが、その際に各因数の正負のチェックは必須だ。
今回は条件より各因数の正が言えて、不等号の向きが変わらない。
あとは式変形をしていく。
多項式の状態で大小比較は難しいため、因数分解になる。
因数分解は最低次数の文字(b,c)で整理して示すことができる。
等号成立は各因数が0のとき。
(3)不等式の証明
解答
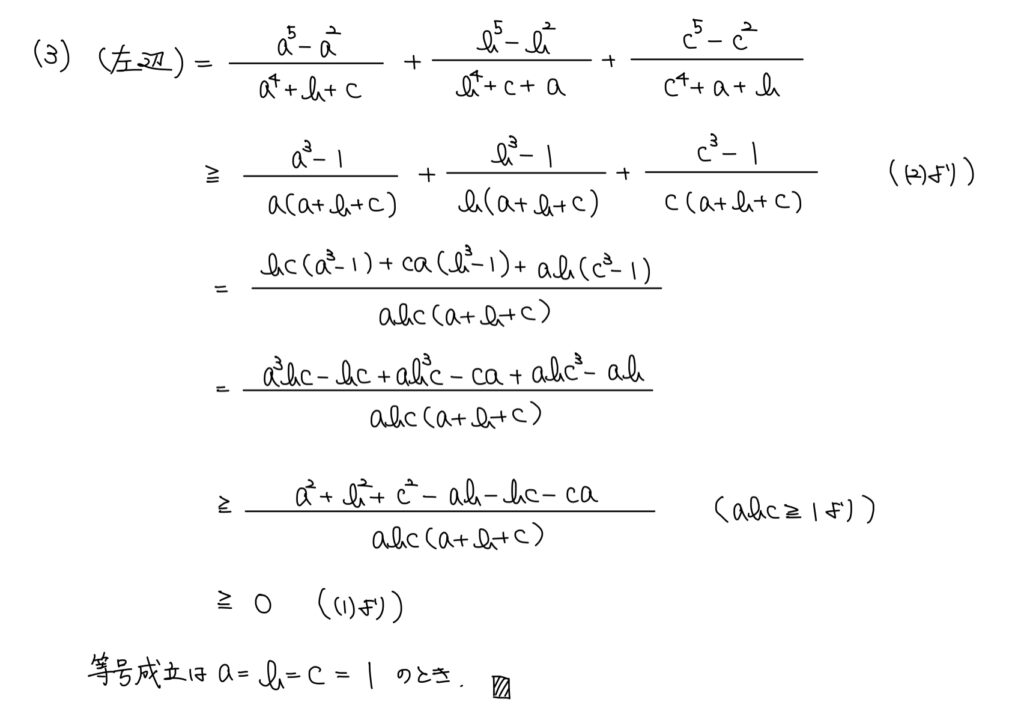
解説
明らかに(2)を利用して示すため、条件を確認しながら(2)を利用する。
あとは分数の和と差のため通分。
そうして計算すると(1)が見えてくるため、(1)の利用。
(2)さえ解けていれば(3)はそんなに難しくない。
さいごに
公式の模範解答はこちら
https://www.u-toyama.ac.jp/wp/wp-content/uploads/r02_A-06.pdf
参考URL:国立大学法人富山大学HP 「過去問題」ページより 令和2年度 前期日程 理学部数学 解答例等
難易度としては、東京の私立で言えばGMARCHを受ける人はこれくらい解けていて、日東駒専を受ける人には少し難しく感じそう、という印象だ。
問題集通り典型問題のままというわけではないが、問題集でトレーニングを積んでいればすぐに処理は思い付くというレベルだ。
解けなかった人はしっかりと因数分解や不等式の証明のトレーニングを積んでいこう。
個人的には(3)を解くために(1),(2)の利用を考える形式が好きなため楽しい問題だった。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』



コメント