2020年度 東京電機大学の過去問を解いたので解答・解説をしていく。
今回解答・解説をするにあたり、数学Ⅲを含む問題の前期入試を扱っているのには注意してもらいたい。(数学Ⅱ・Bまでの入試ではない)
早速見ていこう。
問題(大問3)

まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
東京電機大学は偏差値42.5〜55.0の私立大学(2021年6月13日時点 パスナビ調べ)。
問題としての難易度は日東駒専レベルだろうか。
難問というものは特になく、教科書レベルの基本的な問題だ。
大問3はこの年の問題の中では一番難易度は高いかもしれない。
一問一問基本的な解法になるため、しっかり知っておきたい。
(1)接線の方程式
解答
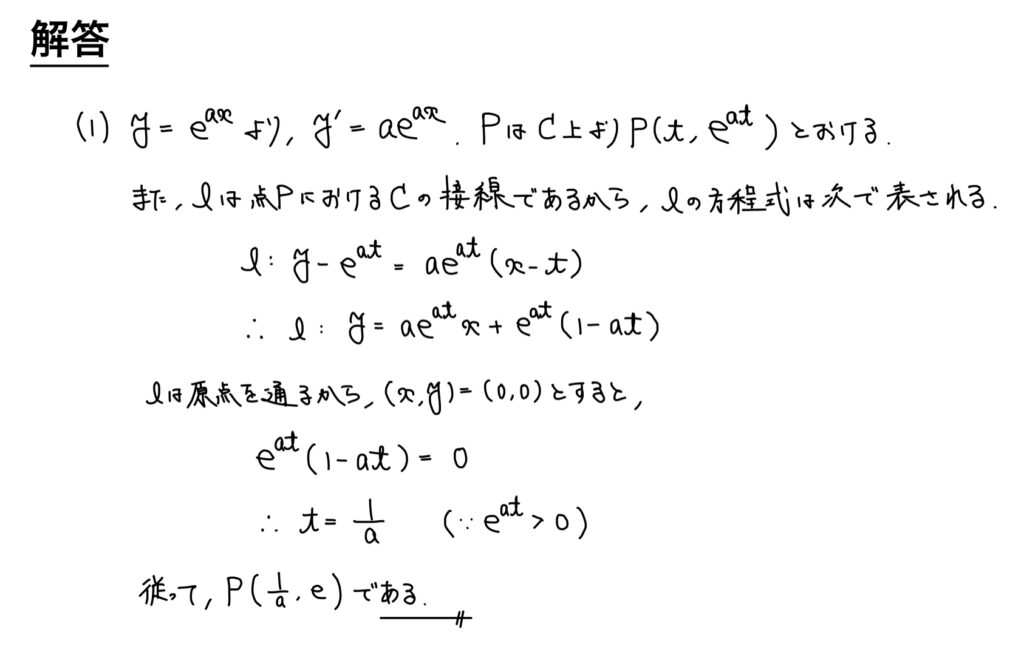
解説
Pの座標を問われているから、Pの座標を文字でおいてアプローチしていく方針だ。
では、どう文字で置くかだが、文字を設定する際に重要なのが極力文字が少なくなるようにおくということだ。
なんでもかんでもx、yとしてしまっては最後に文字消去する際、多くの連立方程式を解くことになってしまう。無駄に煩雑になってしまい、代入ミスが符号ミスの原因ともなってしまう。
そこで、文字数を減らすためにPの条件を探すわけだが、今回のPの条件は「 C 上 かつ l 上」であることから考えることができる。
まず、PはC上より、x座標(ここでは t )さえ設定すれば、y座標はCの方程式に代入して得られる。(文字の個数を少なくおくことができた)
あとは t を求められればPの座標は求まる。
次にPは l 上を考えるわけだが、「PはCと l の接点」であるという条件は「lはCの点Pにおける接線」と言い換えることができる。
l は「Cの点Pにおける接線」という基本的な問題を解くことで得ることができる。
あとは l は原点を通るという条件から t が求まり、Pの座標を求めることができる。
ごちゃごちゃしていて何をしたら良いのか分からなくなりそうだが、結論は「Pの座標を求めたい」、そしてそのPは「C上かつ l 上」というところをブレなければ見やすくなるのではないだろうか。
(2)定積分
解答
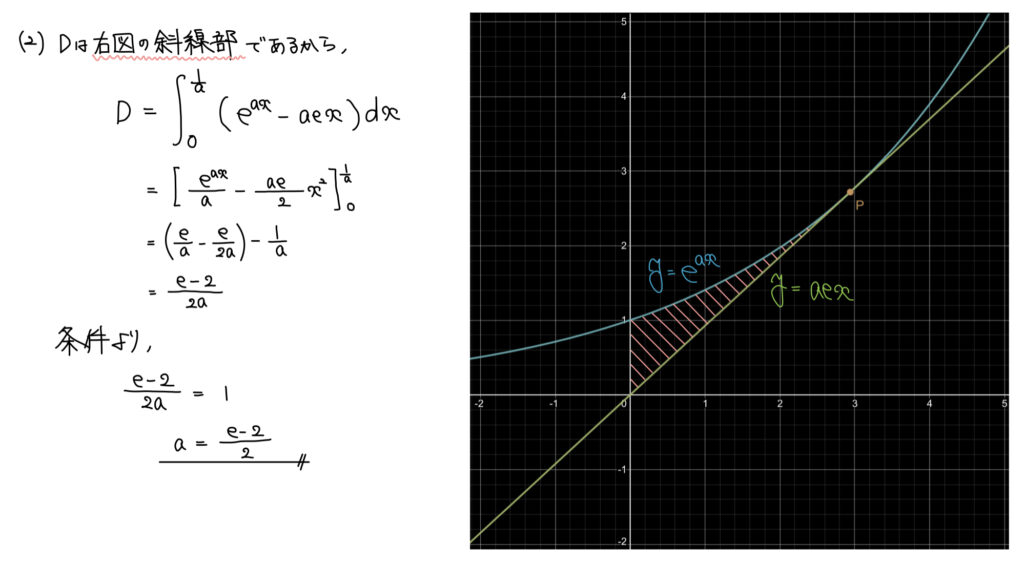
解説
(1)が求まって簡単に図示をすると上のようになる。
あとは単純に定積分の計算をし、それが1となるようなaの値を求めれば良い。
定積分も直接求めることができるため、ポイントは図示して考えたかと定積分の計算を間違いなくできるかというところだ。
(3)回転体の体積
解答
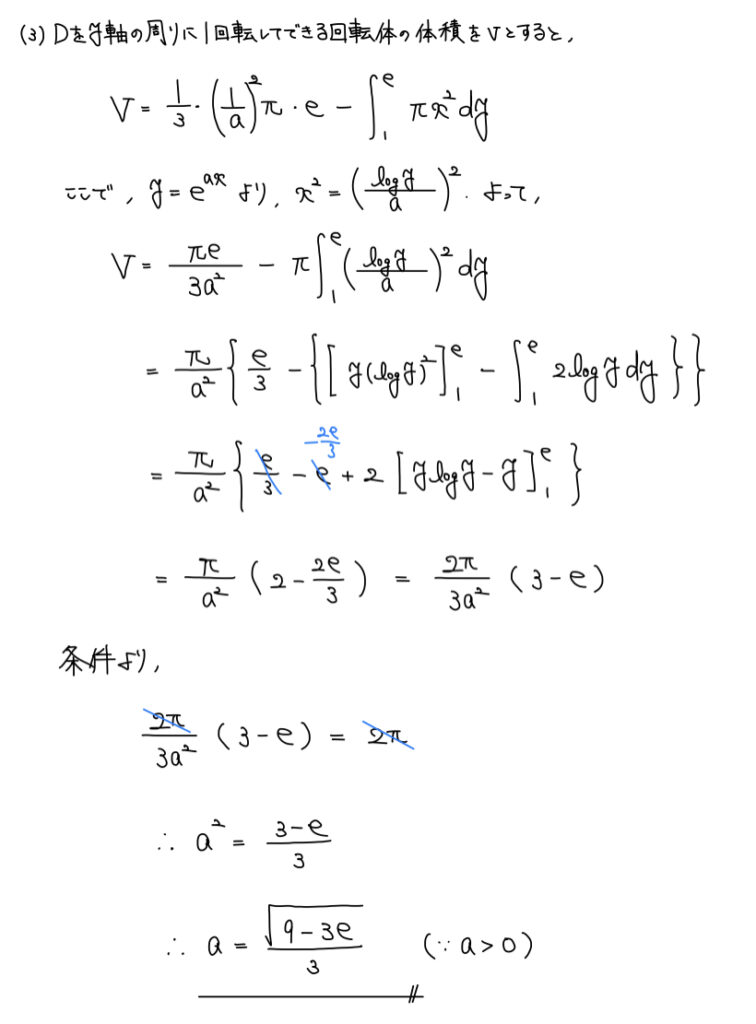
解説
今回はy軸周りの回転体ということでどんな図形かをイメージをしてみる。
すると、直接の計算で求めることが難しそうなことに気付く。
直接求めることが難しい場合は、求めることのできる部分を求めて、足したり引いたりするということを考える。
この考え方は面積や体積を求める際のよくある手法なので知っておこう。
今回も三角錐を求めて、不要な部分を比くということでも止めることができる。
さいごに
問題を解いた印象としては、2020年に関しては日東駒専よりわずかだけ難しいという印象だ。
とはいえ、基本問題であることには変わらないため、日東駒専志望の人は練習として解いておいてもよいと思う。
GMARCH以上志望の人は解けなければいけない難易度だ。
一つ一つは問題集通りの典型問題と言えるため、解けなかった人は問題集でトレーニングを積んでいこう。
どんな基本問題がくっついているのか、そのくっつきはどの問題文の一文から読み取れるのかを意識してみるととても良いのではないだろうか。
東京電機大学、面白い問題でした。
またいつか、昨年度の問題も解いてみようかな。



コメント