ベクトルの問題について扱う「ベクトル道場」シリーズ。
今回解いたのは「2020年度 北海道大学(前期) 大問1」だ。
難易度目安【易 ★★★☆☆ 難】
では見ていこう。
問題

まずは解説より先に問題を解いてもらいたい。
分からなかった人は解説を見てもらって、方針を参考にした上でどこから解けていないかを炙り出してもらえれば嬉しい。
では、問題解くの頑張って!
〜答案作成中〜
お疲れ様でした。
それでは、解答解説を始めていこう。
概評
難易度は東京の私立でいえば「GMARCH志望者は解けておくべき」というレベルだ。
日東駒専志望で解けていれば力がある方といえるのではないだろうか。
学校で配られるような標準的な薄い問題集でも解いていれば完答もできそうだ。
そんな基礎がしっかり詰まった問題であるため、解けなかった人はしっかり復習することで知識や理解の穴が埋められそうだ。
それでは、一問一問楽しみながら見ていこう。
(1)平面ベクトルの内積
解答
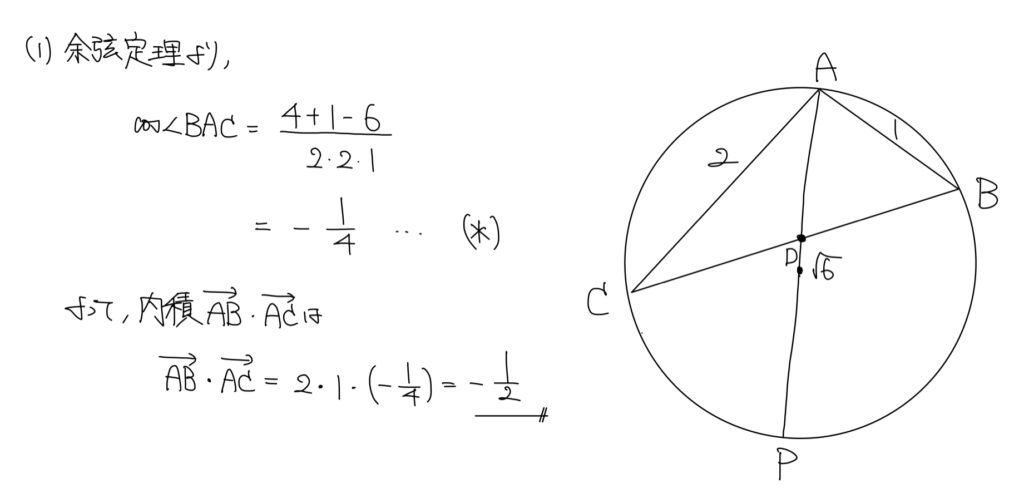
図は自分が解いた際に描いたもの。正しくはないです。
解説
ベクトルの内積ということで考えるアプローチ方法は以下の4つ。
- 大きさとなす角
- 成分(同一成分の積の和)
- 大きさの2乗
- 正射影
今回はなす角求めて「①大きさとなす角」で解くか辺の長さ、つまりベクトルの大きさが与えられているため「③大きさの2乗」で解くかのどちらかでいいだろう。
解答は「①大きさとなす角」で解いた。
なす角を求めるために「3辺1角の問題」のため余弦定理を用いた。
※辺が3つ角が1つで、その内3つ明らかで1つ不明の場合は余弦定理が有効
(2)平面ベクトルの内積
解答

解説
「外接円の中心」を通過するためAPが直径であることは把握できる。
直径の条件の使い方については「円のベクトル方程式」で扱う。
直径の両端点から円周上の点への2つのベクトルは直交する、というものだ。
そして、「直交」すなわち「垂直条件」が与えられたら迷わず「(内積)=0」で処理しよう。
また、円周上の点はAとPの他にBとCしかないため、それらを利用すればよい。
あとは始点の統一を意識しながら式変形して解けばよい。
(3)平面の位置ベクトル
解答

解説
まず点Dの位置ベクトルを求めにいく。
点DはBC上かつAP上なのでそれで式が2つできる。
BC上は内分点処理、すなわち、係数の和が1で表せばよい。
AP上は同一直線上処理、すなわち、実数(k)倍で表せばよい。
一次独立であるからそれらの係数比較で文字定数が求まり、Dの位置ベクトルが分かる。
Dの位置ベクトルが分かったため、あとはベクトルの大きさを求めればよい。
(3)別解
解答
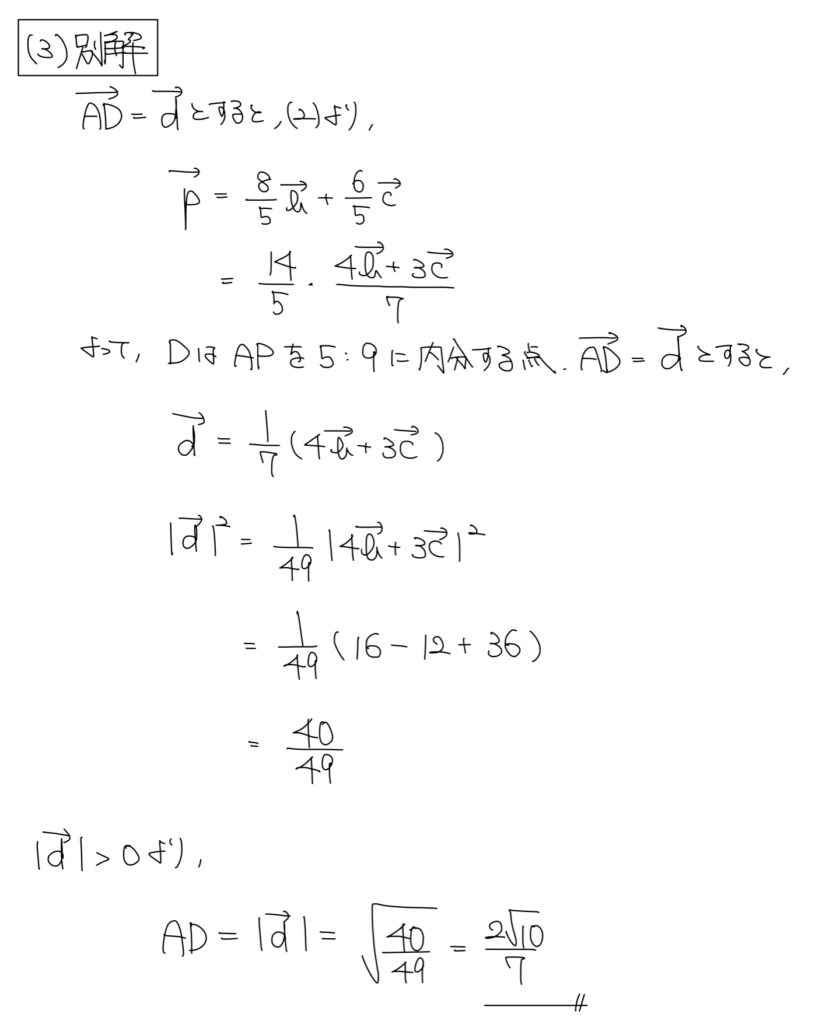
解説
点DはBC上かつAP上のため、点Pの位置ベクトルを線分BCに内分するように式変形することで点Dの位置ベクトルを得ることが出来る。
同一直線上かつ分点の状況ではこの別解の形が有効。
あとは得た点Dの位置ベクトルの大きさを求めれば終了だ。
さいごに
旧帝大ということで少し臆していたが、普通に解けて嬉しかった。
なぜその式変形をしたのか、状況ごとにどういう解法が有効かを言えるようにしていきたい。
何か解答不備などあったらコメントで教えてもらえればありがたいです。
一緒に頑張っていこう。
※無断転載や商業目的の利用は控えていただきますようお願いします。



コメント