ベクトルの問題について扱う「ベクトル道場」シリーズ。
今回解いたのは「2020年度 東北大学(前期入試:文・教育・経済(文系)・医) 大問4」だ。
難易度目安【易 ★★★☆☆ 難】
では見ていこう。
問題

まずは解説より先に問題を解いてもらいたい。
分からなかった人は解説を見てもらって、方針を参考にした上でどこから解けていないかを炙り出してもらえれば嬉しい。
では、問題解くの頑張って!
〜答案作成中〜
お疲れ様でした。
それでは、解答解説を始めていこう。
概評
難易度は東京の私立でいえば「GMARCH志望者は解けておくべき」というレベルだ。
日東駒専志望で解けていれば力がある方といえるのではないだろうか。
(1)、(2)の正答率はかなり高いだろう。
(3)を解けるかどうかが分かれ道となりそうだ。
解法は基本通り行えばいいため、初見の形の問題でもいつも通りの方針で解いていこう。
それでは、一問一問楽しみながら見ていこう。
(1)平面ベクトルの演算
解答
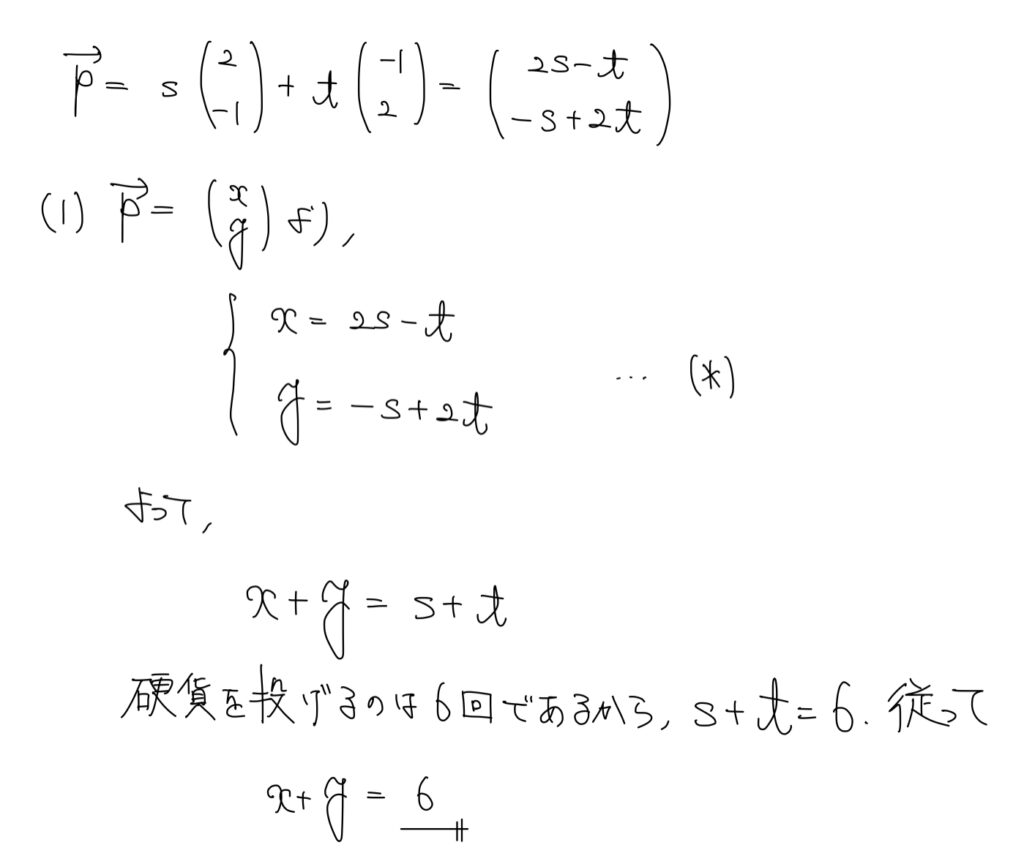
解説
まず、ベクトルpを2通りの表記で書かれているため、等式を整理しておこう。
整理することでx、yの式をs、tの式へと変換。
sとtは表と裏の回数であるから、和が6となる。
今回触れなかったが、あらかじめs+t=6よりt=6-sとして文字数を減らしておくのがよいだろう。
(2)平面ベクトルの演算、反復試行の確率
解答
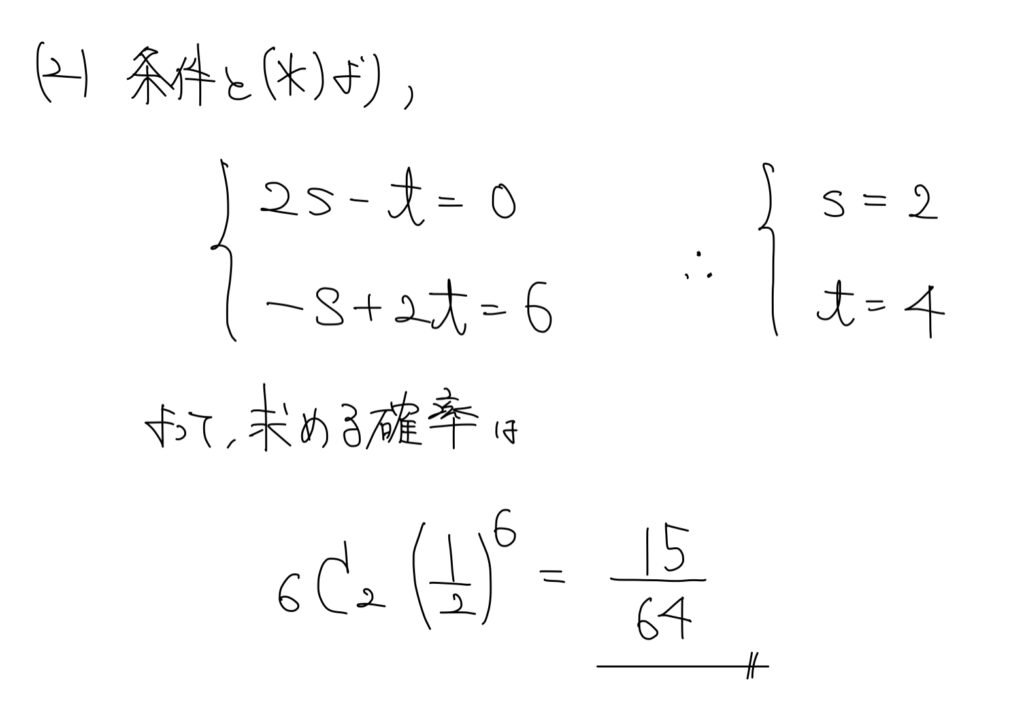
解説
(1)同様ベクトルpの成分についての話。
sとtの話に変換して連立方程式へ。
sとtが具体的に求められれば、硬貨の表が出る枚数と裏の出る枚数が分かるため、ここからはただの反復試行の確率の問題となる。
(3)平面のベクトルの内積
解答

解説
ベクトルの内積ということで考えるアプローチ方法は以下の4つ。
- 大きさとなす角
- 成分(同一成分の積の和)
- 大きさの2乗
- 正射影
今回の問題はなす角が与えられているため、処理は「1.大きさとなす角」で確定。
成分も得られているため、内積求めることができる。
大きさや内積は事前に求めておくとよいだろう。
その後はベクトルのなす角の条件を考えていく。
ベクトルのなす角はcosで考えるため、三角関数の不等式、そして不等式の証明へと単元転換が行われていく。
その際、sとtの2変数の不等式証明となると話が複雑になるため、可能であれば変数を減らした方がよい。
今回はs+t=6よりt=6-sとして文字数を減らしておくのがよいだろう。
また、不等式証明において、今回のように少数の有限個のパターンを考えればいい場合は直接代入で調べるほうが良いだろう。
高々6つの候補を調べるくらいであれば、わざわざ漸化式を作る必要もないだろう。
こうして不等式を満たすsとtが分かり、反復試行の確率と確率の加法定理より解答できる。
さいごに
旧帝大ということで少し臆していたが、普通に解けて嬉しかった。
東北大学の合格者で(1),(2)が解けていない人はいないのではないだろうか。
自分にとって内積問題は大好物のため、難易度は高くなくても自分に力があるような感じがして嬉しい。
これからもどんどんベクトルを解いていこう。
何か解答不備などあったらコメントで教えてもらえればありがたいです。
一緒に頑張っていこう。
※無断転載や商業目的の利用は控えていただきますようお願いします。



コメント