2020年度 金沢大学の過去問を解いたので解答・解説をしていく。
今回解答・解説をするにあたり、前期日程を扱っている点には注意してもらいたい。(後期日程ではない)
早速見ていこう。
問題(大問4)
目安時間:30分
2020年度 金沢大学 前期日程 数学(理系)
[ https://www.kanazawa-u.ac.jp/wp-content/uploads/2020/04/02-2-2sugaku_rikei_zenki.pdf ]
※上記URL:国立大学法人金沢大学HP 「過去問題及び正解・解答例」ページより 令和2年度入試 前期日程 理系数学
※過去3年分が公式HP(下記URL)から閲覧できます。2020年度分が掲載終了している可能性もあります。
参考URL『国立大学法人金沢大学HP-過去問題-』
https://www.kanazawa-u.ac.jp/education/admission/kakomondai
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
金沢大学は偏差値50.0〜65.0の国立大学(2021年6月17日時点 パスナビ調べ)。
個人的には2020年はこの大問の完答が最難関なように感じる。
(1),(2)までは解ける人が多いように思う。
解けなくても、方針はなんとなく見えるのではないだろうか。
問題は(3),(4)だ。
受験生の多くが苦手であろう逆関数だ。
この逆関数で正答できるとかなり他の受験生に差がつけられるのではないだろうか。
全てが解けなかった方、ぜひ一緒に解き直しをしていこう。
(1)関数の単調性
解答
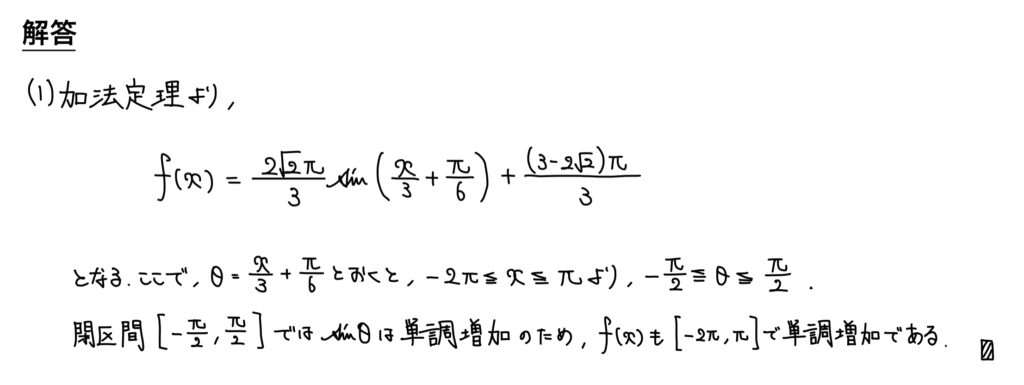
解説
まず、問題文のsinとcosの同角一次式(角度が同じで1次の三角関数)から合成を考える。
合成をするとsinの関数で考えることでき、あとはこの関数の単調増加を示せばよい。
微分して正で示すのが通常だが、元の関数からもいうことができるため今回は元の関数で示した。
不安な方は微分して示すのが一般的なため、そちらで示そう。
(2)関数の大小関係
解答
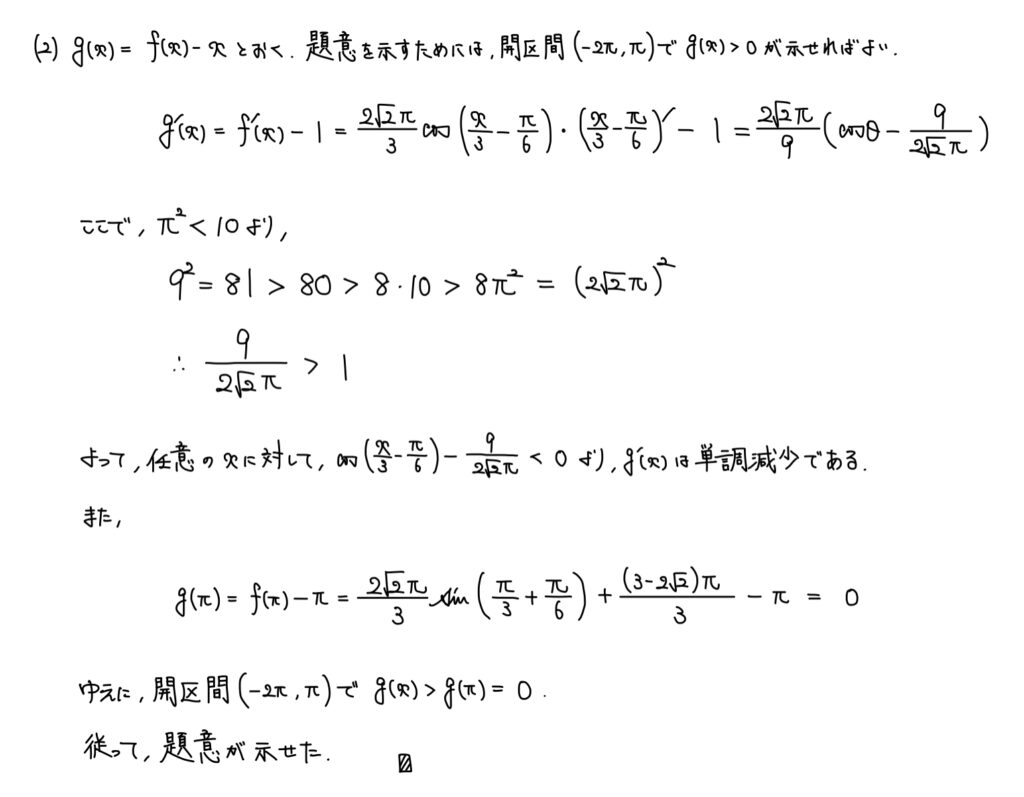
解説
関数の大小関係は定数分離(0を分離)して考えるのが定石。
定数分離して新しく関数を設定。
あとは定数と関数の大小関係、すなわち関数の最大・最小問題と変換することができる。
例えば、全ての実数xでf(x)>aを示すためにはf(x)の最小値がaより大きいことを示せばいいということだ。
今回も同様。
g(x)を設定し、定義域内でg(x)>0が言えればよい。
そのためには定義域内でg(x)の最小値が0より大きければいいため、g(x)の最小値を調べにいく。
関数の最大・最小と言えば微分して増減表、それでも不明であれば再度微分して調べていく。
今回は一度の微分で調べられる。
条件の使い方だが、①「平方根が見えて」かつ②「正の数」の大小のため2乗する発想に至った。
(3)逆関数の積分
解答

解説
(1)より、元の関数f(x)が単調増加のため、逆関数f-1(x)も単調増加であることが言える。
あとはなるべく元の関数の形で微分をしたいため、どうにかして分かる形に変形することを考える。
この辺りは逆関数を丁寧に見ていき&求めたい積分の形を意識することで、元の関数を交えた形に変形していく。(変形できていく)
逆関数がないように変換できたら、あとはただ積分するだけだ。
(4)積分と面積
解答
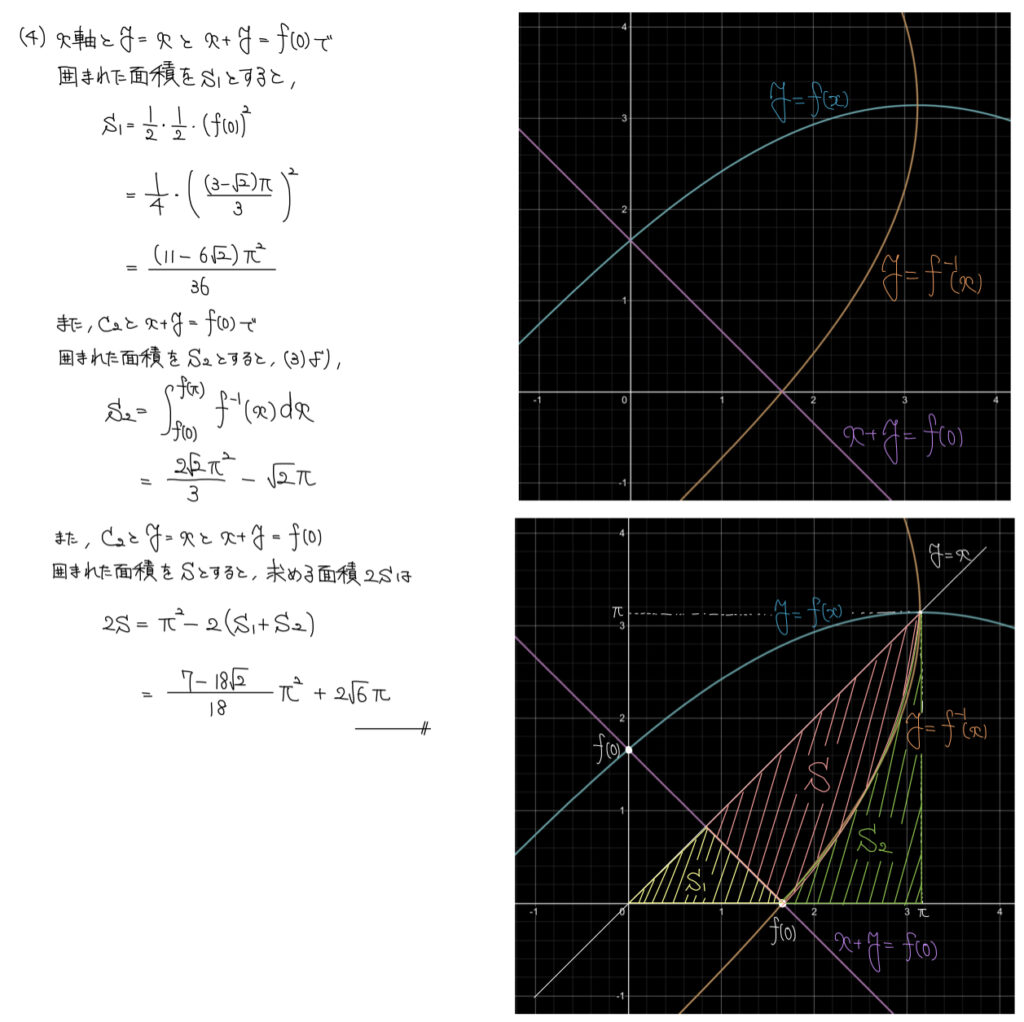
解説
まず図示をしてどこを示すのかを明らかにしよう。
よく分からない形の面積は求める部分のみ求めて、足したり引いたりすることで求めたいところを求めることを考えよう。
今回も値の計算が少しだけ面倒ではあるが、全体から余分な部分を引いて求めにいく。
図を丁寧めに描いたつもりなのでイメージを掴むために参考にしていただきたい。
さいごに
公式の模範解答はこちら
https://www.kanazawa-u.ac.jp/wp-content/uploads/2020/04/02-2-02sugaku_rikei_zenki.pdf
参考URL:国立大学法人金沢大学HP 『過去問題及び正解・解答例』より令和2年度 前期日程 数学(理系) 正解・解答例
問題の難易度は、私立で言えばGMARCHレベルと比べても少し難しいように思う。
個人的には(4)を解く際の(3)の利用が好きだ。
単純と言えば単純な利用ではあるが、逆関数というだけで自分にとっては(おぉ〜)となってしまった。
おそらく自分が受験生の時は解けない問題であった。
(2)まで解いたら飛ばして、大問3に注力しただろう。
どこを解くべきか、どこを解かないべきか、見極められるようになろう。
受験まで期日的に余裕がある人はしっかり復習して力にしていこう。



コメント