2020年度日本大学の過去問を解いたので解答・解説をしていく。
2020年度N方式の全ての問題を解き、文系が大問1〜4、理系が大問5〜10であることには注意してもらいたい。
それでは、早速見ていこう。
問題(大問1)

まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
日本大学は偏差値35.0〜67.5の私立大学(2021年7月7日時点 パスナビ調べ)。
偏差値自体は35.0の工学部から67.5の医学部まで幅広いため、あまり偏差値はあまり参考にならない。
教科書レベルの基本的な問題だ。
単元も様々で、広く基本的なことができることが問われる。
GMARCH以上や中堅国立を志望する人は基礎力を定着させるためにもしっかり完答できるようにしておこう。
(1)2次関数の最大・最小
解答

解説
定義域内の最小値についての問題。
二次関数の最大・最小問題は迷わず
- 平方完成して
- 頂点確認して
- 簡単なグラフをかく
という手順でいこう。
今回は軸が文字定数のため、軸が定義域の
- 左側
- 内側
- 右側
でそれぞれ場合分けを考えよう。
あとはそれぞれの場合の最小値を考えて、合わせてあげればよい。
(2)対数方程式
解答
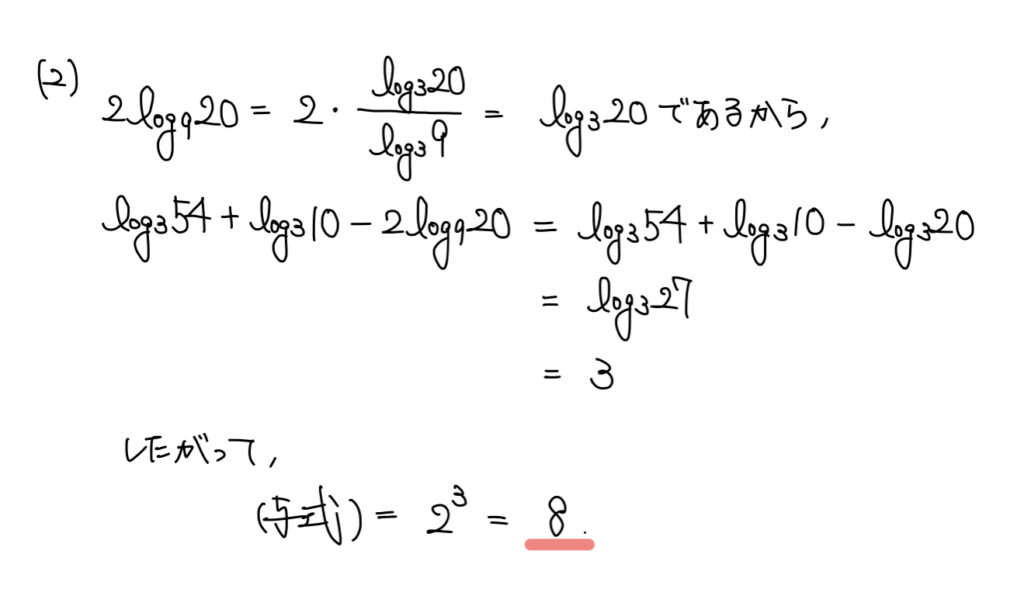
解説
対数方程式ではまず
- 底aの範囲(0<a<1,a≠1)
- 真数条件
に注意するのが鉄則だ。
今回は底や真数に文字がないため、考えなくてよい。
対数の足し算・引き算を行うにあたって、まずは底の統一をしよう。
底が統一できたら、あとは足し算・引き算を行いながら対数がなくなる形に変形していこう。
(3)数列の和
解答
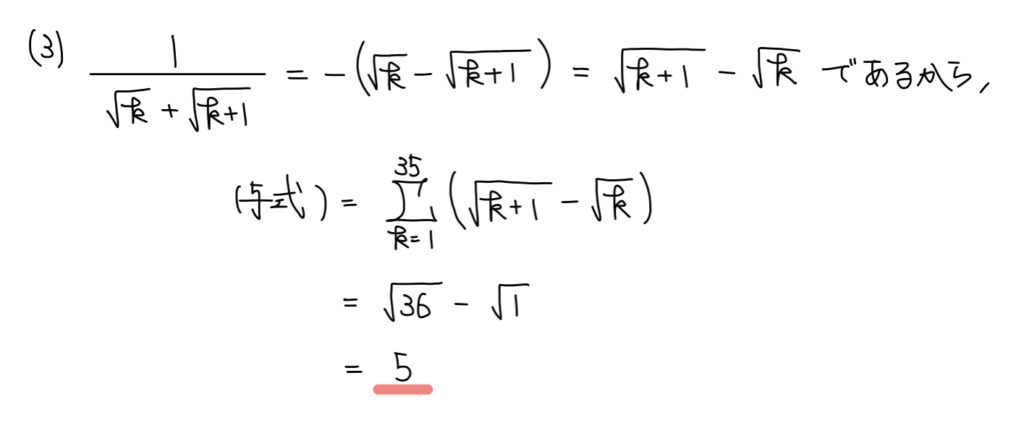
解説
Σ計算が素直に出来ない形は工夫か具体化を考えよう。
今回は無理式の分数式であるため、有理化を考えよう。
有理化すると各項ごとに相殺する項が出てくるため、計算がかなり楽になる。
極限や数列の和では有理化が有効な場面も多いため、しっかり頭の片隅には置いておこう。
(4)直線の方程式
解答

解説
これは基礎レベルであればどの問題集にも書いてあるような有名な問題だ。
まず、求めたい座標を文字で置こう。
この際に変域があれば必ず確認しよう。
その後は
- 中点が対称軸上
- 対象軸と対称な線分が直交 → 傾きの積が−1
で解ける。方針が見えていればあとはその通りにペンを動かすだけだ。
さいごに
大問1に関しては立ち位置としては文系の基礎事項チェックというところだろうか。
どれも基礎的な問題集に載っているような難易度だ。
出来なかったところはしっかりできるようにしておこう。
簡単とはいえ、様々な分野から出題されるため、基礎事項の抜けがないようにしておこう。



コメント