2020年度日本大学の過去問を解いたので解答・解説をしていく。
2020年度N方式の全ての問題を解き、文系が大問1〜4、理系が大問5〜10であることには注意してもらいたい。
それでは、早速見ていこう。
問題(大問2)
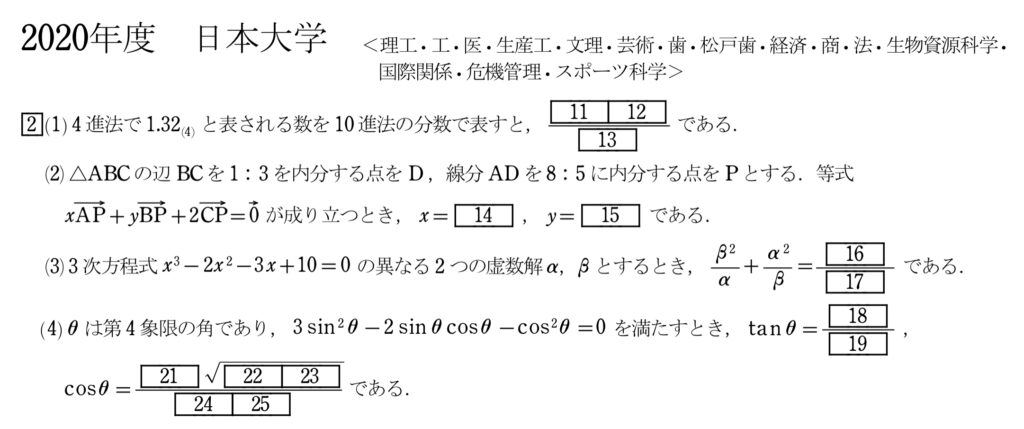
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
日本大学は偏差値35.0〜67.5の私立大学(2021年7月7日時点 パスナビ調べ)。
偏差値自体は35.0の工学部から67.5の医学部まで幅広いため、あまり偏差値はあまり参考にならない。
教科書レベルの基本的な問題だ。
単元も様々で、広く基本的なことができることが問われる。
GMARCH以上や中堅国立を志望する人は基礎力を定着させるためにもしっかり完答できるようにしておこう。
(1)n進法から10進法への変換
解答

解説
今回は4進法から10進法への変換だ。
n進法は各位に注目すればよい。
具体的には次の通りだ。

今回40の位が1、4-1の位が3、4-2の位が2であるからそれを計算すればよい。
(2)平面の位置ベクトル
解答

解説
この場でだけベクトルの実数倍を「係数」と言い方をする。(イメージを掴みやすいため、正確には実数倍というのがよい)
同じベクトルの表記が2通りあれば係数比較すればよい。
ただし、基準とした2つのベクトルが一次独立である確認は必ずすること。
ACベクトルの係数が2で一致しているため、その他のベクトルの係数を比較すれば求めることができる。
(3)因数定理、対称式
解答

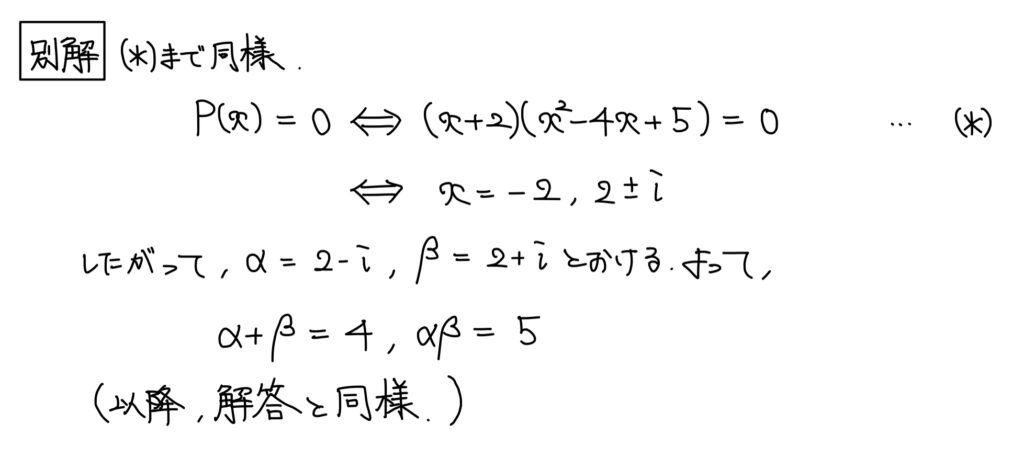
解説
考察対象が虚数解α、βのため、α、βを調べるためにまず3次方程式を解くことから始める。
3次以上の整関数の方程式(高次方程式)の解法は以下の通り。
- 因数定理・乗法公式(複2次式)を用いて因数分解
- 「ABC=0」ならば「A=0 または B=0 または C=0」の利用
α、βは虚数解よりx2-4x+5=0の2解。
ここからα、βを求めにいっても良い(別解)が、求める形が対称式であるから、α、βの基本対称式(α+β、αβ)さえ求めれば良い。
そういった考えから、解と係数の関係で基本対称式を得ればよい。
あとは、対称式を基本対称式を用いれる形に式変形していけば良い。
分数式の加法・減法は通分。
(4)三角関数・三角方程式
解答

解説
2次の三角方程式を解くためには
- 次数下げして合成
- t=sin+cosとおいて置換
というのが定石。
ただし、今回は「θの値を求めよ」のような問題ではなく、聞いているのはあくまでtanの値。
ゆえに、tanが現れるような式変形を考えると「cosの2乗で割る」という発想が出てくる
tanが現れたらあとはそれを求めれば良い。
また、三角比は一つ求めることができれば残りの二つは相互関係から導ける。
cosは三角比の相互関係を用いて求めよう。
さいごに
基礎的でありながらも抜けてそうな知識を解いてくる良い問題だと思う。
というのも
- n進数は整数部分の中でも多くの受験生があまり力を注がない単元であるし、
- 位置ベクトルも交点の位置ベクトルや同一直線上ほど頻出でない式変形、
- 複素数も2次関数ではなく3次関数にすることでひと手間追加されていて、
- 2次の三角方程式もθではなくtan求め、かつ三角比の相互関係も一番扱う機会が少ないtanとcosの相互関係
だ。
問題自体の難易度は標準的であるが、広い範囲まで網羅できているかというところが問われているように思う。
これを機に忘れていた単元を復習できれば筆者冥利に尽きる。
これからも楽しんでいこう。



コメント