2020年度日本大学の過去問を解いたので解答・解説をしていく。
2020年度N方式の全ての問題を解き、文系が大問1〜4、理系が大問5〜10であることには注意してもらいたい。
それでは、早速見ていこう。
問題(大問3)
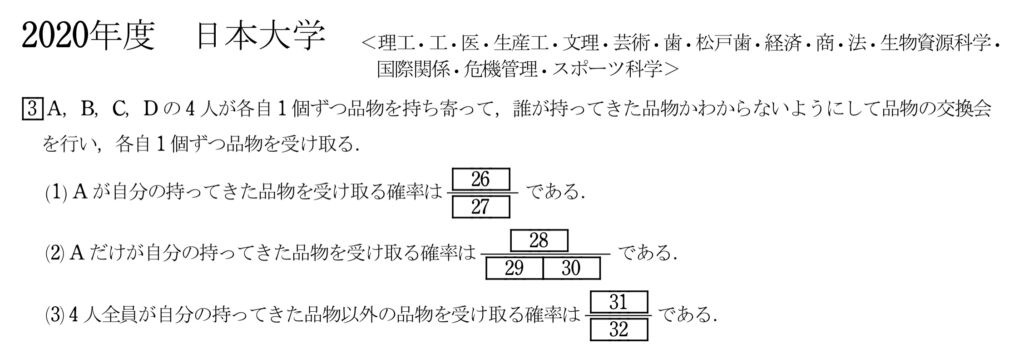
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
日本大学は偏差値35.0〜67.5の私立大学(2021年7月7日時点 パスナビ調べ)。
偏差値自体は35.0の工学部から67.5の医学部まで幅広いため、あまり偏差値はあまり参考にならない。
教科書レベルの基本的な問題だ。
単元も様々で、広く基本的なことができることが問われる。
GMARCH以上や中堅国立を志望する人は基礎力を定着させるためにもしっかり完答できるようにしておこう。
(1)確率
解答

解説
確率や場合の数のよくある発想として限定されたものから考えるということがある。
今回で言えば「Aは自分のものを受け取る」というのが唯一の限定だ。(B、C、Dは何を受け取ってもよいため状況が限定されていない)
ゆえに、Aをどう扱うかだけ先に考える。
Aは自分のものを受け取らなければいけないわけだから、Aが品物を受け取る場合の数は自分のもののみの1通り。
他3人は何を受け取っても良いため3人を並べる順列を考えれば良い。
(2)確率
解答
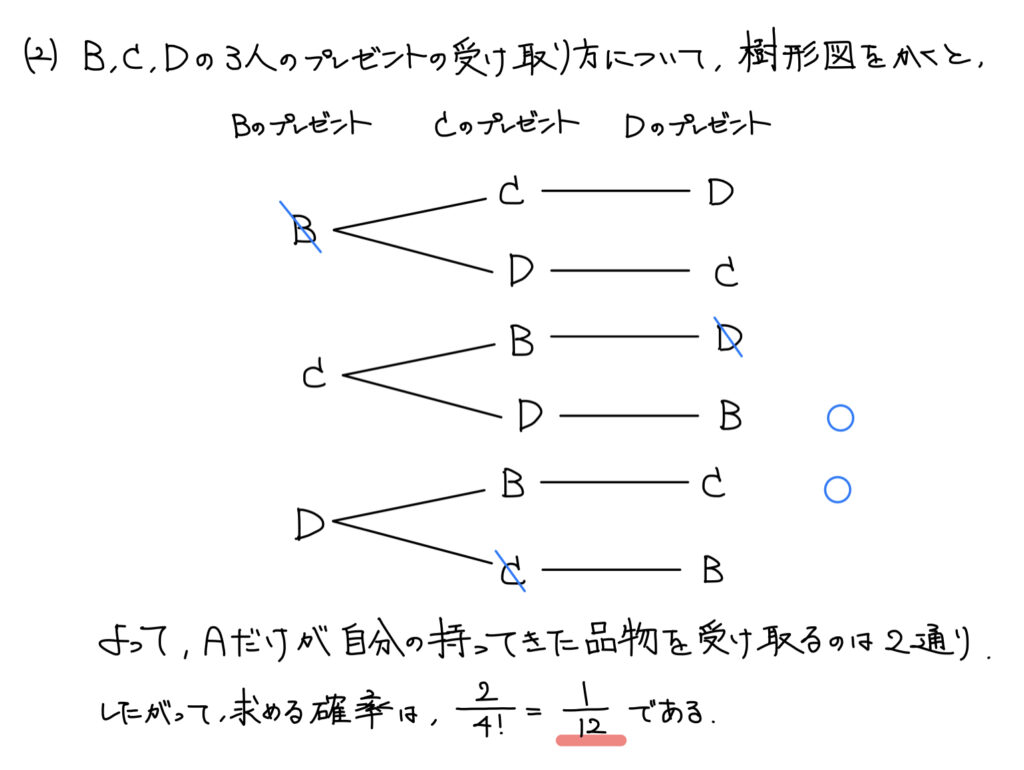
解説
限定されたものから考えるというのは(1)同様。
しかし、「Aだけが自分の品物を受け取る」という条件から「Aだけ限定されている」と考えるのは誤り。
B、C、Dも「自分自身の品物を受け取ってはいけない」という限定が起きていることに注意しよう。
では、どうしようと悩んでしまうわけだが、分からない時は状況を具体化して把握しよう。
具体化するために樹形図を用いると直ちに把握できて解くことができる。
(3)余事象の確率
解答
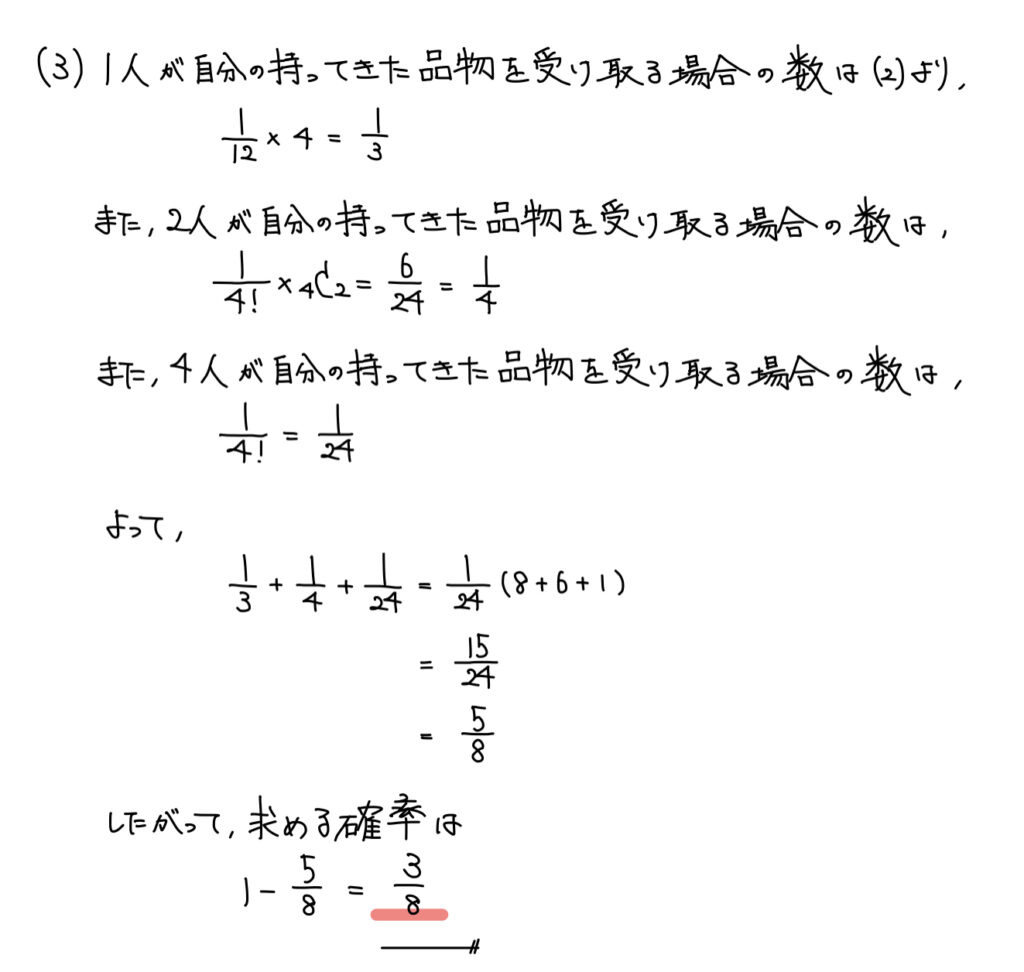
解説
最終問題にして「Aが」という条件がなくなったが、(1)、(2)の流れから同様に考えていけば良い。
正直、今回は全ての場合の数が高々24通りであるから、樹形図で全体を把握すれば直ちに解ける。
もし試験本番で自分がこの問題を受けるとなったら樹形図で解くだろう。
解答は別の方法を紹介していく。
「全員自分のものでない」という状況が「少なくとも1人以上自分の品物を受け取る」の余事象関係ということを考える。
「少なくとも1人以上自分の品物を受け取る」というのは(1)、(2)の流れから考えよう。
さいごに
確率をサッと学んだ受験生の多くに「P、C、!を使って解きたい」というのがあるだろう。
ゆえに、今回のような樹形図や表を用いた問題で悩む人は多いと思う。
確率の単元に限らず、悩んだら具体化・実験というのは常に念頭においておこう。
これからも楽しみながら解いていこう。



コメント