ベクトルの問題について扱う「ベクトル道場」シリーズ。
今回解いたのは「2020年度 東京海洋大学(前期入試:海洋工) 大問3」だ。
難易度目安【易 ★★☆☆☆ 難】
では見ていこう。
問題

まずは解説より先に問題を解いてもらいたい。
分からなかった人は解説を見てもらって、方針を参考にした上でどこから解けていないかを炙り出してもらえれば嬉しい。
では、問題解くの頑張って!
〜答案作成中〜
お疲れ様でした。
それでは、解答解説を始めていこう。
概評
ベクトルは本来必要な図さえ書き出せば、全ての形を把握する必要はない。
図形の全体像を把握しなくても式処理で解ける、すなわち、図形問題を図形をかくことなく数式で処理できるというのがベクトルの凄いところだ。
そういったことから今回は作図せずに解いてみた。(単純に自分が解いた際に作図が必要ないと感じてしなかっただけだが)
分かりづらい点があったら申し訳ないが、今回はそんな式処理で解けるベクトルの凄さを感じてもらえれば嬉しい。
ご自身で解く際にあまりにもイメージがしづらければ作図してイメージを掴んでもらいたい。
ちなみに、今回作図をせずに解けると思った理由としては、角度や辺の長さの情報が十分に揃っていたからだ。
もっと情報が少なく、作図しなければ見えてこない状況であれば作図をするが、今回は十分なほどに情報があるため、作図はいらないと判断したためだ。
前置きが長くなってしまったが、それでは、一問一問楽しみながら見ていこう。
(1)空間の位置ベクトル
解答
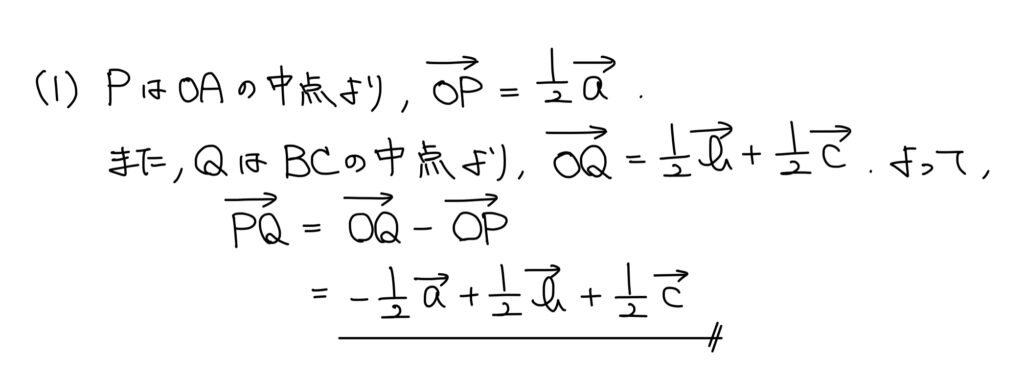
解説
Oを始点とする位置ベクトルを考える。
まずPQベクトルの始点をOへと変更する。
するとOPベクトルとOQベクトルを求めれば良いことが分かるため、それぞれを求めにいく。
Pの位置はOから見てAまでの半分の地点、Qの位置はBCの中点より位置ベクトルが分かり求めることができる。
(2)ベクトルの大きさ、内積
解答

解説
(1)でPQベクトルを求めているのでそれを利用する。
大きさは内積や長さが出てくるため、必要なものを先に準備しておき、準備が終えたら内積の性質を用いて調べれば良い。
2次関数の最大・最小問題は「平方完成して簡単なグラフをかく」ことで視覚的に解ける。(今回は定義域が実数全体なため、頂点が最小値と直ちに分かるためグラフを省略した)
(3)ベクトルのなす角
解答

解説
「ベクトルでなす角」と言われたら迷わず内積から攻めたい。
今回は角度を求める問題ではなく、cosを求める問題ではあるが、思考は全く同様。
必要なのは内積と大きさだ。
内積と大きさで分からないものは調べれば良い。
(4)三角形の面積
解答

解説
ベクトルで面積と言われたら「内積」か「成分」の公式を考えるわけだが、(3)で三角形の面積の一つの角のcosで求められていることから「2辺と間のsin」でも良いだろう。
もちろん、内積で求めることもできるが、今までのベクトルの大きさを求める流れから考えても今回は「2辺と間のsin」で求めることが有効だろう。(明らかに成分では求められない)
三角比の相互関係を用いて、cosからsinの値を導き、あとは2辺を求めれば良い。
三角形の面積と言われたら
- 底辺と高さ
- 2辺と間のsin
- 座標(ベクトルの成分)
- 内積
- 内接円
のいずれかを考えるという発想は持っておこう。
他にも外接円やヘロンの公式もあることはあるが、受験数学においてそれらを考えなくては解けないという場面はまずない。
しっかり以上5パターンを把握しておこう。
さいごに
難易度は高くなかったが、誘導の流れは個人的に分かりやすくて好きな問題であった。
誘導に気付く訓練が足りていない学生にはとても有効な問題のように思う。
逆に、すんなり誘導に乗れる人は前問との繋がりを意識的に見えているのでとても良いのではないだろうか。
自分ももっと難しい問題の誘導も見破られるようになりたい。
何か解答不備などあったらコメントで教えてもらえればありがたいです。
一緒に頑張っていこう。
※無断転載や商業目的の利用は控えていただきますようお願いします。



コメント