2020年度神戸大学の過去問を解いたので解答・解説をしていく。
今回は前期日程(理科系)の問題を解いた。
文科系の問題ではないことには注意してもらいたい。
それでは、早速見ていこう。
問題
以下のURLは大学の公式HPから入試問題へのリンク。
問題はそちらから確認して欲しい。
URLからのリンクが怖い方は『神戸大学 過去問』で検索してみて欲しい。
目安時間:22分
2020年度 神戸大学 前期日程 数学
[ https://www.office.kobe-u.ac.jp/stdnt-examinavi/wp-content/uploads/2020/08/03.suugaku_rikei.pdf ]
※上記URL:国立大学法人神戸大学HPホーム > 入試情報 > 学部入学案内 >入試問題及び出題の意図など > 2020年度一般入試(入試問題/出題の意図・評価ポイント/解答例)> 前期日程 数学 理科系 問題
※過去4年分が公式HP(下記URL)から閲覧できます。(2021年8月29日時点)
※掲載終了している可能性もあります。
参考URL『国立大学法人神戸大学HP>入試情報>学部入学案内>入試問題及び出題の意図など』
https://www.kobe-u.ac.jp/admission/undergrad/examin/index.html
まず、実際に解いてみて欲しい。
頑張って。
解けたでしょうか?
それでは解答解説をしていこう。
解答・解説
概評
神戸大学は偏差値55.0〜67.5の国立大学(2021年8月30日時点 パスナビ調べ)。
大問2は軌跡と回転体の体積についての問題だ。
難易度はGMARCHレベルの問題だ。
(1)は座標を与えられている上で示せばいいため、普通の軌跡の問題より答え合わせができるという点で簡単になっている。
(2)については媒介変数表示というのが受験生を苦しめるポイントになりそうだ。
小問2つのためそれぞれ時間をかけられるが、計算の分量がそこそこあるため油断せずに解いていきたい。
それでは解答を見ていこう。
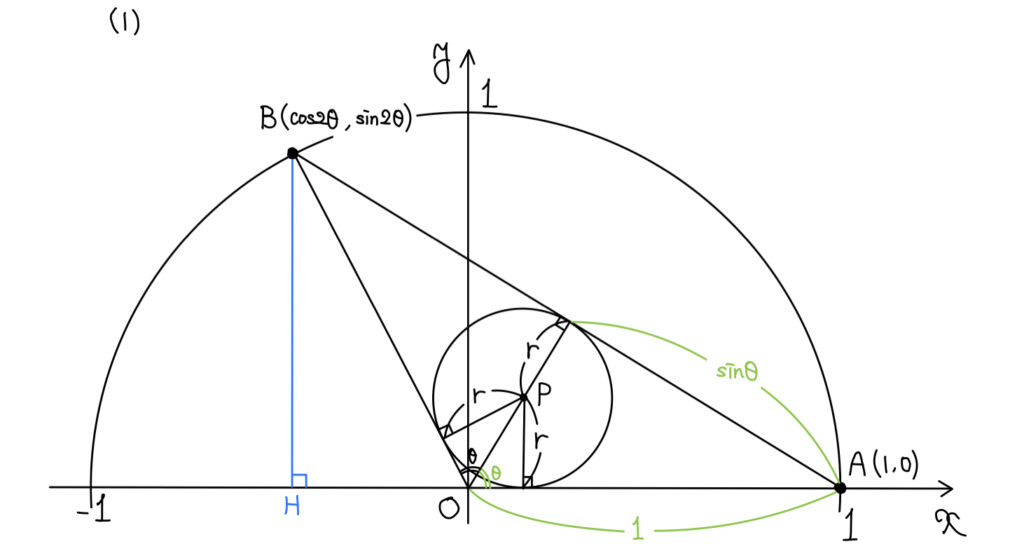
(1)座標の軌跡
解答


解説
軌跡の問題で鉄板の解法が
P(X,Y)とおいて媒介変数の存在条件を求める
というものだ。
今回もこの方針でいいだろう。
まず、「座標と三角比」というところから単位円を考えたい。
これができないと今回は厳しそうだ。
その後、「三角形の内心」というところからすぐに
- 角の2等分線の交点
- 面積での利用
の方針は立てたい。
辺の長さや角度からPを表しに行きたいため、Pの座標はどうしたら求められるかなという発想は常に持っていなければいけない。
そこで今回は最後に書いているがP(X,Y)とおいた最後の媒介変数表示が見えている。
ゆえに話は「内接円の半径を求ればいい」という話に言い換えることができる。
あとは内接円と半径というところから面積を考えて解答を得る。
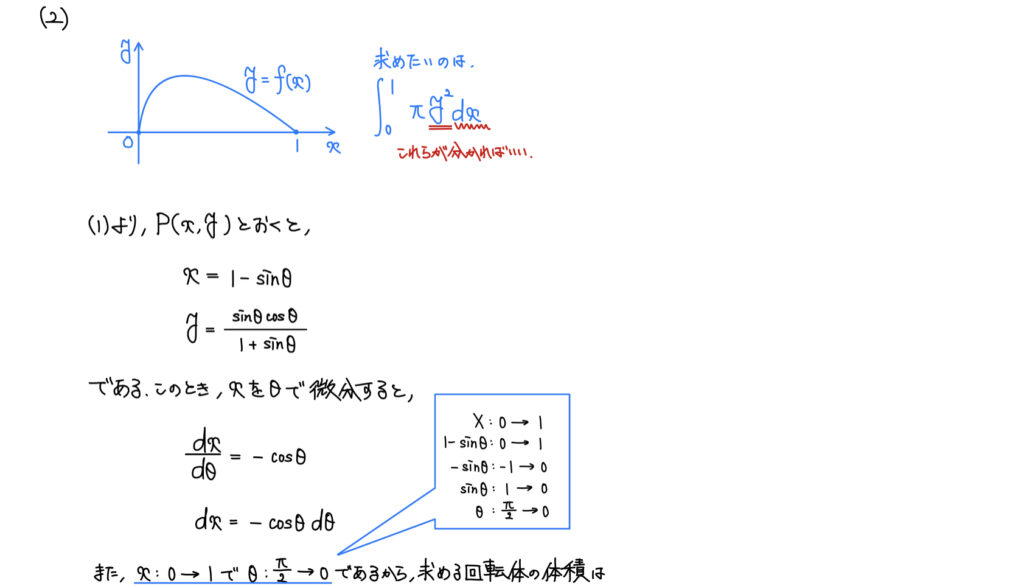
(2)回転体の体積
解答

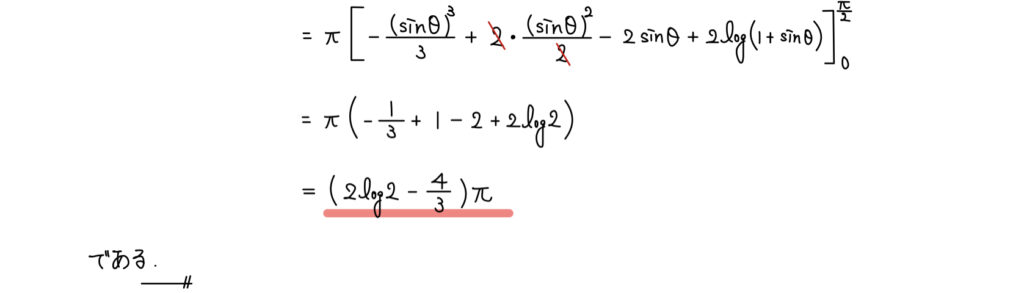
解説
媒介変数表示で厄介!と思った人もいるかと思うが、こういう時こそ基本に立ち返ろう。
求めたいものを見ると結局知りたいのはy2とdxであることが分かり、これらを知るためには(1)の結果を使えばいいということが分かる。
そこから先は計算あるのみだ。
解答ではかなり丁寧に途中式を書いた。
解答としては冗長であるため、入試本番は計算用紙に計算し、もっと省略した解答を書こう。
さいごに
今回の問題はシンプルではあるが誰しもが正答できるとは言いにくい問題であるように思う。
一方で、考え方は基本通りで方針も見えやすい。
基本事項をちゃんと引き出せるか、というところが問われているように思う。
個人的にはこういった問題は好きであるため、解いていて楽しかった。
解いた方お疲れ様でした。
これからも一緒に頑張っていきましょう。
その他過去問を解く人はこちらから → 『特集 過去問振り返り まとめ』
本ブログの解答解説は大学が公式に発表しているものではなく、あくまでブログ著者が独自に執筆した解答であることをご了承ください。 尚、解答解説の作成・公表にあたり十分に注意をしておりますが、万が一解答に誤りがあった場合にも責任は負いかねます。 コメントいただければ確認、修正致します。 何卒よろしくお願い致します。



コメント